8阶上三角幂零矩阵在上三角变换下的Belitskii标准形
2023-09-07张恩萍刘星月王一帆
张恩萍,刘星月,王一帆
(1.湖北大学楚才学院, 湖北 武汉 430062; 2.湖北大学数学与统计学学院,湖北 武汉 430062;3.湖北大学计算机与信息工程学院, 湖北 武汉 430062)
0 引言
矩阵的相似分类问题是线性代数的核心问题之一,Jordan标准形与Frobenius标准形定理是线性代数最重要的定理,也是线性代数发展完善的重要标志.然而,在实际应用中的很多矩阵问题,往往是某些矩阵的集合在某些允许变换下的相似问题,例如著名的Rojter问题[1].2000年,Sergeichuk引入了一类线性矩阵问题(Λ,M),利用分块矩阵的方法,描述了某些矩阵的集合M在一定的允许变换Λ下的相似问题,并利用Belitskii约化算法,给出了约化矩阵相似标准形的方法[2].偏序集、箭图和有限维代数的表示分类问题都可以看作是线性矩阵问题的特例.
线性矩阵问题的核心问题之一是确定它的表示型.如果线性矩阵问题 (Λ,M)只有有限个不可分解表示的同构类(或相似类),则(Λ,M)称为有限表示型;如果对任一正整数n,(Λ,M)的阶数为n的不可分解表示可由有限多个单参数簇来表示,则(Λ,M)称为可驯表示型;如果存在某个正整数n,(Λ,M)的阶数为n的不可分解表示至少需要2个或2个以上的参数簇来表示,则(Λ,M)称为野表示型[2-3].
上三角幂零矩阵Mn在上三角可逆变换Λn下的相似分类问题是一类重要的线性矩阵问题.Damjan Kobal利用Belitskii算法计算了阶数小于等于5的上三角幂零矩阵在上三角变换下的相似标准形,给出了低阶上三角幂零矩阵在上三角变换下的相似分类[4].P.Thijsse利用矩阵扩张的方法得到了阶数至多为6的上三角幂零矩阵在上三角变换下的不可分解相似类[5].进一步地,Chen等[6]证明当n≤5时,(Λ,M)是有限表示型;当n=6,7时,(Λ,M)是可驯表示型;而当n≥8时,(Λn,Mn)是野表示型,该文中也计算了n=6,7时的不可分解矩阵的相似标准形.由于野表示型的分类问题被公认为是没有希望的,所以阶数大于等于8的上三角幂零矩阵在上三角变换下的相似标准形尚少计算.
野表示型的表示范畴是非常复杂的,需要依赖多参数簇来表示.利用代数几何及变换群的语言定义的参数μ(indM)是用来度量线性矩阵问题的不可分解矩阵范畴复杂性的较为精确的方式之一[7-8].刘先平等[8]的结果表明参数μ(indM)等于(Λ,M)的不可分解矩阵标准形中所含参数个数的最大值.因此,通过计算当n≥8时(Λn,Mn)的不可分解矩阵标准形来探索野表示型的上三角幂零矩阵问题的复杂性是一种新的尝试.
本研究创新性地对Belitskii约化算法进行编程,利用计算机计算n=8时 (Λn,Mn)的所有不可分解相似标准形,其中有333个标准形不含参数,有65个标准形仅含1个参数,有4个标准形含2个参数.
1 Belitskii算法及其程序
设n阶上三角幂零矩阵的集合Mn={(aij)n×n|aij=0,i≥j},以及n阶上三角矩阵变换群
Λn={S=(sij)n×n|sij=0,i≥j;sii≠0,1≤i≤n},
则群作用
Λn×Mn→Mn,(S,A)|→S-1AS
(1)
定义了线性矩阵问题(Λn,Mn).Belitskii构造的约化算法对任一给定的矩阵A∈Mn,都存在可逆矩阵S∈Λn,使得S-1AS=A′的上三角元素只能为0,1或是参数λ,称为矩阵A的Λ- 相似标准形,或A的Belitskii标准形.
1.1 Belitskii 算法我们回顾一下Belitskii的约化算法,详见文献[2,6].首先对Mn中的矩阵A=(aij)n×n的上三角元素按照由下至上,由左至右的顺序进行排序,即
aijai′j′⟺i>i′,或i=i′,j (2) (3) (4) (5) 重复以上过程,我们可以得到一个约化序列 (Λn,Mn)=(Λ(0),M(0)),(Λ(1),M(1)),…,(Λ(s),M(s)), 其中,M(s)中的矩阵所有的上三角元素均被约化,称为Belitskii标准形. 1.2 程序实现本节将用Python对Belitskii算法进行编程,编程步骤如下: 1)初始化矩阵:对于三类上三角矩阵:待约化矩阵A、变换矩阵S、相似矩阵A′,分别初始化为a_ij、s_ij、a′_ij的格式,用于后续提取. 2)矩阵的DFS遍历:以"+"号为分隔符,等式两边均只有1项时,为边约化或圈约化,反之为正则化.且s_ij下标相等为边约化,反之为圈约化.特别地,若左右两式下标一致,则为参数形式. 按照既定顺序,通过矩阵乘法逐项列式,定义如下规则: ①对于a_ij=0,对应的a′_ij赋值为0. ②对于边约化,对应的a′_ij赋值为1,并对原矩阵进行深拷贝.此时S需要更新,优先修改既定顺序中后出现的元素.通过DFS遍历下一个元素,并对矩阵进行回溯,到达最后一个元素的位置时,结束遍历. ③对于圈约化,a′_ij赋值为λ,S不做更新.其余流程与边约化同. 3)打印矩阵:定义参数count_1用于储存边约化的1的个数,参数flag用于判断是否可以打印.对矩阵进行DFS遍历,若矩阵A′中出现一次1,则count_1+1,若count_1=flag将矩阵存储在列表中.在扫描过程中,若矩阵A′中的某元素为λ,说明是含参矩阵,直接添加至列表中.最后打印列表并去重. 设k是一个代数闭域.记Mn=Mn(k)为k上n×n上三角幂零矩阵的集合.集合Λn为k上n×n上三角可逆矩阵的全体.对于任何A,B∈Mn,如果存在S∈Λn使得B=S-1AS,则称A和B是Λn-相似的.每个相似类,都有一个“最好的”代表元,称为相似标准形.在本文中,我们计算了n=8的所有不可分解的Belitskii标准形. 为简单起见,本文中仅列出n=8的情况下,且至少包含两个参数的不可分解标准形,定理如下. 定理设(Λ8,M8)是由8阶上三角幂零矩阵关于上三角可逆变换组成的线性矩阵问题,则(Λ8,M8)中至少包含两个参数的不可分解Belitskii标准形只有以下4种形式: 其中,λ、μ∈k为二个参数. 定理的证明我们仅证明第一个矩阵是含两个参数的不可分解Belitskii标准形,其余3个可类似证明.下面使用1.1中的算法对其约化. 令Α为第一个上三角矩阵,变换矩阵S∈Λ8. 为保持a′78在后续约化中不变,构造子群Λ(1): Λ(1)={S=(sij)∈Λ8|s77=s88}, 接下来约化Λ的a67,a68,……如此连续,假设已约化至元素a28,约化结果如下: Λ(21)={S=(sij)∈Λ(20)|满足下面的条件式(6)}, 其中,条件式(6)为 (6) 类似地,继续计算A中剩余所有未约化项,均为正则化,记为∅.最后,我们得到了A的含两个参数的标准形(第一种标准形式): 其中,λ、μ∈k为参数.显然,J(λ,μ)中包含7个边约化值1,故为不可分解标准形.同时A的变换群为: Λ(28)={S=(sij)∈Λ(27)|满足条件(6)与下面的条件(7)}, 其中,条件(7)为 (7) 同理,通过计算机遍历所有上三角幂零矩阵,从而得到至少含两个参数的不可分解标准形全体,仅有定理中的四类形式. 证毕. 上述定理表明,(Λ8,M8)中仅含有4个2-参数化的Λ8-相似类.计算机结果进一步表明(Λ8,M8)共有402个不可分解矩阵标准形.其中333个标准形不含参数,有65个标准形仅含1个参数,有4个标准形含2个参数.可见,野表示型的表示范畴多而复杂,不仅需要依赖多参数簇来表示,不可分解矩阵的相似分类的复杂性也远高于有限与可驯表示型. 上述计算结果表明,上三角幂零矩阵问题(Λ8,M8)的不可分解标准形中至多含2个参数,由文献[8,定理3.2]可得: 推论μ(Λ8,M8)=2. 致谢感谢徐运阁教授的悉心指导.
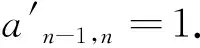


2 主要定理




