实对称矩阵标准形的一些应用
2023-09-07刘合国廖军
刘合国,廖军
(1.海南大学数学系, 海南 海口 570228; 2.湖北大学数学与统计学学院, 湖北 武汉 430062)
0 引言
矩阵和线性变换的标准形理论是矩阵代数的精华,更是高等代数(线性代数)里最重要的核心内容.熟练地运用标准形的思想去解决矩阵和线性变换的各类问题,是学生学习高等代数(线性代数)这门课程必须具备的能力.进一步地,这种由繁入简的标准形思想也在几何学、分析学、统计学等学科里发挥着基本作用.
在一个代数闭域上,每个n阶矩阵A都相似于它的Jordan标准形.即存在可逆矩阵P,使
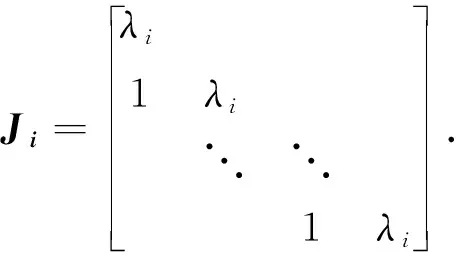
这是众所周知的Jordan标准形定理,例如见文献[1,定理8.10,定理8.11]或文献[2].在一个一般的域上,设n阶矩阵A的非平凡的不变因子为I1(λ),I2(λ),…,It(λ),则存在可逆矩阵P,使
这里Fi是多项式Ii(λ)的友矩阵.这就是我们通常所说的矩阵有理标准形(Frobenius标准形)定理,例题可见文献[1-2].
其实,有理标准形定理是可以细化的.精确化之后,我们可以看到矩阵的有理标准形定理完整地包含了Jordan标准形定理,下面的有理标准形定理是矩阵代数里最深刻的内容之一,见文献[3].
设A是域F上的n阶矩阵,它的特征多项式为
ΔA(λ)=|λI-A|=I1(λ)I2(λ)…It(λ),
其中Ii(λ)(1≤i≤t)是A的非平凡的不变因子.进一步,设
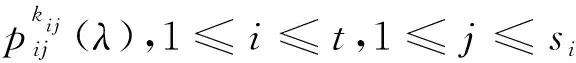
设Pij是pij(λ)的友矩阵,设lij=degpij(λ),设Nij为只有(1,lij)位置为1,其他位置全为0的lij阶方阵,称块矩阵
为初等因子pij(λ)kij对应的Frobenius块矩阵.特别地,当pij(λ)=λ-λij时,
为Jordan块矩阵.
矩阵的Frobenius有理标准形定理叙述为:域F上的n阶方阵A相似于Frobenius块对角矩阵
diag(C11,…,C1s1,…,Ct1,…,Ctst),

diag(J11,…,J1s1,…,Jt1,…,Jtst),

从矩阵的Jordan标准形和有理标准形的角度看,
是两类极其重要的矩阵,在理论和应用上都具有基本的重要性.
实对称矩阵和正交矩阵是高等代数(线性代数)里的另两类重要矩阵,一般地,这两类实矩阵的结论可以平行地推广到复数域上的Hermite矩阵和酉矩阵.下面的定理对理解实对称矩阵和正交矩阵是非常关键的.
定理1([1,定理5.2,定理5.5,定理9.7]) 设A是n阶实对称矩阵,则存在正交矩阵Q,使得
式中,λ1,λ2,…,λn是A的特征值.
定理1是处理实对称矩阵和实二次型的有力工具,如果记Q=(α1,α2,…,αn),那么可得

结合惯性定理,我们不难看出实二次型XTAX的正(负)惯性指数等于A的正(负)特征值的个数.
定理2设O是n阶正交矩阵,则存在n阶正交矩阵Q,使得

本研究目的是给出这些标准形定理(特别是定理1)的一些应用,它们对理解这些基本定理是有帮助的.文中涉及到的知识可见文献[1-2].
1 樊畿不等式
下面的不等式是Wirtinger不等式的离散模拟,曾被某些高校用作高等代数(线性代数)的考研试题.如下的证明是阐明用矩阵标准形来解决问题的极佳范例.
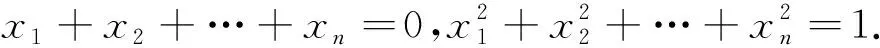
设f(x1,x2,…,xn)=x1x2+x2x3+…+xn-1xn+xnx1,容易看到
f(x1,x2,…,xn)=x1x2+x2x3+…+xn-1xn+xnx1
令
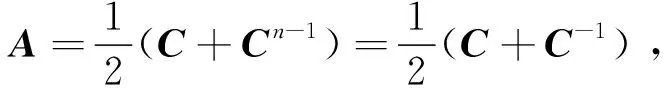
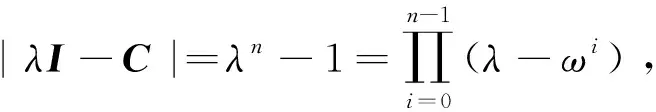
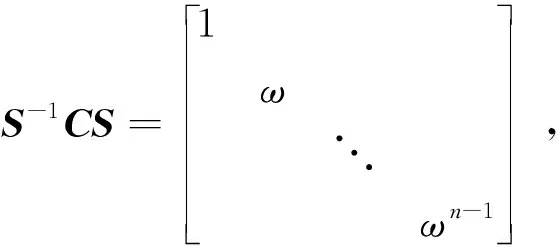
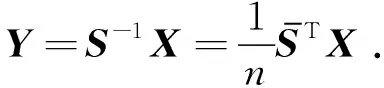
注1在上述证明里出现的矩阵
就是有名的Schur矩阵,它在有限Fourier变换里起着基本的作用.这个证明也可以用有限Fourier变换的语言改写出来.
事实上,对n个复数y1,y2,…,yn,定义
此时亦有



当n为偶数时,

当n为奇数时,

令X=QY,则Y=QTX.注意到这里Q的第一列是属于特征值1的单位特征向量,因此其各分量相等,从而y1=0.而且YTY=XTQQTX=XTX=1.所以,
f(x1,x2,…,xn)=XTCX=XTAX=YTQTAQY
证法三(运用定理2) 利用正交矩阵的正交相似标准形.由于CTC=I.Cξi=ωiξi,i=0,1,2,…,n-1,存在正交矩阵Q,使得
当n为偶数时,

当n为奇数时,

令X=QY,则Y=QTX.注意到这里Q的第一列是属于特征值1的单位特征向量,因此其各分量相等,从而y1=0.而且YTY=XTQQTX=XTX=1.所以,
f(x1,x2,…,xn)=XTCX=YTQTCQY
2 定理1的两个证明
我们在文献[4]里利用分析学的结果给出了定理1的一种存在性证明,它也可以用另外两种形式表达出来.
证法一先证明一个已知的简单事实:设B是n阶实对称半正定矩阵,则
{X∈n|XTBX=0}={X∈n|BX=0}.
其实,只需证明{X∈n|XTBX=0}⊆{X∈n|BX=0}.因B是半正定的,存在可逆变换X=PY,其中Y=(y1,y2,…,yn)T,使
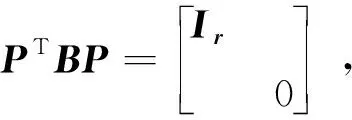
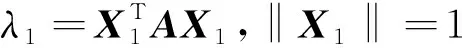


断言对2≤i≤n,b1i=bi1=0,事实上,对n里的单位向量
Xθ=X1cosθ+Xisinθ=Q1(e1cosθ+eisinθ),


3 定理1的应用
例2设Ai,i∈I是一簇两两交换的n阶实对称矩阵,证明存在正交阵Q,使得对每个i∈I,QTAiQ是对角矩阵.
证对n进行归纳.如果每个Ai(i∈I)都是实对角阵.取Q=I即可.假设某个Ai不是对角的,由定理1知存在正交矩阵P,使得
对任意的j∈I,PTAjP仍然是实对称矩阵.由于AiAj=AjAi,则(PTAiP)(PTAjP)=(PTAjP)(PTAiP),因此PTAjP是块对角矩阵.设
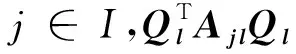
例3设A实对称,半正定,对每个正整数m,存在唯一的实对称,半正定矩阵B,使A=Bm.
证由于A实对称,半正定,由定理1存在正交矩阵Q,使得
QTAQ=diag(λ1,λ2,…,λr,0,…,0),
其中,λi>0,i=1,2,…,r.对正整数m,令
则A=Bm.
假设实对称,半正定矩阵C满足A=Cm.由定理1存在正交矩阵P1,使得
其中μi>0,i=1,2,…,s.则有

令P=P1P2.则QTAQ=PTAP=(PTCP)m.
不妨设
QTAQ=diag(λ1In1,λ2In2,…,λtInt,0,…,0),
其中λi≠λj对任意的i≠j.则有
记P=(α1,α2,…,αn),Q=(β1,β2,…,βn).则αni-1+1,αni-1+2,…,αni和βni-1+1,βni-1+2,…,βni是A的属于特征值λi的特征子空间的标准正交基,因此存在正交矩阵Ri,使得
(βni-1+1,βni-1+2,…,βni)=(αni-1+1,αni-1+2,…,αni)Ri.
令R=diag(R1,R2,…,Rt,I).则Q=PR.
=C.
唯一性得证.
类似于上面两例,直接运用定理1就能解决问题,通常学生并不缺少这类能力,他们缺乏把定理1与实二次型的基本特征联系起来融为一体的思考,并由此去解决问题的训练.下面的简单考察对理解定理1是关键的,尽管它是直接易知的.
设实二次型f(x1,x2,…,xn)=XTAX对应的矩阵为A,设A的n个特征值为λ1,…,λp, -λp+1,…,-λp+q,0,…,0,其中每个λi都是正数,p和q都是非负整数,则存在实正交矩阵Q=(α1,α2,…,αn),使
QTAQ=diag(λ1,…,λp,-λp+1,…,-λp+q,0,…,0).
则有如下结论:
i)f(x1,x2,…,xn)的正负惯性指数分别是p,q.
ii) 将α1,…,αp生成的子空间记为V+,对任意非零向量ξ∈V+.记ξ=(u1,u2,…,un)T.则
f(u1,u2,…,un)=(u1,u2,…,un)A(u1,u2,…,un)T>0.
将αp+1,…,αp+q生成的子空间记为V-,将αp+q+1,…,αn生成的子空间记为V0.如果ξ∈V-,则ξTAξ<0;如果ξ∈V0,则ξTAξ=0.显然n=V+⊕V-⊕V0.设δ,∈{+,-,0}且δ≠,若X∈Vδ,Y∈V,则XTAY=0.
例4(惯性定理) 任意一个实二次型,经过一适当的非退化线性替换可以变成规范形,并且规范形是唯一的.
证证明参见文献[1,第五章,定理4].我们将从几何的角度来重述其唯一性.设经过可逆线性替换X=PY,得到
设经过可逆线性替换X=QZ,得到

例5实二次型f(x1,x2,…,xn)=XTAX的正惯性指数p等于{X∈n|XTAX>0}所包含子空间的最大维数.实二次型f(x1,x2,…,xn)=XTAX的负惯性指数q等于{X∈n|XTAX<0}所包含子空间的最大维数.
证由定理1,存在实正交矩阵
Q=(α1,…,αp,αp+1,…,αp+q,αp+q+1,…,αn),
使得
QTAQ=diag(λ1,…,λp,-λp+1,…,-λp+q,0,…,0).
其中每个λi都是正数,p和q都是非负整数.则A的正负惯性指数分别是p,q.记α1,…,αp生成的子空间为V+,αp+1,…,αp+q生成的子空间为V-,αp+q+1,…,αn生成的子空间为V0.则n=V+⊕V-⊕V0.
任取0≠α∈V+,则存在ki∈,1≤i≤p使得
因此得到
αTAα=(k1,k2,…,kp,0,…,0)QTAQ(k1,k2,…,kp,0,…,0)T
>0.
同理,如果0≠α∈V-,则αTAα<0;如果0≠α∈V0,则αTAα=0.
设W⊂{X∈n|XTAX>0},且dimW最大,若dimW>p,则W∩(V-⊕V0)≠0.设0,矛盾.所以dimW=p.
例6如果实对称矩阵A的所有顺序主子式都大于0,则A正定.

例7设A=(aij)正定,则


例8(Hadamard不等式) 设A=(aij)n×n是n阶正定矩阵,则
detA≤a11a22…ann,
并且等式成立当且仅当A是对角矩阵.

事实上,Hadamard不等式等价于AM-GM不等式,见文献[5].
例9(Schur定理) 设A=(aij),B=(bij)正定,则Hadamard积H=(aijbij)正定.


更合理的证明,可以利用Kronecker积A⊗B的正定性.

证设X=(x1,x2,…,xn)T,Y=(y1,y2,…,yn)T,A=diag(Is,-It,0),依题意存在矩阵Q使得Y=QX.二次型f(x1,x2,…,xn)=YTAY=XTQTAQX.由例5,知f(x1,x2,…,xn)的正惯性指数p等于{X∈n|XTQTAQX>0}所包含的子空间V+的维数.注意到V+与QV+同构,则{QX∈n|XTQTAQX>0}所包含的子空间维数为p.又{Y∈n|YTAY>0}包含的子空间的维数为s,所以p≤s.
同理可证q≤t.
例11设A是n阶实对称矩阵.则{X∈n|XTAX=0}≤n当且仅当A半正(负)定.此时{X∈n|XTAX=0}={X∈n|AX=0}.
证由定理1,存在正交矩阵Q使得
QTAQ=diag(λ1,…,λp,-λp+1,…,-λp+q,0,…,0).
其中每个λi都是正数,p和q都是非负整数.则存在空间分解n=V+⊕V-⊕V0,且对任意的X∈V+,Y∈V-有XTAY=0.设W={X∈n|XTAX=0}.假设V+≠0,V-≠0.取X+∈V+,使得取X-∈V-,使得则(X++X-)TA(X++X-)=0=(X+-X-)TA(X+-X-).因此X+±X-∈W.如果W是子空间,则X+,X-∈W矛盾.因此如果W是子空间,则有V+=0,或V-=0.即A半正(负)定.
例12设A是可逆的实对称矩阵.则det(A)<0当且仅当负惯性指数为奇数,并且此时存在X,使得XTAX<0.且det(A)>0当且仅当负惯性指数为偶数,如果n为奇数则存在X,使得XTAX>0.

det(A)>0当且仅当负惯性指数为偶数.如果n为奇数,则正惯性指数为奇数.不妨设λ1>0,X=Q(1,0,…,0)T,则XTAX=λ1>0.
4 几类实对称矩阵的特征值
我们知道,证明定理1的决定性步骤是求出A的所有特征值.只要计算出A的特征值,就可以程序化地求出正交矩阵Q,从而得到标准形QTAQ.由于次数≥5的一元高次方程没有统一化的根式求解公式,计算A的特征值需要见机而行,绝不是一蹴而就的事,即使对专家而言也是如此.就高等代数教学而言,学生在求解矩阵特征值方面受到的训练是远远不够的.许宝騄先生是我国卓有成就的数学家,在矩阵论方面的造诣极深.张尧庭在追思许先生生平时[6],写道:
“记得在1962 年关于正态变量二次型的讨论班上,他要我们报告冯·诺依曼关于时间序列循环相关系数精确分布的论文.他说在40年代,他也考虑了这个问题,但是解决不了,因为一个特定矩阵的特征值很难求,而诺依曼却把特征值和特征向量放在一起来求,这样问题反而解决了,所以从这里他学到了新的东西.”
经查,这段文字涉及了实对称矩阵及冯·诺依曼求解其特征值的方法如下,参见文献[8,Section 3].
例13设
则A有n-1个正的特征值,重根按重数计算.
解设λ为A的一个特征值,则线性方程组(λI-A)X=0有非零解.设x0=x1,xn+1=xn,λ=2-2cosα.则线性方程组(λI-A)X=0化为
xi-1+xi+1=2xicosα,i=1,2,…,n,

用冯·诺依曼的方法可以求解下面的问题.

解记Δn(λ)=det(λI-A).则有Δn(λ)-λΔn-1(λ)+Δn-2(λ)=0.并且Δ-1(λ)=0,Δ0(λ)=1,Δ1(λ)=λ,Δ2(λ)=λ2-1.由递推方程x2-λx+1=0,得
因此,


解记Δn(λ)=det(λI-A).则有Δn(λ)-λΔn-1(λ)-Δn-2(λ)=0.并且Δ-1(λ)=0,Δ0(λ)=1,Δ1(λ)=λ,Δ2(λ)=λ2+1.由递推方程x2-λx-1=0,得
因此,


在求解二次型的正、负惯性指数,判别其有定性等问题时,我们常常不用求特征值的方法.下面的解法不同于文献[9].

解设λ为二次型A的一个特征值,则线性方程组(λI-A)X=0有非零解.即线性方程组2λxi-x2n+1-i=0,-xi+2λx2n+1-i=0,i=1,2,…,n有非零解.任取1≤i≤n,有(4λ2-1)xi=0.由此得λ=±1/2是二次型矩阵A的特征值,对应的解为xi=1,x2n+1-i=±xi,xj=0当j≠i,2n+1-i时.所以λ=±1/2是二次型矩阵A的n重特征值.将特征向量正交标准化,记为ξ1,ξ2,…,ξn,ξn+1,…,ξ2n,设Q=(ξ1,ξ2,…,ξ2n).则线性替换X=QY将二次型化为标准形

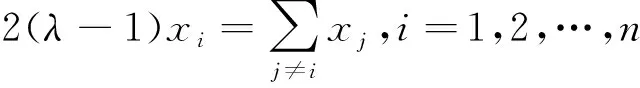

解二次型
设E为n阶各位置全为1的矩阵,则二次型的矩阵为
设λ为二次型A的一个特征值,则线性方程组(λI-A)X=0有非零解.即线性方程组
有非零解.将各个方程相加得到

5 实对称矩阵规范形的应用
任意实二次型f(x1,x2,…,xn)=XTAX可经过可逆线性变换化为标准形.用矩阵的语言可以表述为:
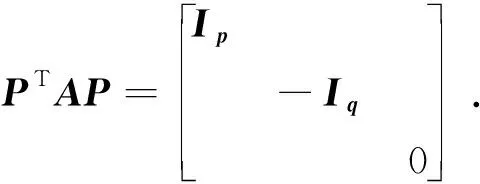
定理3虽然不如定理1精确,但仍是非常有用的,有时比定理1使用起来更方便.
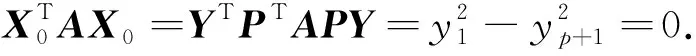
当然例19也可用定理1来证明.事实上,由定理1,存在正交矩阵Q使得
QTAQ=diag(λ1,…,λp,-λp+1,…,-λp+q,0,…,0).
其中每个λi都是正数,由条件知p≥1,q≥1.则存在空间分解n=V+⊕V-⊕V0,取X+∈V+,使得取X-∈V-,使得则X++X-≠0,并且(X++X-)TA(X++X-)=0.
例20设A,B是实对称矩阵.如果A+B正定,则存在可逆矩阵P,使得PTAP,B同时为对角矩阵.

