WOD随机变量序列加权和完全收敛性及其应用
2023-09-07张玉
张玉
(巢湖学院数学与大数据学院, 安徽 合肥 238024)
0 引言
概率论、统计学早期主要成果是关于随机变量的大数定律、中心极限定理,这些理论都要求随机样本是相互独立的,但生活实际中往往随机变量之间内部存在着相互关系这就引入了相依随机变量的概念.相依随机变量序列由于其自身的性质在天文学、地质学、保险、时间序列等等都有广泛的涉及.有学者于20世纪90年代提出负相协NA(negatively association)随机变量序列[1],这是目前最简单的一种相依随机变量序列,WOD随机变量序列由WANG等[2]于2013年提出的,其相关应用也十分广泛,下面给出相关定义:
定义0.1[3]如果对于一有限的实数序列{gU(n),n≥1}满足对∀n≥1,及所有x1,x2,…,xn∈,都有
(1)
则随机变量序列{Xn,n≥1}是宽上象限相依(WUOD)的.

(2)
则随机变量序列{Xn,n≥1}是宽下象限相依(WLOD)的.如果随机变量序列{Xn,n≥1}既是WUOD又是WLOD的,则称随机变量序列为WOD随机变量序列,{gU(n),gL(n),n≥1},称为控制系数.随机变量阵列{Xni,i≥1,n≥1}是WOD的,如果对∀n≥1,{Xni,n≥1}是WOD随机变量序列.当gU(n)=gL(n)=M,对于一些固定的M,随机变量序列{Xn,n≥1}满足(1)、(2)式则分别称为宽负上象限相依(ENUOD)和宽负下象限相依(ENLOD)随机变量序列;如果既是ENUOD又是ENLOD的,那么称随机变量序列为宽负象限相依(ENOD)随机变量序列.当gU(n)=gL(n)=1,随机变量序列{Xn,n≥1}满足式(1)、(2),则分别称为负上象限相依(NUOD)和负下象限相依(NLOD)随机变量序列;如果既是NUOD又是NLOD的,那么称随机变量序列为负象限相依(NOD)随机变量序列.WOD随机变量序列概念提出后很多学者对其进行了研究,SHI WU[3]研究了具有同分布的WOD随机变量序列样本下密度函数核估计的强相合性;WANG等[4]利用Marcinkiewicz-Zygmund和Rosenthal不等式研究了WOD随机变量加权和完全收敛性并且给出应用;刘振等[5]将NA样本最近邻密度估计的相合性推广到WOD随机变量序列;WANG等[6]探讨了WOD随机变量序列下密度函数最近邻估计的一致性;胡学平等[7]利用Rosenthal-型矩不等式和Bernstein-型指数不等式研究了WOD样本下密度函数核估计的收敛性;林君洁等[8]研究了非负WOD 随机变量的第K小矩不等式;ZHANG等[9]研究了WOD随机变量序列加权和收敛性;LU等[10]研究了WOD随机变量序列加权和最大值完全收敛性和矩收敛性;章茜等[11]根据不同的控制系数获得了WOD随机变量序列完全收敛性;谭希丽等[12]获得了WOD随机变量序列加权和几乎处处收敛性;KADDOU等[13]获得了WOD随机变量序列中心不等式和完全收敛性,在前面学者的研究基础上采用新的证明方法获得WOD随机变量序列完全收敛性.
1 预备知识
下面给出完全收敛性的定义以及证明要用到的随机控制的定义.
定义1.1[14]{Xn,n≥1}是定义在概率空间{Ω,F,P}上的随机变量序列,a为任意常数,对∀ε>0,
那么随机变量序列{Xn,n≥1}完全收敛于a.
定义1.2[14]如果随机变量{Xn,n≥1}被称为被一随机变量X随机控制,如果存在一正常数C使得对所有的x≥0和n≥1满足:P(|Xn|>x)≤CP(|X|>x).
随机变量阵列{Xni,i≥1,n≥1}被称为被随机变量X随机控制,如果存在一正常数C使得对所有的x≥0,和n≥1满足:P(|Xni|>x)≤CP(|X|>x).
获得完全收敛性之后,再将完全收敛性应用到WOD随机变量误差的非参数估计中,考虑如下非参数回归模型:
(3)
其中,xni为已知固定来自于集合A点的列,A∈Rn,n≥1为正整数,g(·)为未知的定义在集合A上的回归函数,εni为随机误差,假设对∀n≥1,随机误差εni服从相同的分布,那么g(·)作为一个估计它的加权回归估计为:
(4)
其中,Wni(x)=Wni(x;xn1,xn2,…,xnn),i=1,2,…,n为权函数.
非参数回归模型很多学者做了大量研究,周兴才等[15]研究了负相依NA样本误差下最小二乘估计以及加权最小二乘估计的矩相合性;于德明等[16]研究了混合随机变量序列误差下回归函数加权核估计的一致性;张鸽等[17]研究了渐近几乎负相依AANA(asymptotically almost negatively associated)随机变量序列的回归模型的一致性;唐玲等[18]探讨了φ-混合序列滑动和过程回归模型的相合性;彭智庆等[19]探讨了误差为NOD样本下的非参数回归模型估计的相合性;张水利等[20]探讨了NOD误差下非参数回归函数积分权估计的完全相合性.
为了获得WOD随机变量序列完全收敛性要用到如下引理.
引理1.1[6]如果随机变量X1,X2,…,Xn是WOD随机变量序列,且f1,f2,…,fn全是非降或非增函数,则f1(X1),f2(X2),…,fn(Xn)也是WOD随机变量序列.
引理1.2[6]设{Xn,n≥1}是WOD随机变量序列,那么对任意n≥1和任意常数s∈R,
引理1.3[6]设{Xn,n≥1}是被随机变量X随机控制的随机变量序列,则对任意的α>0和b>0,有下面两式成立:
E|Xn|αI(|Xn|≤b)≤C1[E|X|αI(|X|≤b)]+bαP(|X|>b),
E|Xn|αI(|Xn|>b)≤C2E|X|αI(|X|>b).
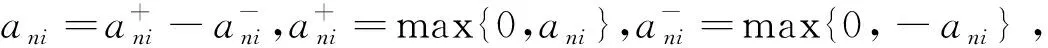
2 主要结果及证明
定理1若{Xni,i≥1,n≥1}是被随机变量X控制的WOD随机变量阵列,EXni=0,g(n)是控制系数,若α>2β,β>0,An≤Kn-α-2,E|X|<∞,那么对∀ε>0,
(5)
定理1的证明
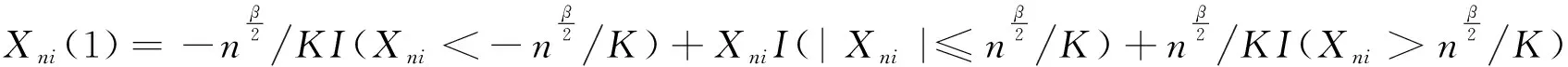
(6)
(7)
(8)
(9)
根据集合间的关系可知:
(10)
记(10)式中的后面为T1+T2+T3,要获得(5)式的结果,现只要证明T1+T2+T3<∞,根据(6)式以及引理1.1、集合间关系,下证T1<∞.
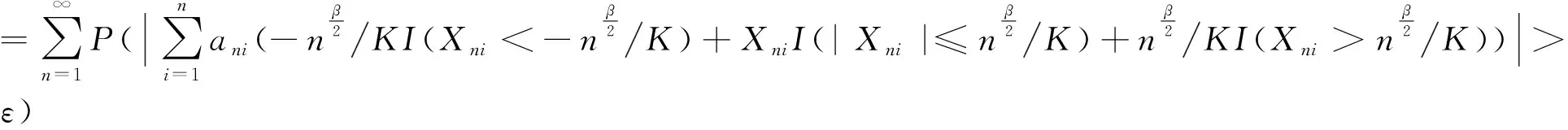
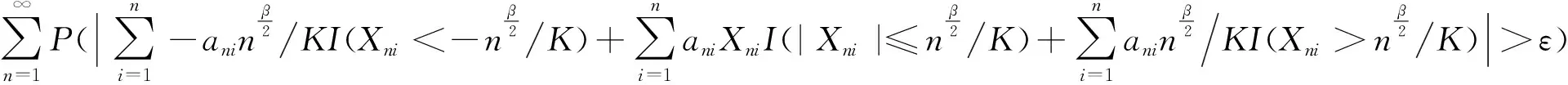
(11)
记(11)式中后面等式为:T11+T12+T13.
因为|ani|≤KAn,An≤Kn-α-2由马尔可夫不等式可知:
(12)
下证T12<∞.
如果随机变量X≤1,那么存在事实:EeX≤eEX+EX2,令0 Eexp{t|aniYni|/An}≤exp{E(t|aniYni|/An)+E(t2ani2Yni2/An2)} ≤exp{t2ani2EYni2/An2} (13) (14) 根据(12)、(13)式所以: (15) 不妨取t=n-2β-2,那么: (16) T11+T12+T13<∞,这就完成了T1<∞的证明. 下证T2<∞. 由(7)式以及集合间关系: (17) 记(17)式后面部分为T21+T22. 由引理1.1~1.3可知: (18) 再由马尔可夫不等式可知: (19) T21+T22<∞,这就完成了T2<∞的证明. 根据(8)式: (20) 证明T3<∞的过程与证明T2<∞的过程类似,在此省去证明. 综上所述可得T1+T2+T3<∞,这就获得了WOD随机变量序列加权和的完全收敛性. 下面将获得的WOD随机变量序列加权和完全收敛性应用到非参数回归模型中,得到如下结论. 那么对任意的x∈C(g)(C(g)为g(x)在集合A上的点列),有 Egn(x)→g(x) (21) 定理2的证明对任意的x∈C(g),a>0,依据(3)、(4)式可得: (22) 由于x∈C(g)对ε>0,存在δ>0,使得当‖x′-x‖<δ时,|g(x′)-g(x)|<ε,取a∈(0,δ),由(22)式可得: 根据条件I)~Ⅲ)可知: (23) 根据(23)式,获得(21)式只要证明: (24) (25) 由定理可知令Xni=εni,ani=Wni即可获得(25)式成立,这就完成了定理的证明. 回归模型在实际应用中十分广泛,以相依随机变量序列为误差的非参数回归是重要的模型之一,涉及多方面的应用领域.依据WOD随机变量序列本身特点,结合随机变量尾截技术以及引理2的创新应用,获得WOD随机变量序列加权和完全收敛性,再将结果应用到非参数回归模型,推广了NA等随机变量序列收敛性的应用,丰富了概率极限理论,以及回归模型的应用.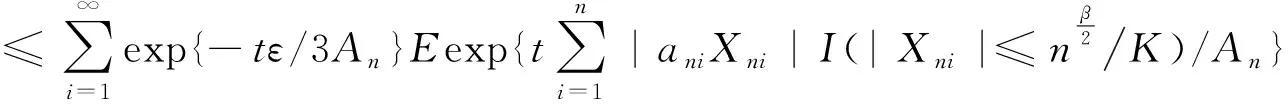

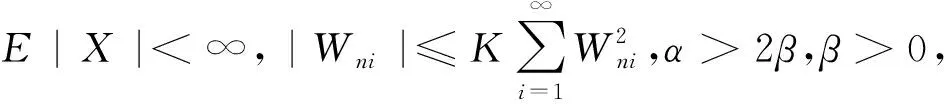
3 结束语
