李鸿飞

摘 要 “多解探究”培养学生思维宽度，能够弥补学生单一的思维方式和解题方法，开拓学生视野，提升学生的解题效率;能促进学生对同一问题从更深层次进行思考，巩固之前所学内容并对其开拓创造。以苏科版八年级几何为例，从不同角度进行图形构建，分析和探讨“一题多解”对于提高学生数学素养的作用。

关键词 中学数学 一题多解 图形构建

在数学教学中，一题多解探究可以培养学生发散思维，多角度看问题，多方位处理问题的能力。通过多解探究的练习能够沟通新旧知识之间的联系，提高学生应用所学基础知识和基本技能解决实际问题的能力，从而加深对所学知识的理解，开拓解题视野，提升解题效率。下面，笔者通过一道八年级几何证明题，通过图形构建的多种证法来说明“一题多解”对学生数学核心素养培养的重要作用。

题目：如图1，△ABC中，∠BAC = 90°，AB = AC，直线CD∥BA。动点P是线段BC上的一点（靠近点C的一点），连接AP，过点P作PE⊥AP交直线CD于E。试探究PA与PE的关系。

分析：本题给出的条件有四个：一是∠BAC = 90°，二是AB = AC，三是CD∥BA，四是PE⊥AP。从本题可以看出，通过已知条件很难找到与所求之间的关系，这时我们就要通过作辅助线来解答[1]。对于同一个问题，不管如何选择辅助线，都要先对已知条件和结论进行分析。要证明PA = PE，有三种解题思路：（1）只要证明这两条线段所在的两个三角形全等，然后利用全等三角形的性质证得PA = PE;（2）可以找出第三条线段，使得PA（或者PE）线段长度都等于这条线段长，最后利用等量代换证得PA = PE;（3）可以把这两条线段放在同一个三角形中，利用等腰三角线的判定定理证得PA = PE。笔者在实际教学中，通过以下几个方面，对此题进行研究，给出如下不同的解法。

一、巧用截取构建图形

分析：对于学生来讲，一般情况下，要证明两条线段相等，只要证明这两条线段所在的两个三角形全等，然后利用全等三角形全等性质，来证得PA = PE。那么如何才能构造两个全等三角形，这就需要教师引导学生从题目的已知条件和结论入手，展开想象、大胆尝试，在对题目条件和图形有一个整体的把握后，截取并构造两个全等三角形。

证法1：如图2，在直线CD上取一点Q，使得PQ = PE，连接PQ。

因为∠BAC = 90，AB∥CD。所以∠BAC = ∠ACD = 90°。因为AP⊥PE，所以∠APE = ∠ACD = 90°。因为∠AFP = ∠CFE，所以∠PAC = ∠PEC。而PQ = PE，所以∠PQE = ∠PEC，所以∠PAC = ∠PQE。又因为∠BAC = 90°，AB = AC，∠ACD = 90°。所以∠ACB = ∠ABC = ∠PCQ = 45°。PC = PC，易证△CPA ≌ △CPQ，所以PA = PQ，因为PQ = PE，所以PA = PF。

除证法1的截取方法外，还有另外两种截取方法。证法2：如图3，延长射线AC，在射线AC上取点Q，使得PQ = PA，连接PQ，易证△PCE ≌ △PCQ，所以PQ = PE，因为PQ = PA，所以PA = PE。证法3：如图4，过点P作PH⊥BC交AC与点H，只需要证△APH ≌ △EPC，所以PA = PE。

以上三种证法都使用了巧妙的截取。什么时候才能想到截取？当题设中无法直接证明所要求的结论时，就要寻找第三变量，利用“转化”的数学思想方法，从而化繁为简、化难为易、化未知为已知。

二、善用对称平行构建图形

分析：从图形和已知条件中，可以看出∠ACB = ∠BCN（图5）可能是对称的，这就可以让学生们联想猜测BC可能是∠ACN的角平分线，然后利用角平分线这个特殊图形及其性质解决问题。

证法4：如图5，过点P作PM⊥AC，PN⊥CD，垂足分别为M，N。

因为∠BAC = 90°，AB∥CD。所以∠BAC = ∠ACD = 90°。因为AP⊥PE，所以∠APE = ∠ACD = 90°。因为∠AFP = ∠CFE，所以∠PAC = ∠PEC。又因为∠BAC = 90°，AB = AC，∠ACD = 90°。所以∠ACB = ∠ABC = ∠BCN = 45°。所以CB是∠ACN的角平分线，因为PM⊥AC，PN⊥CD，所以PM = PN，∠PMA = ∠PNC = 90°。易证△PMA ≌ △PNE，所以PA = PE。

同理，还可以过点B作BQ⊥CD，连接PQ（如图6），证明方法同证法4。

对称性是数学美的最重要特征，几何中的对称轴、中心对称以及在代数中的许多运用都能给人以美感。本题中以直线BC为对称轴，由此想到了正方形这个基本模型和角平分线的性质。以此为突破，从而很快解决了这个问题。所以，时刻要把数学的对称美贯穿在学习中。由对称性联想到利用构造平行线的方法，由此得到证法6和证法7。

證法6：如图7，过点P作AB的平行线交AC于点M，过点E作EN⊥PM，垂足为N。可证出四边形MCEN为矩形，所以NE = MC。易证得△AMP ≌ △PNE，所以PA = PE。

证法7：如图8，过点P作PM∥AC交线段AB和直线CD于点M，N。可证出四边形AMNC为矩形，所以AM = NC。易证得△PAM ≌ △EPN所以PA = PE。

构造平行线探究基本规律，这是数学中常见的思维方法，本题中要证明PA = PE，就要把这两条线段分别放在两个特殊的直角三角形中。

三、利用旋转构建图形

分析：通过类比构造平行线的方法，我们也可以想到构造平行四边形这个特殊的模型来解决这个问题。根据题目中的条件可以巧妙地构造之前学过的平行四边形，基于平行四边形模型，可以将△EPC围绕某个点进行不同的旋转，从而解决这个问题。

证法8：如图9，过点A作AM⊥BC，并延长AM，过点P作PN∥CD交AM的延长线于点N，连接CN。因为AB = AC，∠BAC = 90°，AM⊥BC。所以AM = MC = MB，∠B = ∠ACB = 45°。因为AB∥CD，CD∥NP，所以NP∥AB∥CD，所以∠B = ∠MPN = 45°。因为AM⊥BC，所以∠PMN = 90°，所以∠MPN = ∠MNP = 45°，所以MN = MP，所以△AMP ≌ △CMN，所以PA = NC，∠PAM = ∠MCN。又因为PA⊥PE，AM⊥BC，所以∠PAM+∠APM = ∠APM+∠EPC，所以∠PAM = ∠EPC，因为∠PAM = ∠MCN，所以∠EPC = ∠MCN，所以PE∥NC，因为PN∥CE，所以四边形PNCE为平行四边形，所以PE = NC，而NC = PA，所以PA = PE。

同理，过点C作CN⊥PC，使得CN = PC，过点N作NM∥PA交AC于点M，连接PN，如图10，可得证法9，证法同证法8。

因此，在解决问题时我们要思考解法与解法之间的联系与区别，要能够触类旁通。所以在解决数学问题时，我们往往会想到用类比的数学思想方法。由平行可以巧妙地构造“特殊形”，即学过的平行四边形，通过平行四边形的性质来解决这个问题。

四、构造辅助圆构建图形

分析：借助等腰三角线的性质来解决这个问题，由PE⊥AP会想到直角，由直角会想到构造辅助圆来解决问题，由此可以借助初三圆的知识点来解决这个问题相对比较简单。

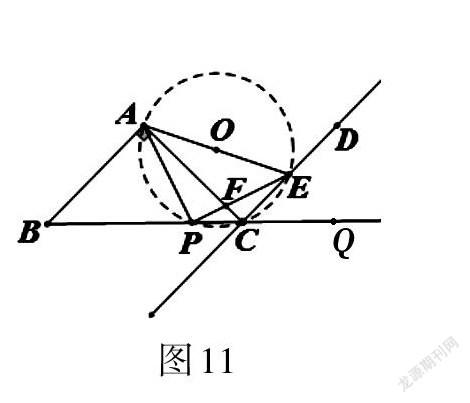
证法10：如图11，在BC延长线上取点Q，连接AE。取AE的中点O，以O为圆心，OA为半径画圆。因为∠BAC = 90°，AB = AC，所以∠ACB = ∠ABC = 45°。所以∠AEP = ∠ACB = 45°。因为∠BAC = 90°，AB∥CD。所以∠BAC = ∠ACD = 90°。所以∠ECQ = ∠ACB = 45°。因为四边形APCE内接于圆内，所以∠ECQ = ∠PAE = 45°。即∠PAE = ∠AEP = 45°，所以PA = PE。

怎么会想到用构造辅助圆来解决问题的呢？这就要求学生对圆的知识要足够的了解，特别是怎样才能确定圆。（1）不在同一条直线上的三点可以确定一个圆;（2）直角三角形也能确定一个圆;（3）当一个图形的一个角和角所对的边确定时，也能确定圆（即定角定弦隐圆）。那么，本题应是定角定弦隐圆的情况。

五、总结与反思

数学是思维的体现，怎样才能培养学生的数学思维能力，这是数学教学过程中所要认真思考的问题。通过“一题多解”，“多解归一”的学习能培养学生思维的灵活性[2]，能够激发学生的创造力，可以加深学生对所学知识的理解，训练学生数学方法的运用，可以使学生对之前所涉及的知识进行分析、归纳、总结，从而提高运用知识的能力和解题的能力，解题的视野得到开拓、解题的效率得到提升，从而提升学生的数学综合能力。为培养学生“一题多解”的能力，要注意以下几个问题：

1.引导学生建立基本的模型，培养解题能力。教师在平时教学时引导学生总结出一些常见的几何基本模型，并能够运用基本模型解题。平时注重基本模型的积累，积累的越多，越有助于激发学生提高解题的能力，有助于培养学生的创新意识。

2.引导学生注重解法類比，提高解题效率。在数学解题过程中，类比推理的方法可以解决很多类似问题，能够找到同类问题的思路，让问题更加清晰，让复杂的问题简单化，让隐含性的问题更加显性化。在初中教学中大胆使用类比方法，能够提高学生的解题效率。

[参 考 文 献]

[1]陈红伟.一题多解练思维多解归一探本质[J].中学数学教学参考，2019（30）：31-32.

[2]金敏，王红兵.立足核心素养彰显思维品质[J].中学数学教学参考，2019（32）：30-32.

（责任编辑：杨红波）