余立海　栗小妮

【摘 要】研究者利用14世纪意大利的一个关于土地分配的法律案例设计圆的基本性质复习教学，引导学生利用角平分线的性质、三角形的两边之和大于第三边、同一直角三角形中斜边大于直角边等知识对原法律案例进行解释，通过对原法律案例进行问题变式，让学生综合运用与圆的基本性质有关的知识解决问题，提升了数学建模的意识与能力，并整体性复习初中阶段与圆相关的知识。

【关键词】圆的基本性质;数学史;数学建模

【作者简介】余立海，杭州市萧山区南阳初级中学数学教师;栗小妮，教育学博士，上海市长宁区教育学院教研员。

【基金项目】上海高校“立德树人”人文社会科学重点研究基地之数学教育教学研究基地研究项目——数学课程与教学中落实立德树人根本任务的研究（A8）

在全国积极深化义务教育课程改革，落实立德树人根本任务之际，研究适合改革需要的课堂教学刻不容缓。然而，笔者经调查发现，当前已有的复习课教学大部分以“练习+讲评”为主[1]，课堂教学乏味且低效。很多教师对课程标准、教材以及试题缺乏研究，直接将教辅资料的内容作为上课的主要内容。还有的教师因为复习课时间紧，往往采用一讲到底或边做边讲的模式，学生没有思考和表达的机会。复习课的教学目的之一是将碎片化的知识体系化，而有的教师因为找不到合适的线索把要复习的知识串联起来，所以只能让学生重复操练，学生往往不清楚自己解决了什么问题。究其原因，主要是教师未能提供相对真实并可供解决的问题背景。

整体教学以知识的相互关联性、整体性与学习者的参与性为原则[2]，倡导情境式的、问题定向的、案例式的、社会性的和内在驱动的教学方式，利用讲练结合、支架式生成与建模等策略使学生获得有意义的学习[3]。而复习课就是要帮助学生建构知识之间的联系，形成对知识的整体理解，在建立知识之间的联系的过程中，领悟数学的思想方法，在应用知识解决问题的过程中，积累数学活动经验[4]。所以，笔者尝试利用中世纪一个典型的法律案例进行单元整体复习教学设计，让学生参与到有意义的情境任务中，通过问题解决，建构和完善相关知识体系。

一、历史素材

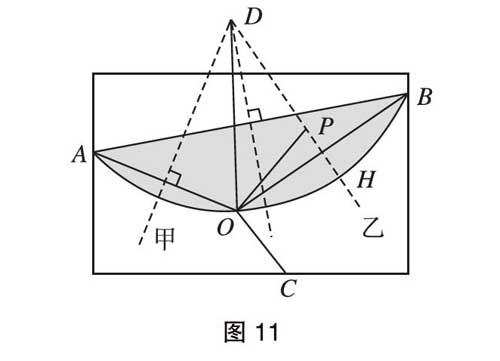
1355年，意大利法律教授巴托鲁斯（Bartolus）讨论过一个关于淤积地分割的案例：如图1，具有公共边界OC的甲、乙两块土地的主人都想获得洪水过后所产生的一块肥沃的淤积地OAB（其中甲、乙两块土地与淤积地接壤的边界为不规则曲线AOB，河岸线AB也为不规则曲线），双方该如何分割淤积地呢？

有人建议延长已有的分割线CO将淤积地进行分割，但这样的分割方式可能会引发争端。巴托鲁斯教授意识到要公正合理地解决这样的问题非常重要。他发现早在公元160年的罗马法律著作中就有类似的问题出现，法律著作中虽然没有给出实际的解决方案，但给出了一个一般性的分割原则。淤积地是由于河水沖刷原有的土地而形成的，那么分割的原则就是“冲刷谁的地形成的归谁”。基于这样的原则，巴托鲁斯教授给出了淤积地分割的方案：淤积地中的任何区域，离谁家原有土地更近，就归属谁家。

巴托鲁斯教授将这一原则应用于不同的几何情境中。如若边界线AOB是一条线段，那么，分割线就是过点O作垂直于AB的线段;若边界线AOB构成一个角（如图2），那么，分割线就是∠AOB的角平分线;若边界线AOB构成圆弧，则分割线是圆心与点O的连线。

荷兰学者冯马楠（Jvan Maanen）认为，将类似这样的生活中的真实问题融入课堂，可以实现数学和其他学科的融合，如本案例可以实现数学和法律的融合，让学生用数学的方法解决法律问题，体会数学的应用价值。这样的分割原则，在一些国家的法律中现在也依然在用[5]。

“圆的基本性质”是浙教版数学九年级上册第3章的教学内容。学习圆的基本性质对于学生逻辑推理能力的培养，数学思想方法的形成都有着重要的价值。基于以上原因，笔者利用上述法律案例设计问题串，对圆的基本性质复习课进行教学设计，并拟订以下教学目标。

（1）能对本法律问题发表自己的观点，知道问题的历史解决方案，并知道法律问题的解决需要满足公平、公正和可操作的原则。

（2）能通过建立数学模型，根据圆的基本性质和相关知识解决该问题的延伸问题串，培养学生分析问题和解决问题的能力。

（3）在问题解决过程中，体会数学的应用价值。

二、教学设计与实施

（一）情境引入

教师将原法律案例进行了改编（将分割线OA、OB分别改成了线段[6]），如图2，并在上课前一天发放学习单，让学生自行设计分割方案。

课上，教师投影部分学生的分配方案，然后让对应的学生说明自己设计的分配方案的依据，教师在学生表达自己的观点后与其他学生一起进行评价。

师：根据收集上来的统计情况，同学们的分配方案主要有平均分配、补差分配、按比例分配、按分割线分配等，其中大部分同学都是按分割线分配，可见大家都喜欢从数学的角度来思考问题。老师选了一些比较典型的分割线分配方案，请同学们自己来说一说这样分配的依据。

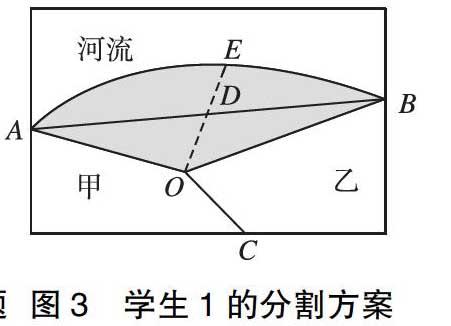
生1：我想尽量平均分配，方法是连接AB，取AB中点D，连接OD并延长至河岸线交于点E，OE为分割线（如图3）。

师：这位同学表述非常规范，用了“尽量”平均，因为他这样操作并不一定能平均。

生2：我也是想尽量平分面积，方法是取河岸线AB的中点C，连接OC即为分割线。

师：这位同学也用了“尽量”平分，因为他这样操作也并不一定能平分，而且不规则曲线AB的中点很难找到。

生3：我是想尽量按比例分，方法是过点O作一条分割线使得Sa∶Sb=S甲∶S乙。

师：由于不规则，这位同学的分割线也很难准确得到。

生4：我是想尽量平分面积，方法是连接AB，作AB的中垂线，中垂线与河岸和边界的交点连线作为分割线（如图4）。

师：这位同学也想平分这块淤积地的面积，但这样的操作也无法真正平均分配。

师：听了同学们的讲解，我发现大多数同学都希望平均分配，都希望公平、公正地解决这个问题，但具体的操作和同学们所想的依据并不完全符合，而按比例分配可能会造成多的越多，少的越少的情况，也无法得到甲、乙双方的认可，而且操作起来也非常困难，那么当初这个问题又是如何解决的呢？我们一起来看一下。

教师先出示巴托鲁斯教授的分配依据——就近，并说明此依据当初得到了甲、乙双方的一致认可，然后介绍在这样的依据下的具体操作，并提出新的问题。

师：巴托鲁斯教授这样操作为什么符合离谁原有土地边界近就归谁这个依据呢？

生：他利用角平分线的性质，角平分线上的点到角两边的距离相等。

师：那为什么角平分线右边的点离乙的边界OB更近呢？

生：假设任意取点P，先向两个边界作垂线段，记作PM、PN，量取后进行比较即可。

师：你说的方法能解决点P，但其余的点呢？我们都靠量取的话这个工作能做得完吗？

生：如图5，我们可以记PM与角平分线的交点为C，过点C再作OB的垂线，与OB交于点M′，由角平分线的性质可得CM=CM′，所以根据三角形两边之和大于第三边，以及在同一三角形中，斜边大于直角边可以得到PM=PC+CM=PC+CM′>PM′>PN。

师：同学们借助数学知识科学地解释了点P离分界线OB比较近，由于点P的任意性我们可以说明角平分线右侧的点都离分界线OB比较近，反之也可以用同样的方法去说明左侧的点离分界线OA比较近，这样就能解释他的操作是符合当时的分配依据的。

（二）情境再创

因为本节课的目标是复习圆的基本性质，而且学生之前的分割方案中已涉及圆的相关性质，所以教师采用对学生分割方案通过情境再创的方式进行问题设计，这样既可以缩短理解新问题的时间，又可以提高学生的学习兴趣。

问题1：如图6，在学生做法的基础上，连接AB，分别作AB与OB的垂直平分线，并交于点D，若此时淤积地的法定分割线恰为OD的一部分，判断原边界线OA和OB的数量关系。

生1：如图6，过点D作AO的垂线交AO于点M，因为DN⊥BO，且DO是角平分线，则由角平分线的性质定理可得到DM=DN，作图可知点D是△ABO的外接圆圆心，所以根据圆心角定理的逆定理可以直接得出AO=BO。

生2：由DO是角平分线，则∠AOD=∠BOD，又因为点D是△ABO的外接圆圆心，所以根据圆周角定理的推论——同圆或等圆中，相等的圆周角所对的弧相等，可以得到与弧AO和弧BO度数互补的弧相等，则AO=BO，再根据圆心角定理逆定理可以得到AO=BO。

生3：还可以先证明△DOM≌△DON，得到MO=NO，然后由垂径定理得到AO=2MO，又由条件知BO=2NO，得到AO=BO。

师：很好，同学们用到了圆周角定理的推论、圆心角定理逆定理、垂径定理以及三角形全等等数学知识证明AO=BO。

（三）问题迁移

在不改变分割规则的前提下，教师通过改编原始图形设计问题，让学生在解决问题的过程中，进一步复习圆的相关性质。

问题2：如图7，边界线AOB为长度80米的线段，且河岸线为一段半径为50米的圆弧，则淤积地的法定分割线如何画？[6]

图7

生：只要过点O作AB的垂线交弧AB于点H，OH即为所求分割线，其实还是角平分线，只是现在是一个平角而已。

师：非常好，这位同学不仅给出了分割线，还解释了原因。那这个法定分割线OH的长度可求吗？

生1：会随着O点位置的改变而改变，只有点O确定才可求。

师：那我们选一个特殊的位置，比如中点，然后试着计算它的长度。

生2：如图8，延长HO，由HO是弦AB的中垂线，根据找圆心的方法可知圆弧AB所在圆的圆心一定在射线HO上，假设为点D，连接BD，由勾股定理可得DO=30米，则HO=20米。

师：那如果不是中点，而是AO∶BO=1∶3，还可以求吗？

生3：如图9，在原来的基础上假设有一点O′满足AO′∶BO′=1∶3，再构造一个由半径、半弦、弦心距组成的Rt△DMH′，和刚才一样利用勾股定理就可以求解。

师：非常好，从方法上来看，在知道半径和弦长的情况下，只要知道AO∶BO的值，就可以求出此时分割线OH的长度，请同学们课后思考AO∶BO=1∶n时的情况。

（四）变式深化

在不改变分割规则的前提下，教师在问题2的基础上，进一步改编原始图形，将边界线改为圆弧，让学生寻找解决问题的方案。

问题3：如图10，若边界线AOB为圆弧，该如何分配淤积地？[6]

師：如果我们继续改变边界线和河岸线的形状，若边界线AOB为圆弧，则按照刚才的分配依据，你能不能把分割线画出来？

生1：如图11，在淤积地区域任意找个点P，那么从图中点P的位置可以猜想点P与边界AO的最近的点就是点O，即PO的长，而点P与边界BO最近的点是过圆心D时直线DP与边界BO的交点H，即PH的长，目测PH

师：谁能借助已学的数学知识用推理的方式解释PH

生2：根据三角形中任意两边之和大于第三边得PD+PO>OD=DH=PD+PH，即PH

师：也就是说，淤积地中任意一个点与圆心D连接的直线与边界线的交点在哪家边界上就离哪家的边界近，这样就能解释为什么分割线是DO上的一段。

（五）回顾总结

在该教学环节，教师引导学生从以下几个方面进行总结。

（1）一个原则。淤积地分割问题的解决原则是对双方都公平、公正，即双方都认可的分配方案且具有可操作性。从最初的淤积地分割到教师改编的问题2、问题3都遵循了一个基本准则——就近。

（2）一块知识。本节课利用淤积地分割问题整体复习了与圆的性质有关的知识。在分配方案的解决过程中，主要运用以下数学知识：①角平分线上的点到角两边的距离相等;②三角形的两边之和大于第三边;③直角三角形的斜边大于直角边。在问题1的解决过程中，主要复习的数学知识有：①不在同一直线上的三点确定一个圆;②圆心角逆定理——在同圆或等圆中，相等的弦心距所对的弦相等;③圆周角定理的推论——同圆或等圆中，相等的圆周角所对的弧相等;④圆心角逆定理——在同圆或等圆中，相等的弧所对的弦相等;⑤全等三角形的判定方法（AAS）;⑥垂径定理——垂直于弦的直径平分弦，并且平分弦所对的两条弧。

问题2和问题3都对原情境进行了改编，增加了学生的思维难度，考查学生综合利用知识的能力。问题2主要运用的数学知识包括垂径定理推论，即垂直于弦（弦非直径）并平分弦的直线过圆心，以及与圆有关的计算;问题3在新的情境下寻找分配方案，本质上是圆内一点到圆周的最短路径问题，学生需通过仔细审题，将现实问题抽象为数学问题后再寻求解决方法。

（3）一种思想。基于历史上的法律问题设计问题串，用数学知识来分析和解决现实问题。在不同的情境下，用数学方法来解释“就近”原则，体现了数学的模型思想和应用价值，让学生学会用数学的眼光看待世界，用数学知识解决现实问题，用数学语言描述现实世界。

三、学生反馈

课后，笔者收集了该班25名学生对于本节课的反馈信息。对于“通过这节课，你体会到了学习数学有哪些价值？”这个问题，有18名学生提到了可以利用数学知识解决生活中的实际问题;有6名学生提到了学习数学可以帮助思维更有逻辑性;有1名学生提到了可以用类似的方法解决其他的问题。由此可以看出，数学史融入数学课堂能使学生更深刻地体会到数学的广泛应用性和严谨性。

对于“你认为要解决本节课所遇到的法律问题应遵循怎样的原则？”这个问题，96的学生提出应遵循公平、公正、可操作的分配原则，由此可以说明，数学史融入课堂教学对学生学习是有意义的。

对于“这节课你印象最深的是什么？为什么？”这个问题，有8名学生提到了用数学知识解决法律问题，认为学习数学知识有实际应用价值;7名学生提到了一题多解，认为问题1的解法多种多样，很有意思，也让他们知道解题思路的多样性;7名学生提到了主要用到了圆的基本性质解决问题，复习了圆的基本性质;3名学生提到了各种分配方案。

四、教学反思

本节课利用淤积地分割问题设计问题串，一方面让学生在解决问题的过程中整体性复习与圆的性质有关的知识，另一方面，通过问题的不断改编和层层深入研究，让学生在不同情境下基于“就近”原则，给出了不同数学解释，让学生体会数学的应用价值。

本节课对淤积地分割问题的研究主要可以分为三个阶段。第一阶段，无原则尝试分割。课前教师利用学生学习单展示问题，让学生设计分配方案。课上展示方案，激发学生的学习兴趣，让学生有机会表达自己的观点，大部分学生的分配分案都是基于自己对问题的理解并用数学知识进行了初步的分割操作，但分割存在无原则或者不好操作的问题。第二阶段，初步尝试按“就近”原则分割。教师展示了历史上巴托鲁斯教授给出的分割原则，并让学生利用所学知识进行分割，并给出解释，学生初步用数学的方法解释“就近”原则，通过教师的设问，初步复习了与圆的性质有关的知识。第三阶段，不同情境下的“就近”解读。问题2和问题3是将淤积地的形状改变后，让学生重新用数学的方法解读已有的分割原则，体会不同情境下“就近”的不同数学解释，进一步用数学的语言描述现实问题。在将现实问题抽象为数学问题解决的过程中，利用与圆的性质有关的知识解决问题。

不同情境下的分割方案均隐藏着统一的“就近”原则，让学生体会到解决法律问题时对于公平、公正要求的数学解释。在利用数学知识解决问题时，让学生感受到严谨的数学精神，感受到做人做事要讲“道理”，彰显了德育之效。

参考文献：

[1]陈建国.开发教材为素材，演绎复习更精彩：浙教版数学九上《圆的基本性质》复习课教学设计[J].数学教学，2019（6）：6-13.

[2]王海青.論整体主义教学[J].全球教育展望，2019（4）：34-44.

[3]冯锐，刘丽丽.整体论视阈下的教学设计探讨[J].开放教育研究，2009（4）：69-73.

[4]丁福珍.整体观指导下的初中函数单元总复习实践研究[J].数学通报，2020（4）：47-51.

[5]VAN MAANEN J.Teaching geometry to 11 year old “medieval lawyers”[J].The Mathematical Gazette，1992（475）：37-45.

[6]汪晓勤.一个中世纪法律问题的解决方案和数学教育价值[J].中学数学月刊，2020（1）：42-44.

（责任编辑：陆顺演）