☉江苏省苏州工业园区娄葑学校 彭聪聪

引例是否存在平方和等于1600的两个自然数？

设满足条件的两个自然数分别为x，y，则x2+y2=1600.

或许你会想到从简单自然数的平方和入手：12+22=5，22+32=13，32+42=25等.可1600这个数字有点大了，想把它拆成两个自然数的平方和并不是一件容易的事.能否把1600变小些？比如变成5或13或25等这些比较小的数，

变换称为二元代换.若将x=u+v，y=u-v代入x2+y2=1600，得（u+v）2+（u-v）2=1600.整理得u2+v2=800.

我们发现，虽然仍是平方和形式，但常数减小了一半，这可是个可喜的兆头！我们不妨如法炮制下去.

上面在求x2+y2=1600的自然数解的过程中，通过二元代换这个数学手段，不断地将原方程的常数项减半，使原方程变得越来越简单，变得一眼就可以看出它的自然数解，这实际是一种退步思考问题的方法.

遇到一道较难的数学问题，我们应该怎么办？我国著名数学家华罗庚告诫我们：一个好的办法是“退”，从一般退到特殊，从复杂退到简单，退到你会做、能下手的问题上.我们把这种思考数学问题的方法叫做“退步思考”法.华罗庚的“帽子问题”是就是一道利用“退步思考法”解决数学问题的典范.正如我们在跳远的时候，为了跳得更远，我们在跳远时总要从沙坑边后退一段，然后再起跳.表面上看往后退离目标更远了，这样做正是为了跳得更远，是“以退为进”.下面我们通过实例说明“退步思考”法在数学解题中的应用.

一、从图形一般位置退到特殊位置

许多几何问题给出的图形都具有一般性，蕴含在其中的数量关系和位置关系并不明显.我们不妨先退一步，用一些几何变换手段，使某些基本图形到达某一特殊位置，以便寻求其中的数量关系和位置关系，并由此获得启发，进而找到解决问题的思路和方法.

例1 如图1，△ABC与△DEF均为等边三角形，O为BC、EF的中点，则AD∶BE的值为（ ）.

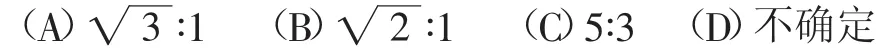
本题的常规解法是从“O为BC、EF的中点”这个条件入手.连接AO、DO，如图2所示.

图1

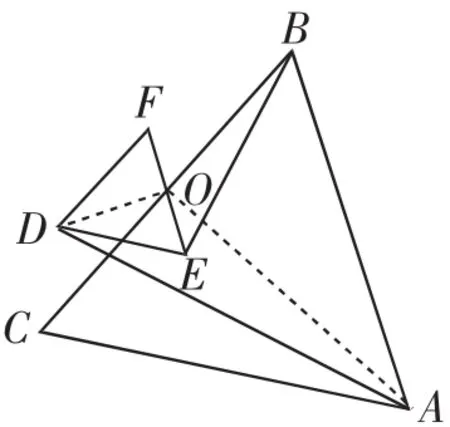
图2

因为△ABC与△DEF均为等边三角形，O为BC、EF的中点，

这种解法显然比较麻烦.不妨取BC⊥EF的情形.

因为△DEF为等边三角形，O为EF的中点，

所以DO⊥EF.

所以点D必然在BC上.再取点D与C重合，如图3.

在Rt△BOE中，∠BOE=

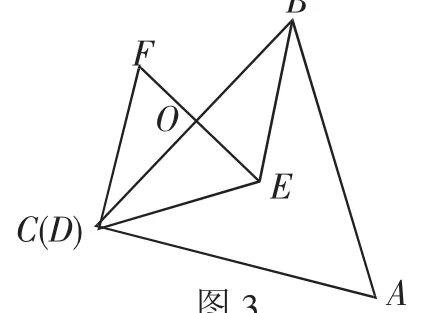
图3

设OE=1，则BE=2，BO=，所以AD=BC=.所以AD∶BE=

这样求解显然简捷，这得益于我们将一般图形变为特殊图形，以便利用特殊的边、角关系求解，同时也便于我们找到本题的一般解题思路和方法，体现了以退为进的解题策略.

二、从抽象字母退到具体数字

我们经常会遇到一类“用代数式描述图形规律”问题.此类问题的本质是求出以图形序号为自变量的函数解析式问题.解决此类问题如果仅仅通过观察很难求出函数解析式，不妨先退一步，从特殊情况（n=1，2，3等）入手，从部分图形中求出某一量的个数，分析其中蕴含的规律，然后归纳出函数解析式.

例2将一些半径相同的小圆按如图4所示的规律摆放，请仔细观察，第n个图形有____________个小圆（用含n的代数式表示）.

直接求解比较困难，不妨选退一步，即先求出n=1，2，3，…时小圆的个数.观察图形不难写出n=1时，小圆个数S1=6；n=2时，小圆个数S2=10；n=3时，小圆个数S3=16……再观察图形我们发现，每个图形中的小圆由两部分组成：最外面的4个小圆和里面的小圆，为了发现规律，可以将小圆个数写成：S1=2+4=1×2+4；S2=6+4=2×3+4；S3=12+4=3×4+4……的形式，其中的规律已经非常明显，从而第n个图形小圆个数为Sn=n（n+1）=n2+n+4.需要说明的是，在探求小圆个数规律时，如果直接根据每个图形中小圆的个数发掘规律比较困难，借助每个图形中小圆的组成规律，再发现小圆的个数规律就变得容易多了.

图4

三、从较强条件退到较弱条件

尺规作图是我们学习几何知识必须掌握的一项基本技能.在进行尺规作图时，往往会给出一些限制条件.比较复杂的尺规作图问题，限制条件还比较多.这时我们不容易一下子作出满足全部限制条件的图形，可以选退一步，放弃某些限制条件，先作出条件符合部分限制条件的图形，然后在已作的图形中利用放弃的某些限制条件继续作图，最后再作出条件全部限制条件的图形.

例3用已知△ABC（如图5），求作△ABC的内接短形DEMN，使DE在BC边上，点M、N分别在AC、AB边上，且DE=2ME.

该题要求作的矩形满足的条件比较多：①DE在BC边上；②点M在AC边上；③点N在AB边上；④DE=2ME.若要同时作出满足这么多条件的图形确实非常困难.我们不妨先退一步，先放弃一个限制条件，假如放弃“点M在AC边上”这个条件，这个矩形就比较好作了，然后再进行位似变换，把点M固定在AC上即可（图形作法略）.

以上我们从三个方面谈了“退步思考法”在数学解题中的应用.当然应用“退步思考法”解决数学问题包括的远不止这些.我们还可以从整体退到局部，从未知退到已知，从复杂退到简单，从不熟悉的情况退到熟悉的情况等等.退的目的是为了更好地前进，更有利于我们找到解决问题的途径和方法，更有利于我们解决问题.只要我们认真总结，勤于思考，用心感悟，一定会将这种思考问题的方法变成我们解决数学问题的有力武器.H

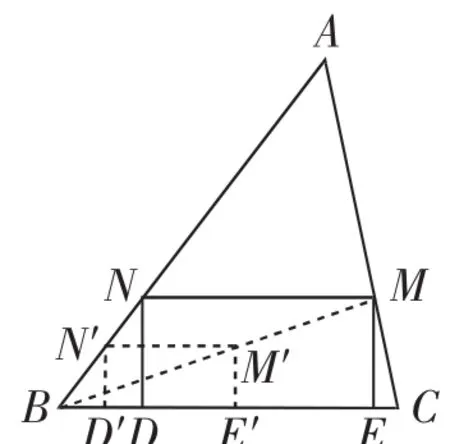
图5