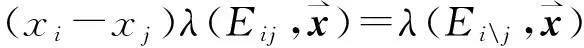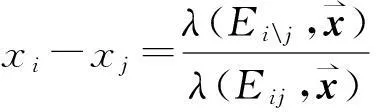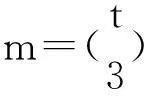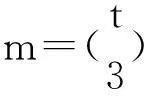An Extremal Problem on Lagrangians of Hypergraphs

YAOYu-ping1*

(College of Mathematics and Econometrics, Hunan University, Changsha 410082, China)

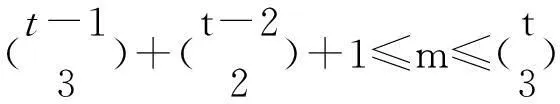
KeywordsLagrangians;FranklandFürediconjecture;colexorder

ForasetVandapositiveintegerr,letV(r)denotethefamilyofallr-subsetsofV.Anr-uniformgraphorr-graphGconsistsofasetV(G)ofverticesandasetE(G)⊆V(G)(r)ofedges.Anedgee={a1,a2,…,ar}willbesimplydenotedbya1a2…ar.Anr-graphHisasubgraphofanr-graphG,denotedbyH⊆GifV(H)⊆V(G)andE(H)⊆E(G).Thecomplementofanr-graphGisdenotedbyGc.Acompleter-graphontverticesisalsocalledacliqueofordert.LetNbethesetofallpositiveintegers.Foranyintegern∈N, we denote the set {1, 2, 3, …,n} by [n]. Let [n](r)represent the completer-uniform graph on the vertex set [n].

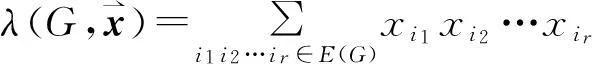
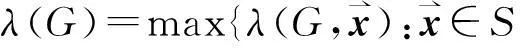
In [1], Motzkin and Straus provided the following simple expression for the Lagrangian of a 2-graph.

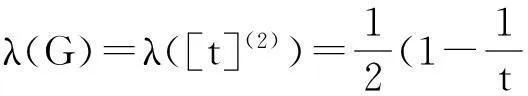
TheobviousgeneralizationofMotzkinandStraus’resulttohypergraphsisfalsebecausetherearemanyexamplesofhypergraphsthatdonotachievetheirLagrangianonanypropersubhypergraph.Indeed,estimatingtheLagrangianofahypergraphismuchdifficult.Lagrangiansofhypergraphshasbeenprovedtobeausefultoolinhypergraphextremalproblems.Inmostapplications,anupperboundoftheLagrangiansofcertainclassofhypergraphsisneeded.FranklandFüredi[2]askedthefollowingquestion.Givenr≥3andm∈N, how large can the Lagrangian of anr-graph withmedges be? For distinctA,B∈N(r)wesaythatAislessthanBinthecolexorderifmax(AΔB)∈B,whereAΔB=(AB)∪(BA).LetCr,mbether-uniformhypergraphwithmedgesformedbytakingthefirstmsetsinthecolexorderofN(r). The following conjecture of Frankl and Füredi (if it is true) provides a solution to the question mentioned at the beginning.

Conjecture 1 (Frankl and Füredi[2]) IfGis ar-graph withmedges, thenλ(G)≤λ(Cr,m).

Definition2Anr-graphG=([n],E)isleft-compressedifj1j2…jr∈Eimpliesi1i2…ir∈Eprovidedip≤jpforeveryp,1≤p≤r.

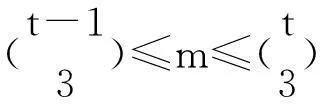
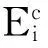
Wearegoingtoprovethefollowingresult.

Theremainingproofofthispaperisorganizedasfollows.InSection1,wegivesomepremilinaryresults.InSection2,wegivetheproofofTheorem2.

1Preliminaries

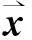
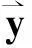
(1)

Remark1Anr-graphG=([n],E)isleft-compressedifandonlyifEji=forany1≤i

ThefollowinglemmagivessomenecessaryconditionsofanoptimalweightingforG.

(a) In Lemma 1, part (Ⅰ) implies that

In particular, ifGis left-compressed, then

for anyi,jsatisfying 1≤i

(b) IfGis left-compressed, then for anyi,jsatisfying 1≤i

(2)

holds. IfGis left-compressed andEij=fori,jsatisfying 1≤i

x1≥x2≥…≥xn≥0.

(3)

We will also give some useful results to apply the following results in the proof.

Sunetal.in[7]provedthatλ(G)≤λ(C3,m)if|EΔE″|≤8.Later,Sunetalextendedtheresults,whichisTheorem3.

2ProofofTheorem2

ProofofTheorem2LetGbethe3-graphsatisfyingconditionsofTheorem5.If[t-1](3)⊆G,thenbyTheorem4,wehaveλ(G)≤λ(C3,m).Otherwise,wewillprovethefollowinglemmaswhichimplyTheorem2.

Next,wewillgivetheproofofLemma4-7.Infact,theproofsofotherthreelemmasaresimilartotheproofofLemma4.Weomitthedetailsoftheproofofotherlemmasandwillgiveonlyanoutlineoftheproofs.InSection2.1,wegivetheproofofLemma4.InSection2.2-2.4,wegivetheoutlineoftheproofofLemma4-7,respectively.

2.1ProofofLemma4

xt+xt-1+xt-2+…+xt-2-i+1-x1≥0.

(4)

To verify (4), we have

(5)

Let us continue our proof. We divide the proof into two cases:a=0 anda≥1.

By Remark 2,

(6)

So

(7)

(8)

(9)

Then

(10)

(11)

(13)

Note that

(14)

where

(15)

and

(16)

(17)

(18)

(19)

(20)

By (4) (14), (18) and (20), we have

(21)

Therefore,λ(C3,m)≥λ(G′)≥λ(G).

2.2OutlineoftheproofofLemma5

We divide the prove into two parts:p=3 andp>3.

PartⅠp=3,thenwehavej+1≥i.Wedividetheproveintotwocases: j≥2andj=1.

2.3OutlineoftheProofofLemma6

PartⅠp=3.Wedividethisproveintotwocases: i=1andi≥2.

PartⅡp≥4.Wedivideourproofintotwocases: p=4, a=0andp≥5ora≥1.

Case1p=4, a=0.Ifj=1,thenwehavei=1ori=2.Wedividethisproveintothreesubcases: j≥2; j=1, i=1; j=1, i=2.

2.4OutlineofproofLemma7

References：

[1]MOTZKINTS,STRAUSEG.MaximaforgraphsandanewproofofatheoremofTurán[J].CanadJMath, 1965,17(1):533-540.

[2]FRANKLP,FÜREDIZ.Extremalproblemswhosesolutionsaretheblow-upsofthesmallWitt-designs[J].JCombinTheorSerA, 1989,52(5):129-147.

[3]TALBOTJ.Lagrangiansofhypergraphs[J].CombinProbabComput, 2002,11(2):199-216.

[4]PENGY,ZHAOC.AMotzkin-Straustyperesultfor3-uniformhypergraphs[J].JGraphsComb, 2013,29(3):681-694.

[5]FRANKLP,RÖDLV.Hypergraphsdonotjump[J].Combinatory, 1989,4(2-3):149-159.

[6]TANGQS,PENGY,ZHANGXD, et al.Someresultsonlagrangiansofhypergraphs[J].DiscAppMath, 2013,166(3):222-238.

[7]SUNYP,TANGQS,ZHAOC, et al.Onthelargestgraph-lagrangianof3-graphswithfixednumberofedges[J].JOptimizTheorAppl, 2013,163(1):57-79.

(编辑HWJ)

极值问题——超图的拉格朗日

姚宇萍*，彭岳建

(湖南大学数学与计量经济学院，湖南 长沙410082)

摘要设G=([t],E)是一个有m条边的左压的3-一致超图，其中，并设[t-2](3)⊆G.本文证明，如果按同余字典序排列中最小元素是(t-p-i)(t-p)并且,则有λ(G)≤λ(C3,m).

关键词拉格朗日；Frankl and Füredi 猜想；同余字典序

中图分类号O157.5

文献标识码A

文章编号1000-2537(2015)06-0068-08

*通讯作者,E-mail：yupingyao1989@163.com, PENG Yue-jian2

基金项目：National Natural Science Foundation of China (No.11271116)

收稿日期：2015-01-27

DOI:10.7612/j.issn.1000-2537.2016.01.012