高雅，张海

(西北大学数学学院，陕西 西安　710127)

具有Log型惩罚函数的稀疏正则化

高雅，张海

(西北大学数学学院，陕西 西安710127)

研究具有Log型惩罚函数的稀疏正则化，给出一种新的非凸变量选择及压缩感知策略，提出一种高效快速阈值迭代算法.并通过变量选择问题和稀疏信号重建验证了所提出的Log型稀疏正则化模型的有效性.

压缩感知；阈值迭代算法；稀疏性

1　引言

高维数据分析是当前统计学、金融经济学、计算机科学和生物信息学等领域面临的主要问题之一.伴随着科学技术的快速发展，各个学科均产生了大批量数据[1].例如在高能物理领域，作为信息技术发展的主要推动者之一，高能物理的实验数据量每年已经超过100PB(千亿万字节，1PB=220GB)，且随着实验规模的不断扩大，实验复杂性的不断增加，现代高能物理产生的海量数据对数据分析研究提出巨大的挑战.例如在生物信息领域，生物技术的进步带来基因组学，蛋白组学，各种组学的出现，使得海量数据的积累变得非常迅速，其中仅个人的基因数据都以GB(千兆字节，1GB=1024MB)作为数据量单位.再比如说在信息技术方向，截止到2012年，数据量已经从TB(万亿字节，1TB=1024GB)级别跃升到PB，EB(百亿亿字节，1EB=1024PB)乃至ZB(十万亿亿字节，1ZB=1024EB)级别.IBM的研究称，整个人类文明所获得的全部数据中，有90%是过去两年内产生的.而到了2020年，全世界所产生的数据规模将达到今天的44倍.从而开展如何有效利用高维海量数据的大数据研究成为了各个科学研究领域面临的挑战与机遇.

稀疏正则化方法是解决高维数据分析的有力工具之一.经典的变量选择方法L0正则化方法最早用于变量选择和特征提取，主要是以参数个数为约束，进而得到最优的变量选择结果.但是L0正则化方法需要求解一个组合优化问题，即NP难问题，难度较大不易实现.1996年，Tibshirani[2]提出了 L1正则化方法，即 Lasso方法.Lasso方法求解的是一个凸优化问题，它在完成变量选择的同时可估计出参数值.从而给出了一种全新的变量选择方法.基于此，Lasso方法在上个世纪90年代后期开始广泛应用于统计学及信号处理等领域.但是，Lasso方法的解不具有一致性，当数据之间有某种强相关性时，不能有效选择正确变量.对于此问题有两种研究方向.其一，研究在何种条件下，Lasso具有解的一致性.此方面研究见文献[3-5].另一种研究方向为如何提出一种新的惩罚函数方法将问题解决，此方面研究见文献[6-9].Candes在文中[3]提出一种加强L1正则化方法，同时给出一种重赋权Lasso方法，并猜测Log型惩罚函数会具有很好的稀疏信号重建能力.

基于Candes的研究工作，本文研究具有Log型的惩罚函数及其快速算法，并通过变量选择和信号重建进行两组实验，说明具有Log型惩罚函数的正则化方法具有有效性.

2　具有 Log型惩罚函数的稀疏正则化方法

本节首先给出一些记号，并给出Log型惩罚函数，并进一步给出一种快速高效的求解方法.

稀疏正则化方法的重大应用领域是稀疏信号重建.为了更好地理解本文的研究方法，下面从稀疏信号重建问题开展研究.其结果可简单推广到其他应用领域.一般地，稀疏信号重建问题描述为：假设有一个有限长度的信号w，w∈RN，该信号在某一个正交基下，表示为w=ϕx，这里ϕ=(ϕ1，···，ϕN)，x称为基的系数.假定通过测量矩阵ψ来对w进行观测(测量)，假定得出的观测值为y，观测噪声为ε，即满足

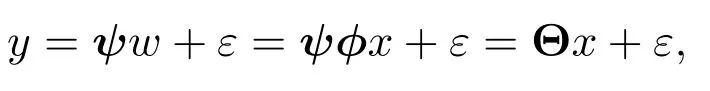
其中，Θ=ψϕ称为传感矩阵.本文希望从观测数据y恢复稀疏未知向量x，进而恢复信号w.

一般地，信号重建问题可以建立如下L0问题的数学模型进行求解：

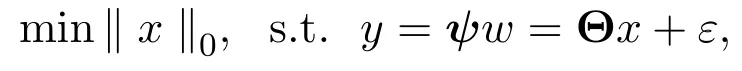
其中∥x∥0为向量x中非零向量的个数.上述模型可以转化为如下正则化表示方法：

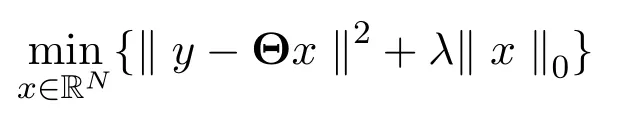
其中x=(x1，···，xN)T∈RN，正则化参数λ＞0.这就是L0正则化方法.L0方法可以产生最稀疏的解，但是需要求解一个NP组合优化问题，所以通常将L0方法转化为下述求解凸优化问题的L1正则化方法：

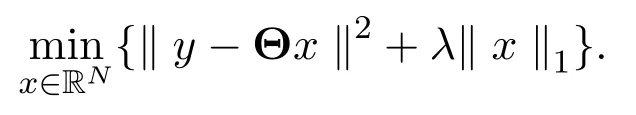
由于 L1正则化方法的求解可以借用现在凸优化的工具，L1正则化成为当今流行的稀疏信号重建策略，并在上世纪 90代后期广泛应用于统计学及信号处理领域.主要代表工作是LASSO(Least Absolute Shrinkage and Selection Operator)[2]和BPDN(Basis Pursuit De-Noising)[10].

虽然L1正则化方法具有凸优化问题中最稀疏的解，但其解仍不够稀疏.同期，Chartrand[11]提出了非凸正则化方法具有更稀疏的解.文献[12]借用相变的工具分析上述压缩感知重建策略的稀疏重建能力，其结果显示，具有非凸罚函数的正则化策略具有更好地稀疏重建能力.基于此，文献[9]提出了L1/2正则化方法，实现了更高效的正则化方法：

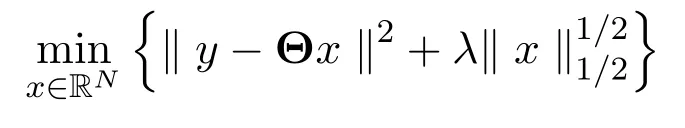
以及张海等提出的基于SCAD方法的压缩感知策略[12].

上述模型可以统一为如下正则化框架进行研究：

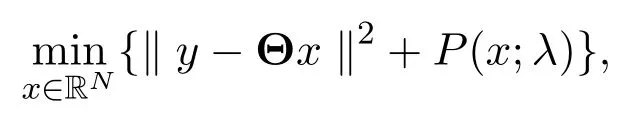
其中P(λ；x)为惩罚函数，λ为正则化参数，用来控制模型的复杂度，从而有效的达到某种优化均衡.

本文研究的Log型稀疏正则化方法的模型如下：

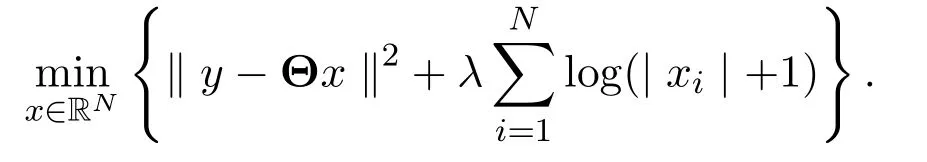
显然，上述模型为非凸正则化问题，其解往往具有更稀疏的结果，如图1所示.

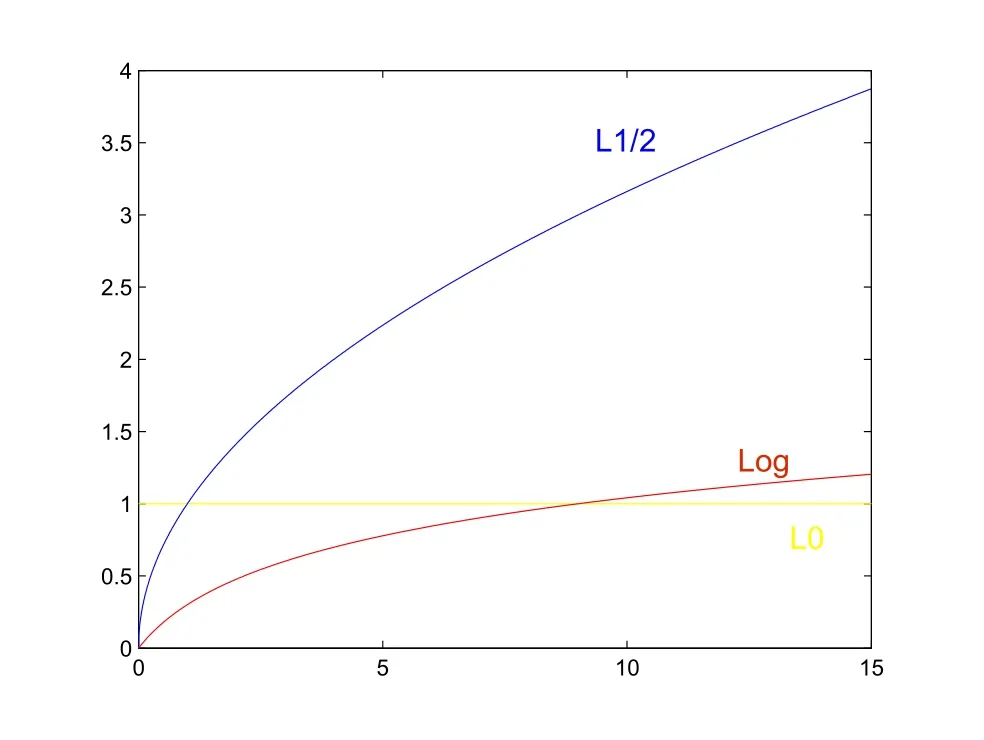
图1　L1，L1/2及Log型稀疏正则化方法解的几何表示

由图1可以看出，Log型正则化方法在无穷远处更平坦，从而更有效逼近L0正则化方法.

3　Log型正则化方法阈值表示理论

阈值迭代算法是一种高效、快速、重建精度高的重构算法，其迭代步骤简单，且可以单分量处理，使得它迅速被大家所认可.阈值迭代算法包括：Blumensath和Davies[13]为求解L0问题而提出的Hard阈值迭代算法，Daubechies等[14]为求解L1(Lasso)[12]问题而提出的Soft阈值迭代算法，徐宗本等[9]提出的求解L1/2的Half阈值迭代算法.

定义3.1如果对于阈值t∗＞0，fd为t的实函数，满足

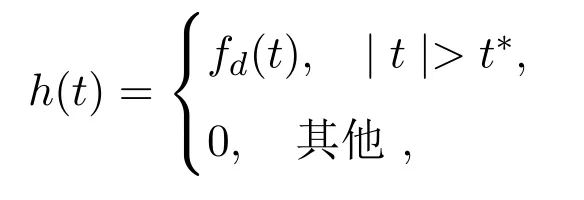
称h为一个阈值函数.由定义可知，阈值函数h是由阈值t和函数fd表达的.

定义3.2若对所有i，hi(x)唯一依赖于xi，并且hi是非线性的，则称映射

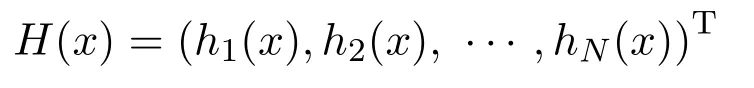
是对角非线性的.

定义3.3当映射H是由阈值函数h得到的，称映射H(x)是阈值算子.

定义 3.4如果一个阈值函数h对正则化问题的任意解x都可以表示成为：

那么称上式为正则化问题的阈值表达.其中，H是由h构成的阈值算子，B是从RN到RN的仿射算子.可以看出，如果正则化问题有阈值表达，则正则化的所有解都可以由算子H和B来表示.

定义3.5如果正则化问题有阈值表达，那么迭代式

称为该正则化问题的阈值迭代算法.

3.1预解算子的表示

Log型正则化的模型如下，

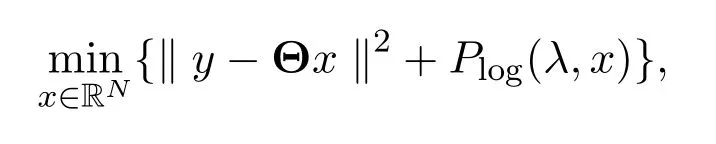
其中

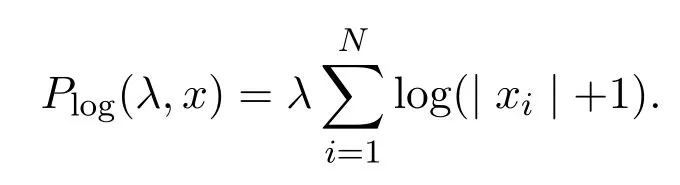
记

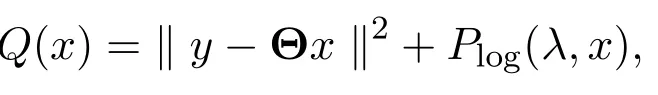
引入变量z，则Q(x)可以整理为：

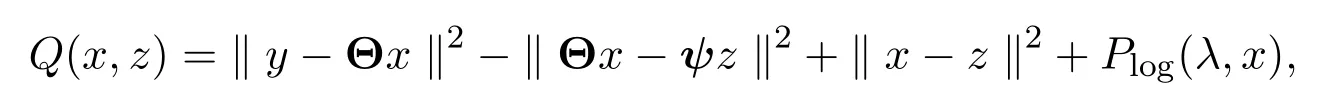
整理得，

当固定变量z时，极小化上式等价于

其中

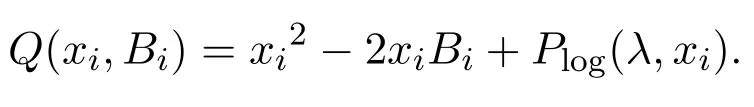
3.2定理及证明

定理3.1极小化问题

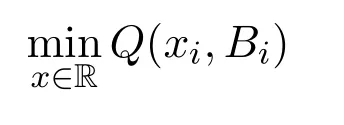
由定理3.1易知，如果函数xi可以有如上表示，那么xi可以看做一个Log型正则化阈值算子用于阈值计算.

证明

3.3 Log型正则化阈值迭代算法

由定理2.1可知，可以设计Log型正则化的阈值算法，

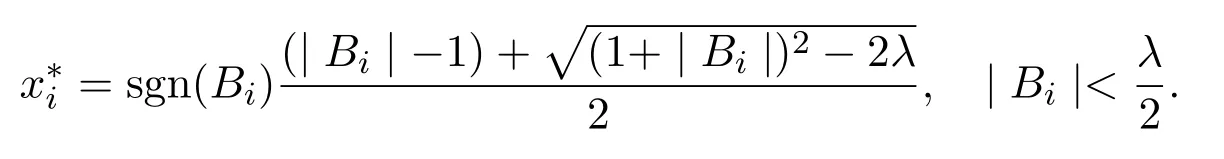
基于Log阈值函数的形式，根据定义5，则Log阈值迭代算法为：

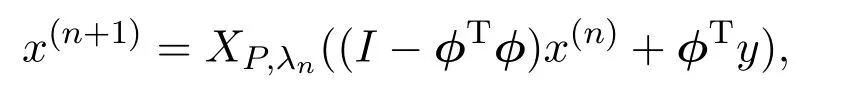
这里λn是第n次迭代的阈值，X(n)是第n次迭代的估计值.

4　实验

本节通过变量选择和稀疏信号重建两个问题说明Log型正则化阈值迭代算法的有效性.

4.1变量选择实验

考虑如下线性模型：

其中

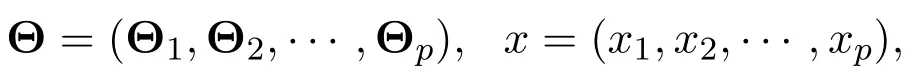
ε为高斯噪声，Eε=0，Dε=σ2.基于上述模型，本实验考虑样本数n=500，训练样本与测试样本比例为1：1的变量选择实验.已知前10个变量不为零，

且Θi=0，10＜i≤p.样本通过高斯随机产生，噪声方差为0.1.在实验中，令维数p从500取至2000.实验比较了Hard，Soft，Half，Log阈值迭代算法以及OMP正交匹配追踪算法.实验结果如图2.实验说明，随着变量维数的增加，Log型正则化阈值迭代方法误差较低，变量选择的准确性较高，与其他几种算法比较优势明显.

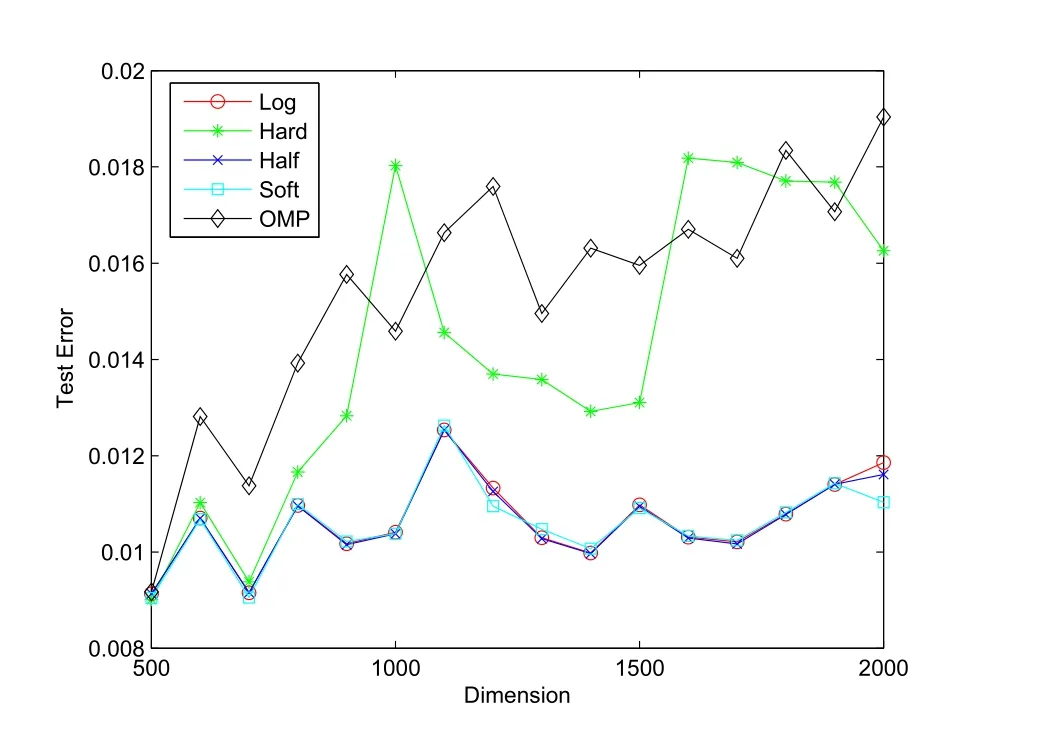
图2　Hard，Soft，Half，Log阈值迭代算法以及OMP正交匹配追踪算法实验结果比较

4.2信号实验

本实验讨论信号为考虑一个信号长度N=256，稀疏度限制k=100的无噪声实值信号x.使用高斯矩阵，取均匀采样数T=180，利用Log型正则化阈值迭代算法，对原始信号进行重建.原始信号图如图3所示，重建信号图如图4所示.信号重建实验说明，Log型罚函数正则化方法较好的重建了原始信号，并可高效实现.

5　结论

高维数据分析是当前热点研究方向之一.由于科学技术的不断发展，各个学科均产生了大量的数据.因此如何有效地从数据中提取信息是诸多学科任务重点之一.基于正则化方法的框架，本文研究具有Log型惩罚函数的稀疏正则化，给出一种新的非凸变量选择及压缩感知策略，并提出相应的高效快速阈值迭代算法.并通过变量选择和稀疏信号重建两组实验，说明了具有Log型惩罚函数的稀疏正则化方法的有效性及算法的准确性.

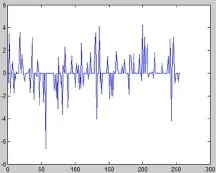
图3　原始信号图

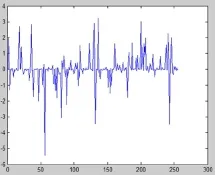
图4　重建信号图

[1]National Research Council of the National Academies.Frontiers in Massive Data Analysis[M].Washington：The National Academies Press，2013.

[2]Tibshiran R.Regression shrinkage and selection via the lasso[J].Journal of the Royal Statistical Society，Series B，1996，58：267-288.

[3]Candes E，Wakin M B，Boyd S.Enhancing sparsity by reweighted minimization[J].IEEE Signal Process. Lett.，2007，14：707-710.

[4]Negahban S，Ravikumar P，Wainwright M J，et al.A unified framework for high-dimensional analysis of M-estimators with decomposable regularizers[J].Statistical Science，2012：27(4)：538-557.

[5]Zhang C H，Huang J.The sparsity and bias of the Lasso selection in high-dimensional linear regression[J]. The Annals of Statistics，2008：36(4)：1567-1594.

[6]Fan J，Li R.Statistical challenges with high dimensionality：Feature Selection in Knowledge Discovery[J]. Proceedings of the International Congress of Mathematicians，European Mathematical Society，2006：595-622.

[7]Zhang C H，Huang J.Nearly unbiased variable selection under minimax concave penalty Annals of Statistics[J].The Annals of statistics，2010：38(2)：894-942.

[8]Zou H.The adaptive lasso and its oracle properties[J].Journal of the American Statistical Association，2006：101，1418-1429.

[9]Xu Z B，Chang X Y，Xu F M，et al.L1/2Regularization：an iterative half thresholding algorithm[J].IEEE Trans.Neural Networks Learning Syst.，2012，23：1013-1027

[10]Chen S，Dohono D，Saunders M.Atomic decomposition by basis pursuit[J].SIAM J.on Sci.Comp.，1998，20：33-61

[11]Chartrand R，Exact reconstructions of sparse signals via nonconvex minimization[J].IEEE Signal Process. Lett.，2007，14：707-710.

[12]张海，梁勇，徐宗本，等.基于SCAD罚函数的有噪压缩感知集[J].数学学报，2013：0583-1431.

[13]Blumensath T.Iterative hard thresholding for compressed sensing[J].Applied and Computational Harmonic Analysis，2009，27(3)：265-274.

[14]Daubechies I，Mefrise M，Mol C.An iterative thresholding algorithm for linear inverse problems with a sparse constraint[J].Communications on Pure and Applied Mathematics，2004，57(11)：1413-1457.

A sparse regularization approach with Log type penalty

Gao Ya，Zhang Hai
(College of Mathematics，Northwest University，Xi′an710127，China)

We study a sparse regularization approach with a Log type penalty function.A new strategy of nonconvex variable selection and compressive sensing is proposed with a alternative thresholding algorithm for fast solution.Then we use variable selection experiment and signal recovery experiment to prove the validity of the sparse regularization with Log type penalty.

compressive sensing，iterative thresholding algorithm，sparsity

O233

A

1008-5513(2015)01-0027-09

10.3969/j.issn.1008-5513.2015.01.004

2014-10-15.

国家自然科学基金(11171272).

高雅(1990-)，硕士生，研究方向：机器学习.

2000 MSC:91D30