诸士金

摘  要：“综合与实践”的题目可以考查学生所积累的数学活动经验，数学应用意识和创新意识是评价数学学科核心素养的重要和有效载体. 文章从关注数学知识与方法的综合、数学文化与知识的结合、数学思维与实验的融合、数学与其他学科知识之间的联系和数学与社会生活的联系五个方面梳理了2021年各地“综合与实践”的典型中考试题，尝试解读了试题的命制意图，并对2022年“综合与实践”中考复习提出适当建议.

关键词：综合与实践;命题分析;核心素养

一、内容分析

2021年全国各地中考试题中“综合与实践”的考查内容和题型在延续往年试题风格的同时，稍有创新. 这里的创新源于近年来发展学生数学学科核心素养的理念渗透，也源于《义务教育数学课程标准（2011年版）》（以下简称《标准》）即将修订的各种解读. 从评价的角度来看，信度与效度较好的“综合与实践”的题目可以考查学生所积累的数学活动经验，数学应用意识和创新意识是评价数学学科核心素养的重要和有效载体. 有利于引导一线教学导向不唯题做题，而要实实在在地开展以理解教学为基础、以理解学生为主体、以理解数学为本质的数学教学活动. 让学生亲历实践、探究、体验、反思、合作、交流等学习过程，综合运用数学学科和跨学科的知识与方法解决现实世界的数学问题.

2021年各地“综合与实践”的中考试题突出关注数学知识与方法的综合、数学文化与知识的结合、数学思维与实验的融合、数学与其他学科知识之间的联系，以及数学与社会生活的联系. 综合考查了学生的直观想象与数学抽象、逻辑推理与数学运算、数学建模与数据分析这六个方面的核心素养. 下面结合部分试题从考查内容的角度进行分类，对“综合与实践”与核心素养评价的立意进行分析.

二、命题思路分析

1. 关注数学知识与方法综合的考查

从概念到判定，从判定到性质，从性质到应用，数学知识之间有着知识结构前后一致、思想方法逻辑连贯的特征. 因此，数学知识的学习是一种学生在已有认知结构的基础上主动认识数学知识结构，并重新建构形成新认知结构的过程. 因此，对学生在数学知识、数学方法上的学习效果和建构的认知程度的评价需要设置结构优良、信度与效度较好的综合试题. 2021年的中考试题中这样的试题秉承了以往的特色，或以代数为主综合考查数学概念、数学运算和建模能力;或以几何为主综合考查几何直观、空间观念和推理能力. 在数学内部从“式”结构到“形”结构，从归纳到推理，从特殊到一般，突出考查分类与模型、数形结合等数学思想与创新意识.

（1）以代数知识为主考查数学概念、数学运算.

例1 （江苏·南通卷）定义：若一个函数图象上存在横、纵坐标相等的点，则称该点为这个函数图象的“等值点”. 例如，点（1，1）是函数[y=12x+12]的图象的“等值点”.

（1）分别判断函数y = x + 2，y = x2 - x的图象上是否存在“等值点”？如果存在，求出“等值点”的坐标;如果不存在，说明理由.

（2）设函数[y=3x]（x > 0），y = -x + b的图象的“等值点”分别为点A，B，过点B作BC⊥Ox，垂足为点C. 当△ABC的面积为3时，求b的值.

（3）若函数y = x2 - 2（x ≥ m）的图象记为W1，将其沿直线x = m翻折后的图象记为W2. 当W1，W2两部分组成的图象上恰有2个“等值点”时，直接写出m的取值范围.

【评析】命题者从所熟悉的一次函数出发，关注到函数图象上的特殊点“等值点”，并由具体的一次函数[y=12x+12]上的等值点联想到其他函数是否存在这样的等值点. 因此，所设计的问题涵盖了一次函数、反比例函数和二次函数. 概念的理解是为了明确研究对象，在明确研究对象的基础上，命题者从概念出发设置问题，考查学生对等值点的深度理解. 在第（2）小题中探究反比例函数和一次函数的等值点的关系. 在第（3）小题中研究二次函数的等值点的个数与函数图象变化之间的关系，皆是对这一概念外延的相關知识的考查. 该题立意开阔，呈现简洁，以一联三，从特殊到一般，数形结合，自然而然.

（2）以几何知识为主考查几何直观、空间观念.

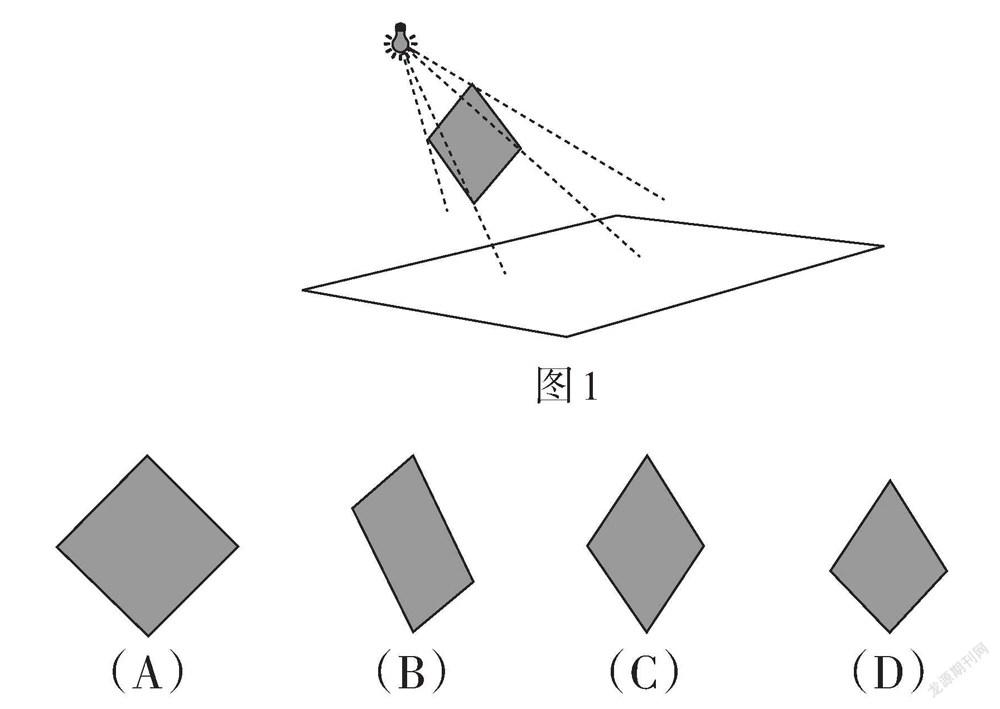
例2 （江苏·南京卷）如图1，正方形纸板的一条对角线垂直于地面，纸板上方的灯（看作一个点）与这条对角线所确定的平面垂直于纸板. 在灯光照射下，正方形纸板在地面上形成的影子的形状可以是

（    ）.

【评析】此题综合考查了特殊四边形的性质、中心投影的相关知识，关注几何直观和空间观念. 试题从“投影”中取材，结合四边形的相关性质成题，背景熟悉而公平，丰富而简洁. 试题四个选项的设计各有特色：A是基于原题中灯光照射对象本身的形状而呈现;B是基于所给平面视角下的正方形纸板的形状而呈现;C是基于正方形与菱形的关系，在“可能”处选择菱形而呈现.

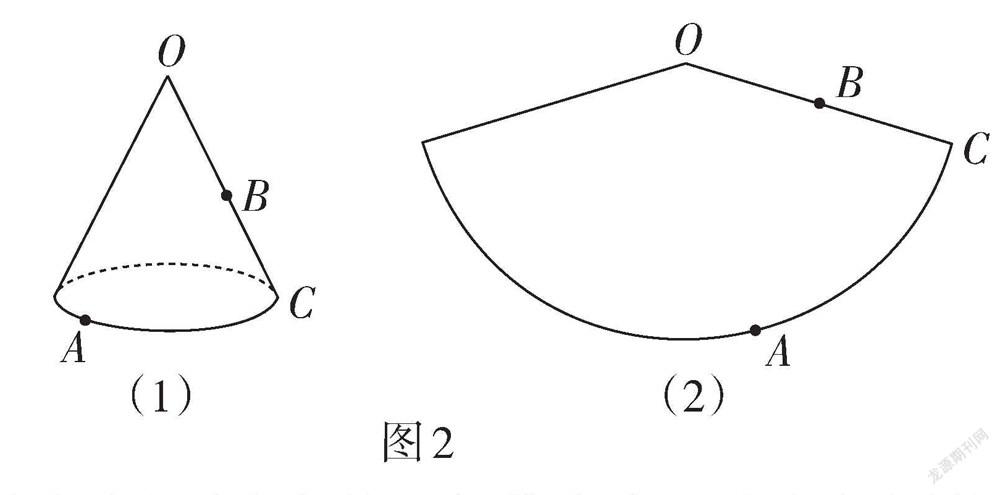
例3 （江苏·南京卷）在几何体表面上，蚂蚁怎样爬行路径最短？

（1）如图2（1），圆锥的母线长为12 cm，B为母线OC的中点，点A在底面圆周上，[AC]的长为4π cm. 在如图2（2）所示的圆锥的侧面展开图中画出蚂蚁从点A爬行到点B的最短路径，并标出它的长（结果保留根号）.

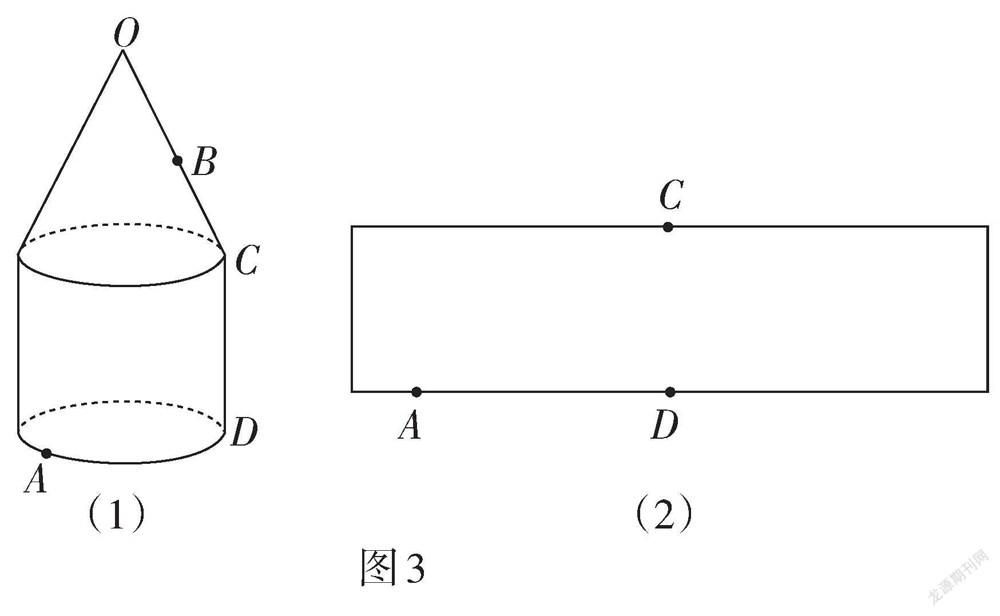
（2）图3（1）中的几何体由底面半径相同的圆锥和圆柱组成. O是圆锥的顶点，点A在圆柱的底面圆周上. 设圆锥的母线长为l，圆柱的高为h.

① 蚂蚁从点A爬行到点O的最短路径的长为

（用含l，h的代数式表示）.

② 设[AD]的长为a，点B在母线OC上，OB = b. 圆柱的侧面展开图如图3（2）所示，在图中画出蚂蚁从点A爬行到点B的最短路径的示意图，并写出求最短路径的长的思路.

【评析】此题综合考查了圆柱和圆锥的展开与折叠、勾股定理、相似三角形的判定与性质、三角函数和方程思想等相关知识. 关注直观想象、数学建模、数学运算等素养，需要学生先通过想象大致感知最短的状态. 其中，写思路来描述思维过程的呈现方式独具一格，目的是跳出机械的运算，重点关注思维的方向和路径. 题目的三道小题之间有一定的层次性. 第（1）小题是圆锥上的最短路径，第（2）小题是特殊化点B的位置. 这两道小题都是第（3）小题的特殊情况. 而学生解答第（3）小题时有困难，但解题思路一脉相承，将立体图形的“最短”转化为平面图形的“最短”，通过让学生画图、写思路，更好地保证试卷的信度和效度.

（3）综合代数几何考查分类讨论、数形结合.

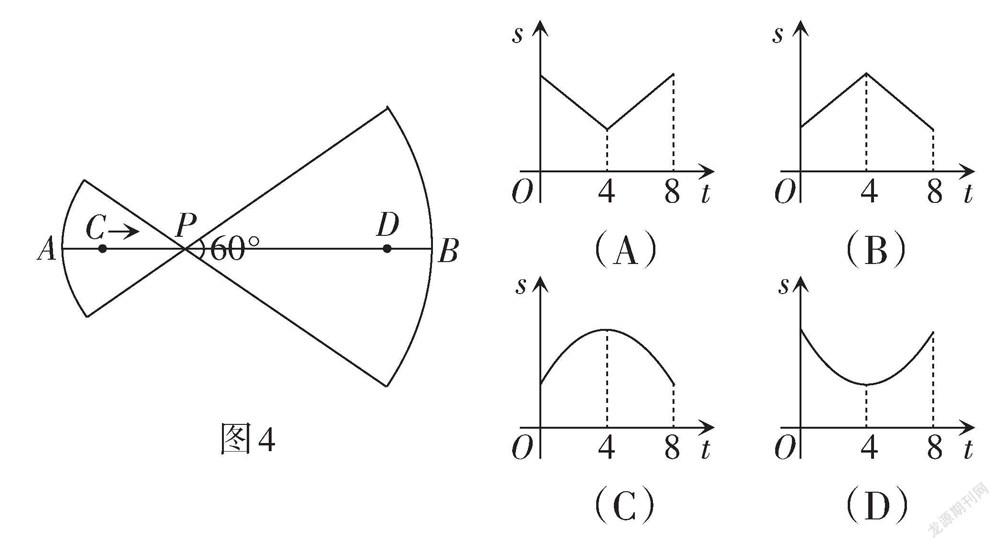
例4 （江苏·苏州卷）如图4，线段AB = 10，点C，D在AB上，AC = BD = 1. 已知点P从点C出发，以每秒1个单位长度的速度沿着AB向点D移动，到达点D后停止移动. 在点P的移动过程中，做如下操作：先以点P为圆心，PA，PB的长为半径分别作两个圆心角均为60°的扇形，再将两个扇形分别围成两个圆锥的侧面，设点P的移动时间为t（单位：秒），两个圆锥的底面面积之和为S，则S关于t的函数图象大致是（   ）.

【评析】此题是动点图象问题，综合考查扇形、圆锥及函数的相关知识. 题目呈现轻巧，由点动到线动，由线动到形变，关注数形结合思想、函数模型思想. 在这一变化中，可研究的变量众多，命题者则是选择了圆锥的底面积之和与运动时间之间的关系进行研究. 一方面，是考查知识的覆盖面所需;另一方面，也是由变量之间关系式的可表达而定.

例5 （江苏·常州卷）【阅读】

通过构造恰当的图形，可以对线段长度、图形面积大小等进行比较，直观地得到一些不等关系或最值，这是数形结合思想的典型应用.

【理解】

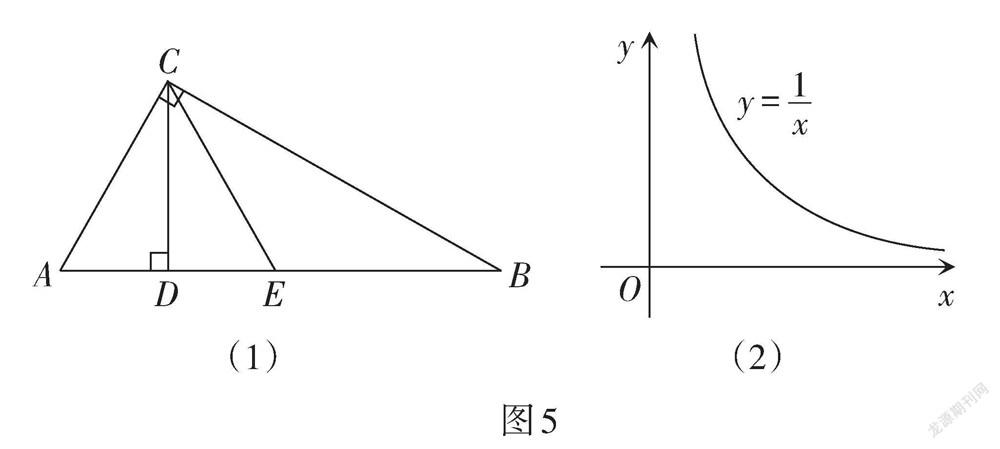
（1）如图5（1），AC⊥BC，CD⊥AB，垂足分别为点C，D，E是AB的中点，连接CE. 已知AD = a，BD = b（0 < a < b）.

① 分别求线段CE，CD的长（用含a，b的代数式表示）;

②比较大小：CE    CD（填“<”“=”或“>”），并用含a，b的代数式表示该大小关系.

【应用】

（2）如图5（2），在平面直角坐标系xOy中，点M，N在反比例函数[y=1x]（x > 0）的图象上，横坐标分别为m，n. 设p = m + n，[q=1m+1n]，记l =[14]pq.

① 当m = 1，n = 2时，l =     ;当m = 3，n = 3时，l =     .

② 通过归纳猜想，可得l的最小值是     . 试利用图5（2）构造恰当的图形，并说明你的猜想成立.

【评析】此题属于反比例函数综合题，综合考查了反比例函数的性质、相似三角形的判定和性质、直角三角形斜边中线的性质等知识. 命题者从“数缺形时少直观，形缺数时难入微”进行立意，以阅读理解的形式呈现问题，直指“数形结合”，从简入繁，从三角形中特殊线段长度的研究到反比例函数k的几何意义的理解，从归纳猜想到验证说理，将以数定形、以形助数的价值凸显出来，关注到直观想象、逻辑推理等数学学科核心素养的考查.

2. 关注数学文化与知识结合的考查

在近年来的各地中考试题中，出现了一些数学文化融入评价中的导向，这一尝试促使数学的学习更具开阔的视野，凸显了数学文化的育人价值. 在具体的试题命制中呈现的特色主要体现在两个方面：与数学趣味素材相结合、与数学史相结合. 这些试题对命题的要求极高，命题者既要关注到素材的公平性，保障试题的信度，又要关注到素材的取舍和处理，体现较好的效度. 因此，多数试题的尝试还有待进一步研究和創新.

例6 （贵州·安顺卷）（1）阅读理解.

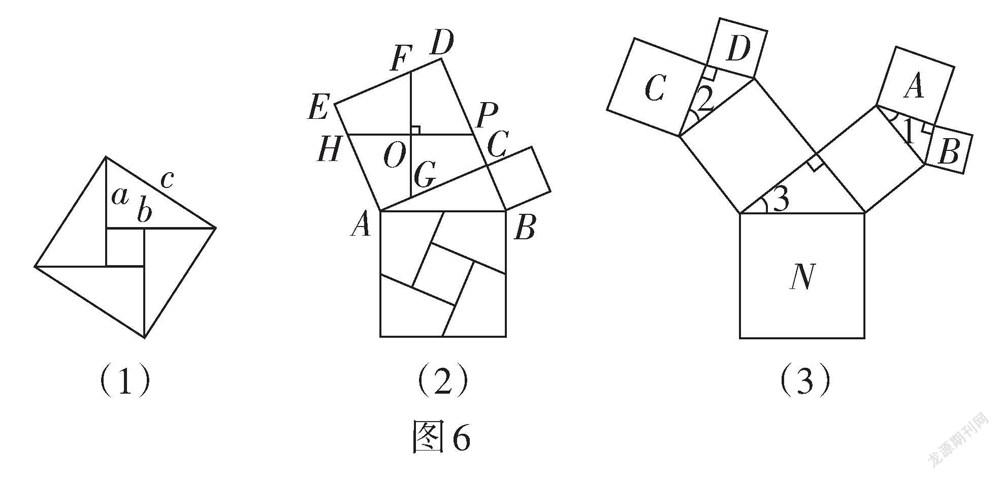
我国是最早了解勾股定理的国家之一，它被记载于我国古代的数学著作《周髀算经》中. 汉代数学家赵爽为了证明勾股定理，创制了一幅如图6（1）所示的“弦图”，后人称之为“赵爽弦图”.

根据“赵爽弦图”写出勾股定理和推理过程.

（2）问题解决.

勾股定理的证明方法有很多，图6（2）是古代的一种证明方法：过正方形ACDE的中心O，作FG⊥HP，将它分成4份，所分成的四部分和以BC为边的正方形恰好能拼成以AB为边的正方形. 若AC = 12，BC = 5，求EF的值.

（3）拓展探究.

如图6（3），以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程就可以得到“勾股树”的部分图形. 设大正方形N的边长为定值n，小正方形A，B，C，D的边长分别为a，b，c，d.

已知∠1 = ∠2 = ∠3 = α，当角α（0° < α < 90°）变化时，探究b与c的关系式，并写出该关系式及解答过程（b与c的关系式用含n的式子表示）.

【评析】此题从“赵爽弦图”出发，综合考查了正方形的性质、全等三角形的性质、勾股定理的证明、相似三角形的判定与性质等知识. 需要学生先明白根据“赵爽弦图”推理勾股定理的方法，再以此为基础进行拓展探究. 这里的拓展探究体现命题者对“勾股树”特征研究的独特见解，将相似三角形的知识藏于其中，引导学生发现c + b = n这样的规律，彰显了数学文化的影响力. 此题关注了对学生几何直观、空间观念和逻辑推理能力的考查.

3. 关注数学思维与实验融合的考查

基于数学实验进行评价一直是“综合与实践”考查的主要方式. 试题呈现往往需要学生经历观察、操作、探索、验证、反思来体现数学思考的过程. 既注重外显的操作表达，更注重头脑中的内隐认知、思想领悟和意义建构. 这些试题的特征大体以几何素材为背景，需要学生运用直观感知、操作确认、推理论证、度量计算等认识图形，并探索图形的性质，确定图形的形状、大小和位置关系. 常常以剪拼、折叠及旋转等变化方式呈现.

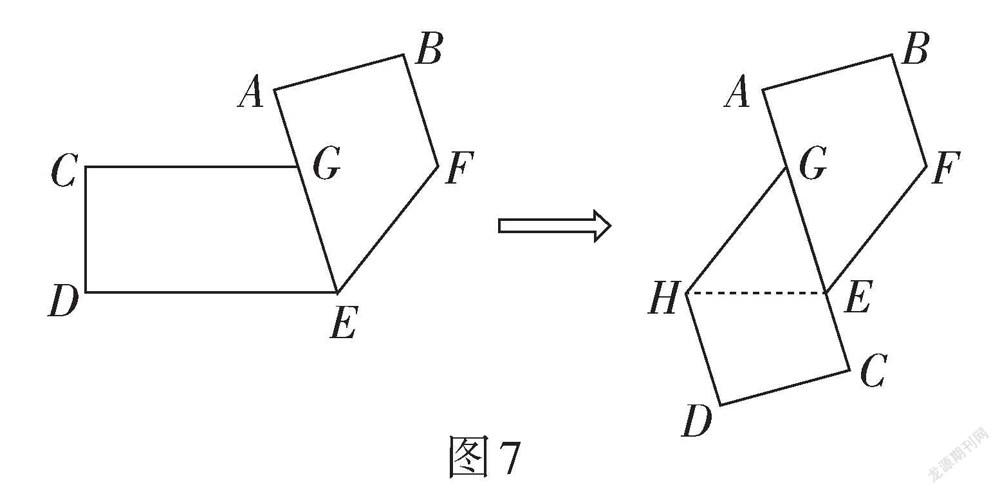
例7 （山东·威海卷）如图7，先将矩形纸片ABCD沿EF折叠（边AB与DE在CF的异侧），AE交CF于点G;再将纸片折叠，使CG与AE在同一条直线上，折痕为GH. 若∠AEF = α，纸片宽AB = 2 cm，则HE =         .

【评析】此题是常见的折纸问题，综合考查了轴对称的性质、平行四边形的判定与性质、矩形的性质、锐角三角函数，需要学生在感知图形变化中确定研究对象. 命题者将折叠的纸片从一次折叠突破到二次折叠，是折纸问题的延伸. 两次折叠后的要求是“使CG与AE在同一条直线上”，这里给予了问题建构的空间. 命题者在这一特定要求下赋予角度和线段长度，引出关于HE长度与∠AEF角度关系的思考. 这里采用α表示，并没有给出具体度数，避免特殊角度影响试题的效度，更体现了这个角度与HE长度的一般关系. 此题关注了几何直观、空间观念和逻辑推理能力的考查.

例8 （黑龙江·齐齐哈尔卷）数学实践活动是一种非常有效的学习方式，通过活动可以激发我们的学习兴趣，提高动手、动脑能力，拓展思维空间，丰富数学体验，让我们一起动手来折一折、转一转、剪一剪，体会活动带给我们的乐趣.

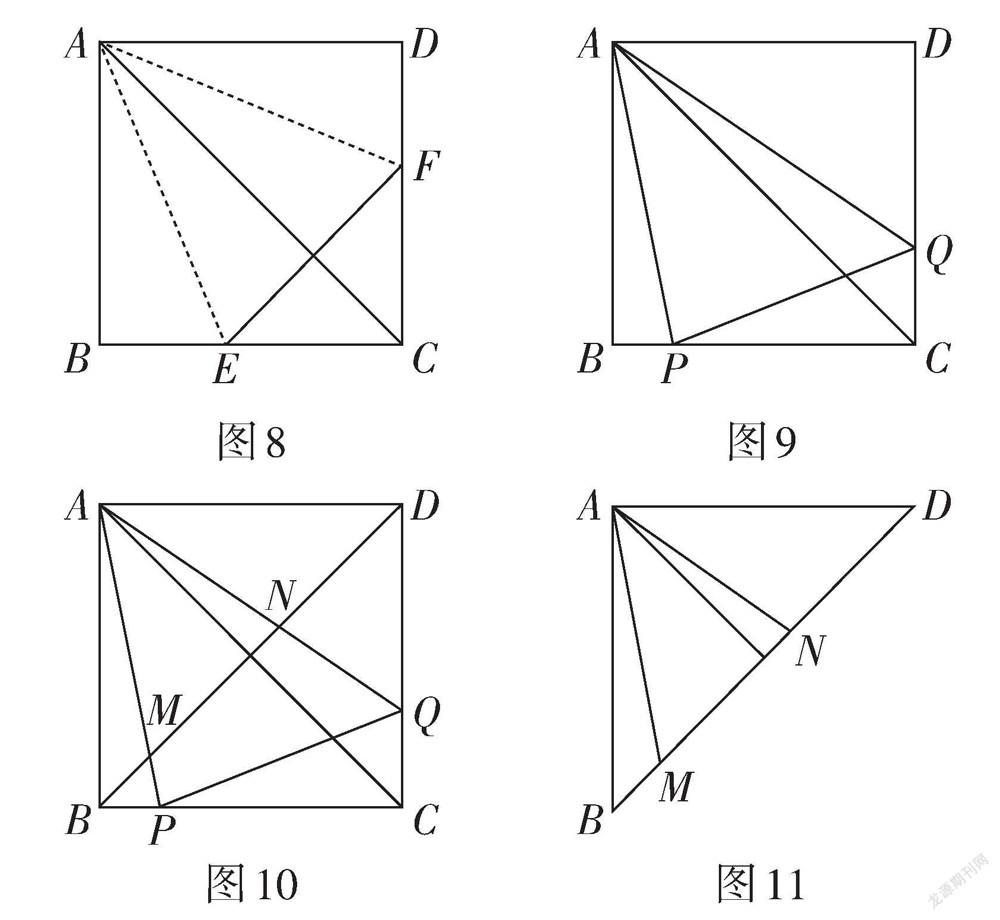
折一折：将正方形纸片ABCD折叠，使边AB，AD都落在对角线AC上，展开得折痕AE，AF，连接EF，如图8所示.

（1）∠EAF =       ，写出图中两个等腰三角形     （不需要添加字母）.

轉一转：将图8中的∠EAF绕点A旋转，使它的两边分别交边BC，CD于点P，Q，连接PQ，如图9所示.

（2）线段BP，PQ，DQ之间的数量关系为    .

（3）连接正方形对角线BD，若图9中的∠PAQ的边AP，AQ分别交对角线BD于点M，N，如图10所示，则[CQBM]=     .

剪一剪：将图10中的正方形纸片沿对角线BD剪开，如图11所示.

（4）求证：BM2 + DN2 = MN2.

【评析】此题从“折一折、转一转、剪一剪”的角度综合考查了正方形的性质、全等三角形的判定和性质、勾股定理、相似三角形的判定和性质等知识，需要学生在各种实验操作的基础上经历观察、想象、操作与思考. 此题从折纸开始，关注到对折到正方形纸片对角线处所形成的角和图形的形状的特殊性. 这一步引入是学生比较熟悉而且容易理解的操作，学生可以借助手中的素材直接操作验证得到. 在“折一折”之后，命题者从运动的角度切入，以折得的角为研究对象，进行“转一转”，引发线段之间关系的探究. 两道小题，一道小题考查全等三角形，一道小题考查相似三角形，相得益彰.“剪一剪”跳出了正方形框架，以独特的视角看图形变化. 一方面，是常见数学实验操作的必然呈现，从折、转到剪，丰富了实验操作的内容;另一方面，是图形生长的自然趋势，从图8到图9是由特殊到一般，由定到变;从图9到图10是基于图形元素之间的关联，逐步“枝繁叶茂”;从图10到图11则是分解重组，推陈出新，构建新的图形结构. 此题的整体立意巧妙，内部关联紧密，关注了对学生几何直观、空间观念、逻辑推理等能力的考查，渗透数形结合、特殊到一般的数学思想，体现“做中学”这一综合与实践开展的价值.

4. 关注数学与其他学科联系的考查

跨学科主题是培养学生的创新意识、合作精神、实践能力和社会责任感的一种综合性探究学习方式. 近年来，从《标准》修订到教材修改，从教学到评价，都在关注数学与其他学科之间的联系. 评价什么、如何评价及学科联系之间的程度如何确定等问题成为了评价尝试的重点和创新点. 因此，需要命题者从学科整合的情境出发设计合理的问题，考查学生综合运用数学学科和跨学科的知识与方法来解决问题的能力. 当前跨学科的评价试题还不够多，内容涉及其他学科还不够丰富，常与物理、化学、生物、体育、信息等学科进行联系，与其他学科乃至多个学科关联的综合型问题有待开发.

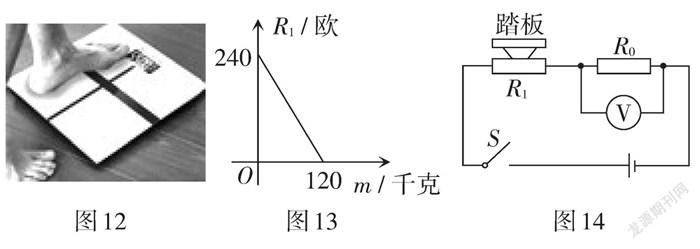
例9 （浙江·台州卷）如图12所示的电子体重秤读数直观又便于携带，为人们带来了方便. 某综合实践活动小组设计了简易电子体重秤：制作一个装有踏板（踏板质量忽略不计）的可变电阻R1，R1与踏板上人的质量m之间的函数关系式为R1 = km + b（其中k，b为常数，0 ≤ m ≤ 120），其图象如图13所示;图14的电路中，电源电压恒为8伏，定值电阻R0的阻值为30欧，接通开关，人站上踏板，电压表显示的读数为U0，该读数可以换算为人的质量m.

温馨提示：① 导体两端的电压U，导体的电阻R，通过导体的电流I，满足关系式I =[UR];

② 串联电路中电流处处相等，各电阻两端的电压之和等于总电压.

（1）求k，b的值;

（2）求R1关于U0的函数解析式;

（3）用含U0的代数式表示m;

（4）若电压表量程为0 ～ 6伏，为保护电压表，试确定该电子体重秤可称的最大质量.

【评析】此题以物理中的电路问题为背景，综合考查了一次函数、反比例函数等相关知识，关注到数形结合思想，体现了对数学运算、数学建模能力的考查. 试题需要学生在理解物理知识的基础上，确定函数关系式. 第（4）小题可以应用反比例函数的增、减性，也可以将m与U0的关系式转化为关于m的不等式，再代入0 ≤ U0 ≤ 6中，求出电子体重秤可称的最大质量m. 此题与物理学科知识紧密联系，其中“温馨提示”具有人文性，也避免了学生对个别物理知识的理解不同对数学综合应用考查的效度影响.

5. 关注数学与社会生活联系的考查

数学知识与现实世界是紧密联系的，在现实世界中用数学眼光观察问题，用数学思维思考问题和解决问题是数学学科的素养体现，是认识、理解、表达现实世界的工具、方法和语言. 因此，结合数学课程内容和问题解决的真实需要，设计恰当的综合主题和探究任务进行评价，考查学生亲历实践、探究、体验、反思、合作、交流等学习过程所获取的数学经验是各地中考长久以来的评价重点. 多年来，创设问题情境体现应用意识的试题层出不穷，涵盖了我们生活的方方面面，但设计的评价试题如何能考查学生综合运用数学知识与方法解决现实世界的数学问题一直是所有人追求的方向.

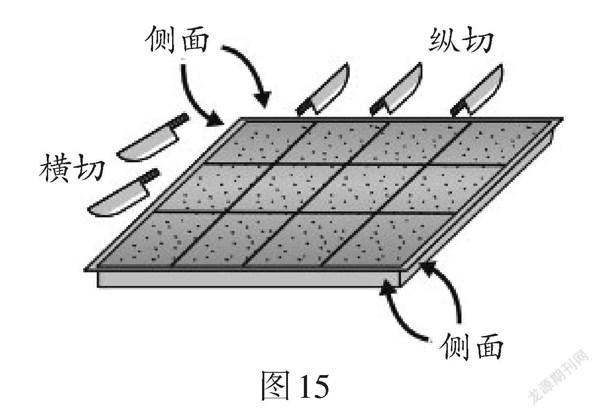
例10 （台湾卷）凯特平时常用底面为矩形的模具制作蛋糕，并以平行于模具任一边的方式进行横切或纵切，横切都是从模具的左边切割到模具的右边，纵切都是从模具的上边切割到模具的下边. 用这种方式，可以切出数个大小完全相同的小块蛋糕. 在切割后，他发现小块蛋糕接触模具的地方外皮比较焦脆.  以图15为例，横切2刀，纵切3刀，共计5刀，切出（2 + 1） × （3 + 1） = 12个小块蛋糕，其中侧面有焦脆的小块蛋糕共有10个，所有侧面都不焦脆的小块蛋糕共有2个.

试根据上述切割方式，回答下列问题，并详细解释或完整写出你的解题过程.

（1）若对一块蛋糕切了4刀，则可切出几个小块蛋糕？试写出任意一种可能的蛋糕块数即可.

（2）今凯特根据一场聚餐的需求，打算制作出恰好60个所有侧面都不焦脆的小块蛋糕，为了避免劳累并加快出餐速度，在不超过20刀的情况下，试问凯特需要切几刀，才可以达到需求？写出所有可能的情形.

【评析】此题以“制作蛋糕”的实际生活背景为素材，综合考查规律探究、方案设计等知识，需要学生积累生活经验，将实际问题数学化，渗透了对几何直观、数形结合和分类讨论思想的综合考查. 试题素材贴近学生，问题的呈现由易到难，凸显真实性.

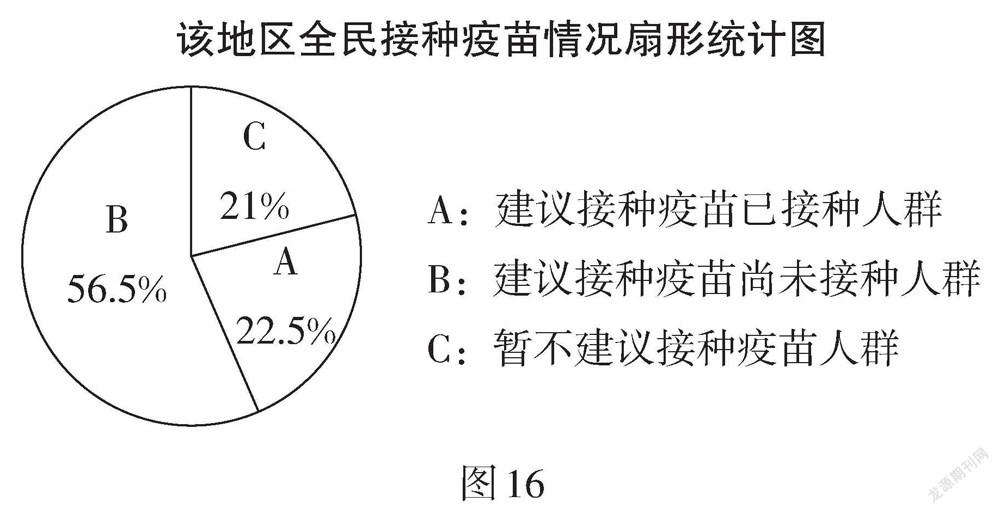
例11 （江苏·盐城卷）为了防控新冠肺炎疫情，某地区积极推广疫苗接种工作，卫生防疫部门对该地区八周以来的相关数据进行收集整理，绘制得到对应图表如图16、表1所示.

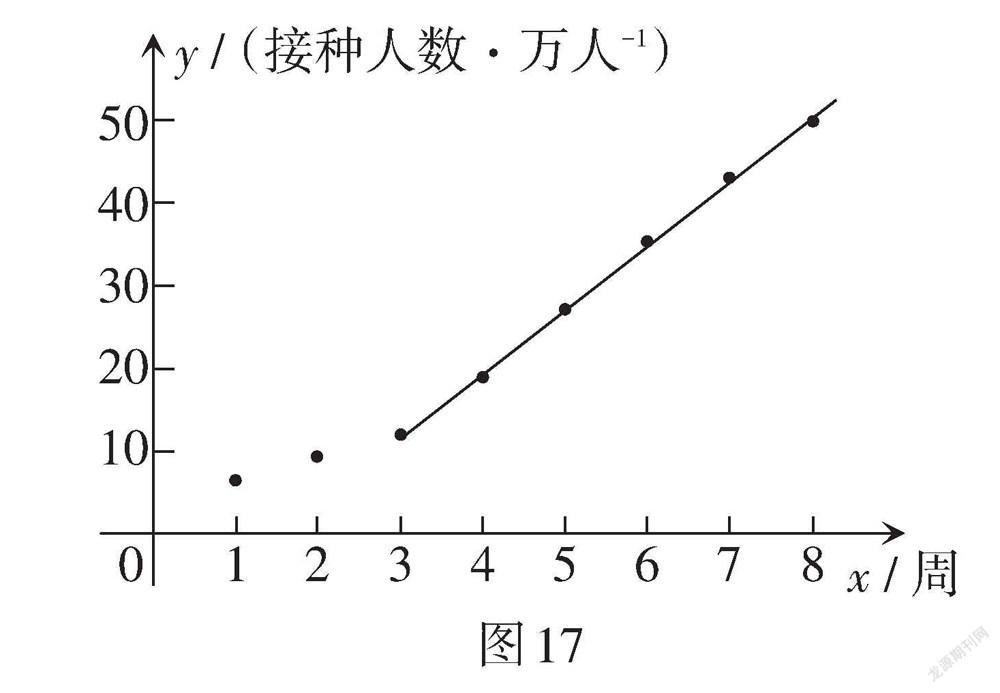
根据统计表1中的数据，建立以周次为横坐标，接种人数为纵坐标的平面直角坐标系，并根据以上统计表中的数据描出对应的点，发现从第3周开始这些点大致分布在一条直线附近，现过其中两点（3，12），（8，42）作一条直线（如图17，该直线的函数表达式为y = 6x - 6），那么这条直线可近似反映该地区接种人数的变化趋势.

试根据以上信息，解答下列问题：

（1）这八周中每周接种人数的平均数为       ;该地区的总人口约为       .

（2）若从第9周开始，每周的接种人数仍符合上述变化趋势.

① 估计第9周的接种人数约为       ;

② 專家表示：疫苗接种率至少达60%才能实现全民免疫. 那么，从推广疫苗接种工作开始，最早到第几周，该地区可达到实现全民免疫的标准？

（3）实际上，受疫苗供应等客观因素影响，从第9周开始接种人数将会逐周减少a（a > 0）万人，为了尽快提高接种率，一旦周接种人数低于20万人时，卫生防疫部门将会采取措施，使得之后每周的接种能力一直维持在20万人. 如果a = 1.8，那么该地区的建议接种人群最早将于第几周全部完成接种？

【评析】此题关注社会热点问题，以防控新冠肺炎疫情推广疫苗接种为背景取材，立意积极向上，数据科学真实. 综合考查了一次函数的应用、平均数、不等式等相关知识. 对平均数的考查需要学生理解并提取表格信息，关注学生信息提取能力的考查;第（2）小题的设计则是基于已有的表格信息，结合拟合的一次函数考查一次函数的应用，体现以数据说话进行“估计”的价值;第（3）小题则是进一步在一次函数理解的基础上融入不等式，考查不等式模型的建立. 命题者将这些素材的数学立意围绕“疫苗接种”进行设计，既有梯度，又有效度，考查了学生解决实际问题的能力，体现了对“会用数学眼光观察世界，会用数学思维思考世界，会用数学语言表达世界”的数学学科核心素养的评价.

三、复习建议

综合与实践是帮助学生积累数学活动经验、培养应用意识和创新意识、提升数学学科核心素养的重要和有效载体. 多年来，一直是全国中考试题关注的重点，更是落实立德树人、进行学科育人评价的难点. 各区域的命题在不断改革和创新，呈现出更具综合性、真实性、科学性和时代性的特征. 综合与实践的试题主要评价学生在理解数学知识结构的基础上，重新建构数学认知的完善程度、方法路径以及经验获取的转化、迁移能力;考查学生通过运算、推理进行归纳、演绎得到新的结论，解决与其他学科、与生活紧密联系的问题;引导学生在学习和评价中体会数学知识的价值，以及与其他学科知识的关联. 基于此，针对2022年中考，关于综合与实践的复习提出以下几点建议.

1. 整体把握课程目标，系统复习综合实践

为了使每名学生都受到良好的数学教育，数学教学不仅要使学生获得数学知识技能，而且要把“知识技能”“数学思考”“问题解决”“情感态度”四个方面有机结合，整体实现课程目标. 因此，综合与实践能力的提升不在于做多少试题，而在于解决问题的能力，需要细化分解，有针对性地进行专题复习，夯实基础运算、基本技能. 例如，针对函数综合试题，可以选择一个有效的载体串起多类型函数知识，将函数图象与性质进行关联;在综合复习中可以尝试以“模块化”进行设计. 例如，围绕“垂直”串起初中所有与这一特殊位置关系有关联的知识;在综合与实践中常见的分类思想、模型思想和数形结合思想可以选择方案设计、图形变化、问题解决等类型试题进行巩固……所以，教师要重视对教学内容的整体分析，了解数学知识的产生与来源、结构与关联、价值与意义，并以此进行中考复习. 因此，中考复习需要系统设计，从整体课程目标出发，合理安排时间，科学选择专题.

2. 深挖数学文本资源，拓宽学生数学视野

理解数学从理解《标准》、深读教材文本开始. 一线数学教师有必要深度理解数学教材的编写意图，关注数学文本中丰富的资源. 在教材中，综合与实践的内容多数是融入课时学习中进行的，也有一部分是以课题学习、数学活动、数学实验室等形式突出体现. 在平时教学和中考复习中要将这些综合与实践的素材理解到位，分析各地区综合与实践的试题与文本资源的关联程度，选择有效的同类型载体，进一步挖掘文本资源可拓展的空间. 例如，探寻勾股数组中所体现出来的代数推理的价值，折纸活动中所体现出来的几何直观和逻辑推理能力，等等. 在深挖文本资源的同时，建议适当拓宽学生的数学视野，选择贴近学生生活的素材培养其数学的眼光，有利于他们经历从现实情境中抽象出数学知识与方法. 所选择的素材要关注到生活现实、数学现实和其他学科现实. 这些素材应考虑到学生的最近发展区，应揭示学科知识的内在联系，体现数学学科的整体性;应尽量选择来源于生活、社会中的现象和问题，体现数学学科的应用性;应巧妙地与其他学科之间建立联系，体现数学学科的基础性. 具体呈现方式则在符合学生认知需求的同时，更有助于学生理解数学的本质，引发学生深入思考，以使学生感受到数学的趣味、价值和意义.

3. 创新数学教学方式，重视学生主体地位

数学知识的形成及逐渐完善的过程中往往蕴含着一定的数学思想. 好的教学方式有利于促进学生自主探索，引发学生认知冲突，激发学生学习动机. 在综合与实践的复习教学中，不宜文本化教学，不宜题海式解题、讲题. 需要引发学生积极的数学思考，让学生在问题解决中体验成功的快乐. 例如，组织可操作的折纸实验、测量活动、阅读欣赏等形式促进学生共同进行设疑、质疑、释疑的数学活动，帮助学生养成良好的学习习惯，促进学生学会学习.

多年来，综合与实践的评价如何更好地落实立德树人、学科育人的任务是所有命题者的不懈追求. 正确看待评价的测量功能，认识到评价的价值导向才能更有利于一线教学关注学生的数学理性精神的培育，促进学生数学学科核心素养的发展.

四、模拟题欣赏

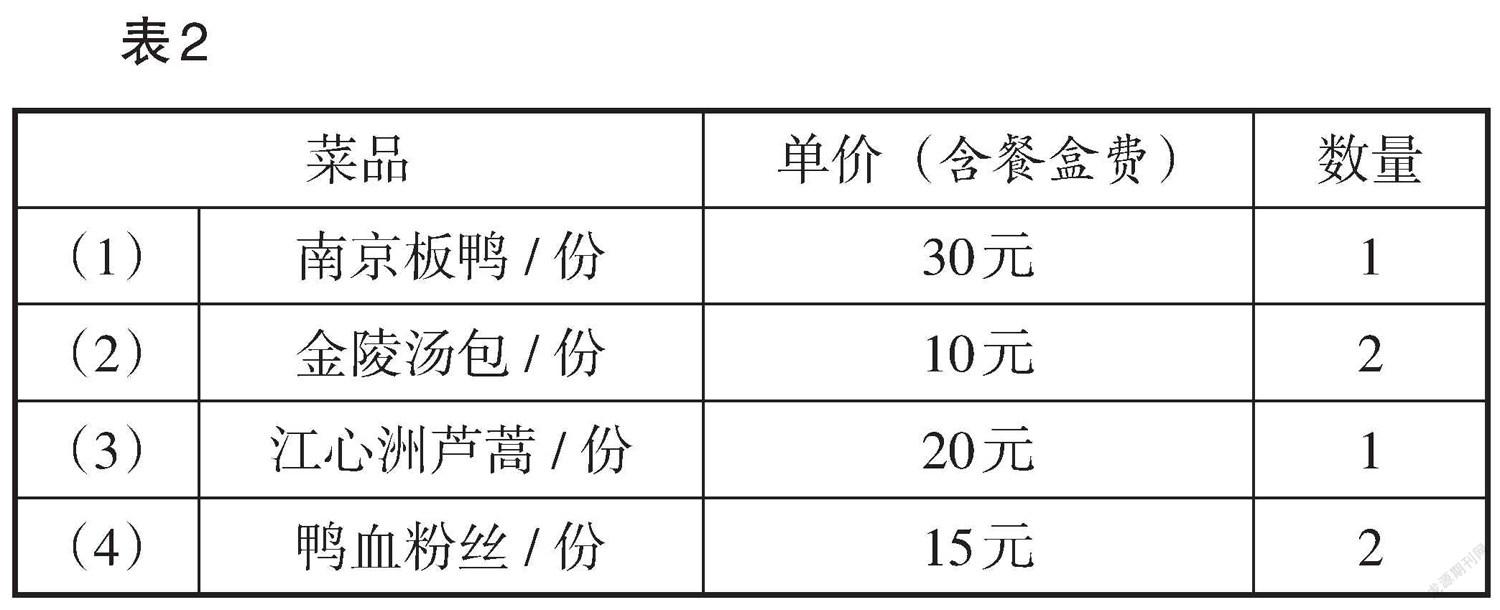
1. 小宁计划在某外卖网站下单购买如表2所示的菜品. 已知每份订单的配送费为3元，商家为了促销，对每份订单的总价（不含配送费）提供满减优惠：满30元减15元，满60元减35元，满80元减40元，满100元减45元. 如果小宁在购买表2中的任意三项菜品时，采取适当的下订单方式，那么他点餐的总费用优惠幅度最大可为         .

答案：44元.

2.【学习理解】

定义：平面上与已知线段两个端点连接而形成直角三角形的点我们称为已知线段的“勾股点”. 若一个点是两条已知线段的“勾股點”，则该点为这两条线段的“公共勾股点”.

【概念巩固】

（1）如图18，已知在Rt△ABC中，AC = 3，BC = 4，∠C = 90°. 试借助尺规在边BC所在直线上确定点P，使得点P为AB的“勾股点”，并求PC的长.

（2）若点P为（1）中Rt△ABC两边AB，BC的公共“勾股点”，则PC的最大值为      .

【深入研究】

（3）如图19，已知△ABC，P为AB和BC的公共“勾股点”. 连接PB交AC于点Q，若点Q恰好是AB和BC的另一个公共“勾股点”. 求证：△ABC为等腰三角形.

【直观猜想】

（4）是否存在一个点P和△ABC，使得P为△ABC三边的公共“勾股点”. 如果存在，画出示意图;如果不存在，说明理由.

答案：（1）如图20所示;PC =[94].

（2） 5.

（3）证明略.

（4）存在，如直角三角形（如图21）.

3. 定义：一般地，对两个封闭图形甲、乙，若甲的顶点都在乙的边界上，则称甲是乙的内接图形，乙是甲的外接图形（图形甲的边可以和图形乙的边重合）.

已知，在△ABC中，∠ACB = 90°，AC = 2，BC = 3. 如图22，矩形DEFG是△ABC的外接矩形，正方形BCHI是△ABC的外接正方形，等边三角形JKL是△ABC的外接等边三角形.

显然，一个图形的外接多边形不唯一，我们可以探索△ABC的最小外接多边形.

（1）试在图23中分别画出△ABC的最小外接矩形、最小外接正方形、最小外接等边三角形的示意图，并直接写出它们的边长.

（2）类似地，用一张等边三角形纸片剪一个直角边长分别为1 cm和3 cm的直角三角形纸片，等边三角形纸片的边长最小是多少？画出示意图，并写出这个最小值.

答案：（1）① 如图24（1），矩形ACBE是△ABC的最小外接矩形，AC = 2，BC = 3;

② 如图24（2），正方形MNBQ是△ABC的最小外接正方形，边长为[91010];

③ 如图24（3），等边三角形ABP是△ABC的最小外接等边三角形，边长为[13].

（2）如图25，等边三角形AMN即为所求，边长为[3010+91010]cm.

参考文献：

[1]中华人民共和国教育部制定. 义务教育数学课程标准（2011年版）[M]. 北京：北京师范大学出版社，2012.

[2]教育部基础教育课程教材专家工作委员会. 《义务教育数学课程标准（2011年版）》解读[M]. 北京：北京师范大学出版社，2012.