白瑞蒲,李晓娟

(河北大学 数学与信息科学学院， 河北 保定 071002)

3-李代数[1]在几何、物理等方面都发挥了重要作用[2-3], 因此, 3-李代数的研究受到人们的广泛关注[4-6]. Lie-Rinehart代数作为李代数胚的几何概念中的代数部分被人们所熟知[7]. 1997 年, Huebschmann 给出了Lie-Rinehart代数的概念, 并研究了其在李代数胚上的作用[8]. 之后许多学者对Lie-Rinehart代数的结构及应用进行了研究[9-10]. Mandal[11-12]等定义了Hom-Lie-Rinehart代数, 并研究了其低维扩张问题.本文要对3-Lie-Rinehart 代数[3]的导子和交叉模的结构进行研究.

除特别声明以外, 文章讨论的代数和向量空间的基域F的特征为零,A是F上的交换结合代数,V为F上的向量空间.

1 预备知识

3-李代数L是具有线性运算[,,]:L＾ 3→L的向量空间[1],满足∀x1,x2,x3,y2,y3∈L,

[[x1,x2,x3],y2,y3]=[[x1,y2,y3],x2,x3]+
[[x2,y2,y3],x3,x1]+[[x3,y2,y3],x1,x2].

(1)

设L是F上的3-李代数,如果F-线性映射D∶L→L满足∀x,y,z∈L,D[x,y,z]=[Dx,y,z]+[x,Dy,z]+[x,y,Dz],则称D是L的导子,L的导子李代数记为Der(L).

由式(1),对∀x,y,z∈L,左乘映射adx,y∶L→L,adx,yz=[x,y,z]及其线性组合是导子,称为内导子,且满足∀x1,x2,y1,y2∈L,[adx1,y1,adx2,y2]=ad[x1,y1,x2],y2+adx2[x1,y1,y2].内导子李代数记为ad(L).

对F线性映射ρ∶L∧L→gl(V),若有下列等式成立∀xi∈L,1≤i≤4,

[ρ(x1,x2),ρ(x3,x4)]=ρ([x1,x2,x3],x4)-ρ([x1,x2,x4],x3),

ρ([x1,x2,x3],x4)=ρ(x1,x2)ρ(x3,x4)+ρ(x2,x3)ρ(x1,x4)+ρ(x3,x1)ρ(x2,x4),

则称(V,ρ)是3-李代数L的表示,简称(V,ρ)为L-模[4].子空间Kerρ={x∈L|ρ(x,L)=0}称作ρ的核.

由式(1)可知,对任意3-李代数L,(L,ad)是3-李代数L的表示,称为L的正则表示,其中∀x,y∈L,ad∶L∧L→gl(L),ad(x,y)=adx,y，且Kerad=Z(L)={x∈L|[x,L,L]=0}.

定义1[10]设L是李代数,且L是A-模,(A,ρ)是L-模.如果ρ(L)⊆Der(A),并且

[x,az]=a[x,z]+ρ(x)az,ρ(ax)=aρ(x),∀x,z∈L,a∈A,

(2)

则称(L,ρ)为李-Rinehart代数.若ρ=0,则L叫作李-A代数.

定义2[13]设域F上的3-李代数L是A-模,(A,ρ)是L模,且满足ρ(L∧L)⊆Der(A),

[x,y,az]=a[x,y,z]+ρ(x,y)az,ρ(ax,y)=ρ(x,ay)=aρ(x,y),∀x,y,z∈L,a∈A,

则称(L,A,ρ)为3-李-Rinehart代数.进一步,若ρ=0,则(L,A)为3-李A-代数.

定义3[13]设(L,A,ρ)和(L′,A,ρ′)是3-李-Rinehart代数,f∶L→L′是3-李代数同态.如果f满足

f(ax)=af(x),ρ′(f(x),f(y))=ρ(x,y),∀a∈A,x,y∈L,

(3)

则称f为3-李-Rinehart代数同态.进一步,如果f是双射,则称f是同构映射;如果f是满射并且Ker(f)⊆Z(L),则称f为中心满态.

定义4[13]设(L,A,ρ)是3-李-Rinehart代数,(R,A)是3-李A-代数,β∶L∧L→Der(R)是F-线性映射. 如果满足:

1)(R,β)是3-李代数L-模；

2)β(ax,y)=β(x,ay)=aβ(x,y),∀a∈A,x,y∈L；

3)β(x,y)(ar)=aβ(x,y)r=β(x,y)(a)r,∀a∈A,r∈R,x,y∈L.

则称β是(L,A,ρ)在(R,A)上的作用. 进一步, 如果R是Abel 的, 即[R,R,R]=0, 则称(R，β)是 3-李-Rinehart 代数(L,A,ρ)-模.

引理1[13]设(L,A,ρ)是3-李-Rinehart代数, 则(L∧L,ρ2)是李-Rinehart 代数, 其中

(4)

ρ2∶L∧L→Der(A),ρ2(x∧y)=ρ(x,y),∀x∧y∈L∧L.

(5)

引理2[13]设(L,A,ρ)是3-李-Rinehart代数, (R,A)是Abel 3-李A-代数,(R,β)是3-李代数L-模，则(R,β)是(L,A,ρ)-模当且仅当(L+βR,A,ρ4)是3-李-Rinehart代数,其中3-李代数L+βR的运算为∀x1,x2,x3∈L,r1,r2,r3∈R,

[x1+r1,x2+r2,x3+r3]=[x1,x2,x3]+β(x1,x2)r3+β(x2,x3)r1+β(x3,x1)r2,

(6)

ρ4∶(L+βR)∧(L+βR)→Der(A),ρ4(x1+r1,x2+r2)=ρ(x1,x2).

(7)

2 3-李-Rinehart代数到3-李A-代数的导子

定义5设(L,A,ρ)是3-李-Rinehart代数, (R,A)是Abel 3-李A-代数,β∶L∧L→Der(R)是(L,A,ρ)在(R,A)上的作用. 如果F-线性映射ψ∶L→R满足

ψ([x,y,z])=[ψ(x),ψ(y),ψ(z)]+β(x,y)ψ(z)+β(y,z)ψ(x)+β(z,x)ψ(y),∀x,y,z∈L,

(8)

则称ψ是从(L,A,ρ)到(R,A)的3-李-Rinehart代数导子. 记Derβ(L,R)为从(L,A,ρ)到(R,A)的3-李-Rinehart 代数导子的全体.

(9)

(10)

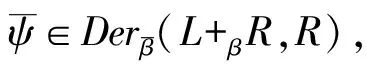
ψ(x,r)∶L+βR→R,ψ(x,r)(z+r′)=β(z,x)r∀z∈L,r∈R.

(11)

定理3设(L,A,ρ)和(L′,A,ρ′)是3-李-Rinehart代数,(R,β)是(L,A,ρ)-模. 如果f∶L′→L是3-李-Rinehart代数同态,则对∀ψ∈Derβ(L,R),有ψ′=ψf∈Derβ′(L′,R)成立(简称ψ为f-A-导子),并且(R,β′)是由f诱导的(L′,A,ρ′)-模,其中

β′∶L′∧L′→gl(R),β(x′,y′)=β(f(x′),f(y′)),∀x′,y′∈L′.

(12)

证明：由式(8), 对∀x′,y′,z′∈L′,得到

ψ′([x′,y′,z′])=[ψf(x′),ψf(y′),ψf(z′)]+β(f(x′),f(y′))ψ(f(z′))+
β(f(y′),f(z′))ψ(f(x′))+β(f(z′),f(x′))ψ(f(y′))=
[ψ′(x′),ψ′(y′),ψ′(z′)]+β′(x′,y′)ψ′(z′)+β′(y′,z′)ψ′(x′)+β′(z′,x′)ψ′(y′).

因此,ψ′∈Derβ′(L′,R).由定理2, 易知(R,β′)是(L′,A,ρ′)-模. 证毕.

定理4设(L,A,ρ)和(L′,A,ρ′)是3-李-Rinehart代数,(R,β)是(L,A,ρ)-模,则对任意3-李-Rinehart 代数同态f∶L′→L和任意f-A-导子ψ′∈Derβ′(L′,R),存在唯一3-李-Rinehart代数同态h∶L′→L+R满足

π·h=f,q·h=ψ′,

(13)

其中,π∶L+βR→L,π(x+r)=x;q∶L+R→R,q(x+r)=r,∀x∈R.

反之, 对任意3-李-Rinehart代数同态h∶L′→L+R,则存在唯一3-李-Rinehart代数同态f∶L′→L和唯一f-A-导子,满足式(13), 其中β′由式(12)定义.

证明：设f∶L′→L是3-李-Rinehart 代数同态,则由定理3 可知,(R,β′)是由f诱导的3-李-Rinehart 代数(L′,A,ρ′)-模. 对∀ψ′∈Derβ′(L′,R), 定义F-线性映射

h′∶L′→L+R,h(x′)=f(x′)+ψ′(x′),∀x′∈L′,

(14)

则π·h(x′)=f(x′), 且q·h(x′)=ψ′(x′). 因此,h满足式(13).

再由定义3，引理2，式(8)和式(14), 对∀a∈A,x′,y′,z′∈L′有

h(ax′)=f(ax′)+ψ(ax′)=a(f(x′)+ψ′(x′))=ah(x′),
h([x′,y′,z′])=[f(x′)+ψ′(x′),f(y′)+ψ′(y′),f(z′)+ψ′(z′)]=[h(x′),h(y′),h(z′)].

所以h是3-李代数同态,且ρ4(h(x′),h(y′))=ρ4(f(x′)+ψ′(x′),f(y′)+ψ(y′))=ρ′(x′,y′).因此,h是3-李-Rinehart代数同态.

反之,设h′∶L′→L+R是3-李-Rinehart代数同态. 定义f∶L′→L和ψ′∶L′→R为

f(x′)=π(h(x′)),ψ′(x′)=q(h(x′)),∀x′∈L′.

因此,对∀x′∈L′,有f=π·x,ψ′=q·h所以式(13)成立.

根据引理2, 对∀x′,y′z′∈L′,a∈A有ρ4(h(x′),h(y′))=ρ′(x′,y′)=ρ(f(x′),f(y′)),f(ax′)=af(x′),ψ′(ax′)=aψ′(x′),其中ρ4由式(7)定义, 并且h([x′,y′,z′])=[h(x′),h(y′),h(z′)]=f([x′,y′,z′])+ψ′([x′,y′,z′]).所以f([x′,y′,z′])=[f(x′),f(y′),f(z′)],ψ′([x′,y′,z′])=[ψ′(x′),ψ′(y′),ψ′(z′)]+β′(x′,y′)ψ′(z′)+β′(y′,z′)ψ′(x′)+β′(z′,x′)ψ′(y′).因此,f∶L′→L是3-李-Rinehart代数同态,并且ψ′∈Derβ′(L′,R).证毕.

3 3-李-Rinehart代数的交叉模

定义6设(L,A,ρ)是3-李-Rinehart代数,(R,A)是3-李A-代数,β∶L∧L→Der(R)是3-李-Rinehart代数(L,A,ρ)在(R,A)上的作用,如果3-李代数同态∂∶R→L满足

1)∂(β(x,y)r)=[x,y,∂r],∀r∈R,x,y∈L；

2)β(∂r1,∂r2)r=[r1,r2,r],∀r1,r2,r∈R；

3)β(x,∂r1)r2=-β(x,∂r2)r1,∀r1,r2∈R；

4)∂(ar)=a∂(r),∀a∈A,r∈R；

5)ρ(∂(r1),∂(r2))(a)=0,∀a∈A,r1,r2,r∈R.

则称(R,A,β,∂)为3-李-Rinehart 代数(L,A,ρ)的交叉模.

定理5设(L,A,ρ)和(L′,A,ρ′)是3-李-Rinehart代数,f∶L′→L是3-李-Rinehart代数同态,∂∶Ker(f)→L是包含映射,即对∀u∈Ker(f),有∂(u)=u.则(Ker(f),A,ad,∂)是3-李-Rinehart 代数(L,A,ρ)的交叉模.

证明：由定义4可知,ad∶L∧L→Der(Ker(f))是(L,A,ρ)在(Ker(f),A)上的作用.对∀x,y∈L,u1,u2∈Ker(f)和a∈A, 有

∂(adx,yu)=adx,yu=[x,y,u],∂(au)=au=a∂(u),ad∂u1,∂u2u=[u1,u2,u],
adx,∂u1u2=[x,∂u1,u2]=-adx,∂u2u1,ρ(∂(u1),∂(u2))(a)=ρ′(f(u1),f(u2))a=0,

所以,(Ker(f),A,ad,∂)满足定义6. 证毕.

例1由定义6和定理5可知,对3-李-Rinehart代数(L,A,ρ),若N是(L,A,ρ)的真理想,则(N,a,ad,i)是3-李-Rinehart代数(L,A,ρ)的交叉模,其中i∶N→L,i(x)=x,∀x∈N.若(R,β)是(L,A,ρ)-模, 则(R,A,β,0)是(L,A,ρ)的交叉模.

定理6设(L,A,ρ)是3-李-Rinehart代数,(R,A)是3-李A-代数,∂∶R→L是3-李-Rinehart的中心满态,则(R,A,β,∂)是(L,A,ρ)的交叉模,其中β∶L∧L→gl(R),

β(x,y)r=[r1,r2,r],且∂(r1)=x,∂(r2)=y,∀x,y∈L,r1,r2,r∈R.

(15)

证明：因为∂∶R→L是3-李-Rinehart代数的中心满态,由定义3可知,∂是3李-Rinehart代数同态,并且满足Ker(∂)⊆Z(R)和∂(R)=L.因此,β由式(15)定义有意义,且∀a∈A,r,r1,r2∈R,有∂(ar)=a∂(r)和ρ(∂(r1),∂(r1))(a)=0.由式(1)和(15),对∀x,y∈L,ri∈R,1≤i≤5,存在r1,r2∈R,使得∂(r1)=x,∂(r2)=y,并且

β(x,y)[r3,r4,r5]=[r1,r2,[r3,r4,r5]]=[β(x,y)r3,r4,r5]+[r3,β(x,y)r4,r5]+[r3,r4,β(x,y)r5],
β(x,∂r3)∂r4=[r1,r3,r4]=-[r1,r4,r3]=-β(x,∂r4)∂r3,
β(∂r1,∂r2)r=β(x,y)r=[r1,r2,r],∂(β(x,y)r)=∂[r1,r2,r]=[∂r1,∂r2,∂r]=[x,y,∂r].

因此,(R,A,β,∂)满足定义6.证毕.

定理7设(L,A,ρ)是3-李-Rinehart代数,(R,A)是3-李A-代数,(R,A,β,∂)是(L,A,ρ)的交叉模,则下面结论成立.

1)(Im(∂),A,ρ|Im(∂)∧Im(∂))是(L,A,ρ)的次理想;

2)(Coker(∂),A是3-李A-代数, 其中ρ0(Coker(∂),Coker(∂))=0;

3)(Ker(∂),A)是(R,A)的Abel理想;

4)(L,A,ρ)在(R,A)上的作用β诱导了(Im(∂),A,ρ|Im(∂)∧Im(∂))在(Ker(∂),A)上的作用β|Im(∂)∧Im(∂).

证明：由定义 6可知,Im(∂)是L的子代数,并且对∀r∈R,x,y∈L和a∈A,有a∂(r)=∂(ar)∈Im(∂),[x,y,∂r]=∂(β(x,y)r)∈Im(∂).因此,(Im(∂),A,ρ|Im(∂)∧Im(∂))是(L,A,ρ)的次理想,则结论1)得证. 结论2)可由结论1)直接推得.

因为∂∶R→L是3-李代数同态, 所以Ker(∂)是3-李代数R的理想.对∀r∈R,r1，r2,r′∈Ker(∂),a∈A,有∂(ar′)=a∂(r′)=0,[r1,r2,r]=β(∂(r1),∂(r2))r=0.因此,Ker(∂)是A-模, 并且[Ker(∂),Ker(∂),R]=0, 则结论3)得证. 结论4)根据定义6和结论1)可直接推得. 证毕.

设(L,A,ρ)是3-李-Rinehart代数,R=L∧L(向量空间)是李A-代数, 且(L,A,ρ)满足

ρ(x,y)bz=0,∀x,y,z∈L,b∈A.

(16)

记

(17)

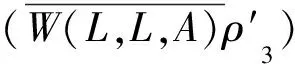
(18)

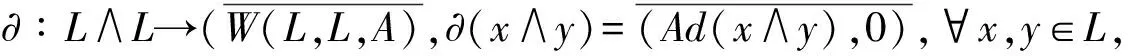
(19)

并且Ad(x∧y)∈Der(R),Ad(x∧y)(x′∧y′)=[x∧y,x′∧y′],∀x′∧y′∈R.进一步,Ker(∂)是李代数L∧L的中心,Ker(∂)是A-模.