相对于模N的完全不变子模F的N-投射模
2022-07-06王永铎杜晓微
王永铎,杜晓微
(兰州理工大学 理学院,甘肃 兰州 730050)
在本文中,R都是有单位元的结合环,所有的模都是右R-模.N⊆M表示N是M的子集,N≤M表示N是M的子模,N◁M表示N是M的完全不变子模,N≤⊕M表示N是M的直和项,EndR(M)表示模M的自同态环,HomR(M,N)表示M到N的同态集,E(M)、Rad(M)、Soc(M)和τ(M)分别表示右R-模M的内射包、根、基座和预根.I、Rad(R)和τ(R)分别表示环R的理想、根和预根.
投射模是模论和同调代数中的三大重要模类之一,关于投射模的研究是同调代数最基本也是最核心的内容.随着同调代数的发展,国内外很多数学家开始从事投射模的推广工作,他们从不同的角度对投射模进行了推广,得到了很多重要的概念[1-5],丰富了投射模的理论体系.2012年有学者提出了τ-N-投射模和τ-投射模的概念[1].设M和N是右R-模.称M是τ-N-投射模,若对任意满同态f:N→L和任意同态h:M→L,其中L是N/τ(N)的像(等价于τ(N)⊆kerf),存在同态g:M→N使得h=fg.称M是τ-投射模,若M是τ-RR-投射的.2013年,Amin等[2]提出了Rad-N-投射模和Rad-投射模的概念,并用它们刻画了半完备环、完备环等重要的环类.以上研究对经典的投射模做了很好的推广,对丰富投射模理论做出了贡献.受文献[1-7]的启发,为了统一上述概念,本文很自然地考虑将上述概念中的τ(N),Rad(N)换为N的任意完全不变子模去研究,进而引入相对于模N的完全不变子模F的N-投射模和相对于理想I的R-投射模的概念.设M,N是右R-模,F◁N.称M是相对于模N的完全不变子模F的N-投射模,若对任意满同态f:N→L和任意同态h:M→L,其中L是N/F的像(等价于F⊆kerf),存在同态g:M→N使得h=fg.显然,当F=0时,相对于模N的完全不变子模F的N-投射模是N-投射模;当F=τ(N)时,相对于模N的完全不变子模F的N-投射模是τ-N-投射模;当F=Rad(N)时,相对于模N的完全不变子模F的N-投射模是Rad-N-投射模;当F=N时,任意右R-模都是相对于模N的完全不变子模F的N-投射模.本文研究了相对于模N的完全不变子模F的N-投射模和相对于理想I的R-投射模的一些基本性质,统一了N-投射模,τ-N-投射模和Rad-N-投射模的一系列结论.

定义1设M,N是右R-模,F◁N.称M是相对于模N的完全不变子模F的N-投射模,若对任意满同态f:N→L和任意同态h:M→L,其中L是N/F的像(等价于F⊆kerf),存在同态g:M→N使得h=fg.
注1设M,N是右R-模,F◁N.当F=0时,相对于模N的完全不变子模F的N-投射模是N-投射模;当F=τ(N)时,相对于模N的完全不变子模F的N-投射模是τ-N-投射模;当F=Rad(N)时,相对于模N的完全不变子模F的N-投射模是Rad-N-投射模;当F=N时,任意右R-模都是相对于模N的完全不变子模F的N-投射模.
命题1设M,N是右R-模,F◁N.则下列条件等价:
1)M是相对于模N的完全不变子模F的N-投射模;
2) 如果f:N→L是满同态,其中L是N/F的像,那么f*:HomR(M,N)→HomR(M,L)是满同态,其中f*(α)=fα,α∈HomR(M,N);
3) 每个同态β:M→N/K,其中F⊆K≤N,都可通过自然满同态v:N→N/K分解.
证明1)⟹2) 设M是相对于模N的完全不变子模F的N-投射模且f:N→L是满同态,其中L是N/F的像.因为M是相对于模N的完全不变子模F的N-投射模,所以对任意同态g∈HomR(M,L)都存在同态α∈HomR(M,N)使得f*(α)=fα=g,故f*是满同态.
2)⟹1)⟹3) 显然.
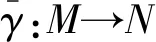

图1 交换图Fig.1 Commutative diagram
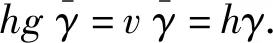
命题2设M,N是右R-模,F◁N.则以下几条成立.
1) 若M=⊕i∈IMi,则M是相对于模N的完全不变子模F的N-投射模当且仅当每个Mi(i∈I)是相对于模N的完全不变子模F的N-投射模.
2) 若A,B是右R-模且A≅B,A是相对于模N的完全不变子模F的N-投射模当且仅当B是相对于模N的完全不变子模F的N-投射模.
3) 设K/F◁N/F.若M是相对于模N的完全不变子模F的N-投射模,则M是相对于模N/F的完全不变子模K/F的N/F-投射模.
证明1) “⟹”考虑图2.
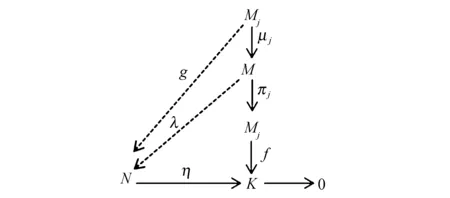
图2 交换图Fig.2 Commutative diagram
其中μj是标准嵌入,πj是自然投影,F⊆kerη.因为M是相对于模N的完全不变子模F的N-投射模,所以存在λ:M→N使得ηλ=fπj.因为ηλμj=fπjμj=f,取g∶=λμj,所以ηg=f.故Mj(j∈I)是相对于模N的完全不变子模F的N-投射模.
“⟸”考虑图3.

图3 交换图Fig.3 Commutative diagram
其中F⊆kerη.因为Mj是相对于模N的完全不变子模F的N-投射模,所以存在同态λj:Mj→N使得ηλj=fμj.由直和的泛性质可知存在唯一同态θ:Μ→N使得θμj=λj,故ηθμj=ηλj=fμj,由θ的唯一性可知ηθ=f.因此M是相对于模N的完全不变子模F的N-投射模.
2) 考虑图4.

图4 交换图Fig.4 Commutative diagram
其中F⊆kerη.因为A是相对于模N的完全不变子模F的N-投射模,所以存在λ:Α→Ν使得ηλ=fθ.因为ηλθ-1=fθθ-1=f,取g∶=λθ-1:B→N,所以ηg=f.因此B是相对于模N的完全不变子模F的N-投射模.反之同理.
3) 假设M是相对于模N的完全不变子模F的N-投射模,K/F◁N/F且K/F⊆H/F≤N/F.考虑图5.
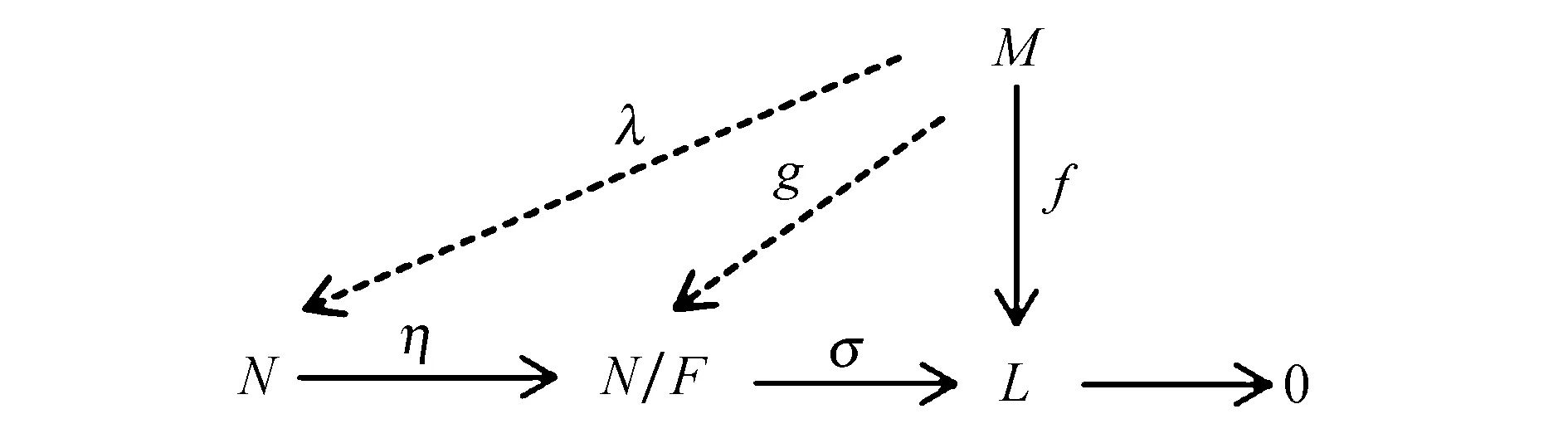
图5 交换图Fig.5 Commutative diagram
其中σ:N/F→L是自然满同态,其中L=((N/F)/(K/F))/((H/F)/(K/F)).因为η是自然满同态,所以F=kerη⊆kerση=H.因为M是相对于模N的完全不变子模F的N-投射模,所以存在同态λ:M→N使得σηλ=f,取g∶=ηλ,则σg=f,故M是相对于模N/F的完全不变子模K/F的N/F-投射模.

证明只需证n=2时结论成立.当n=2时,设f:N1⊕N2→(N1⊕N2)/K是自然满同态,其中F1⊕F2⊆K.考虑下列行列正合的交换图6.
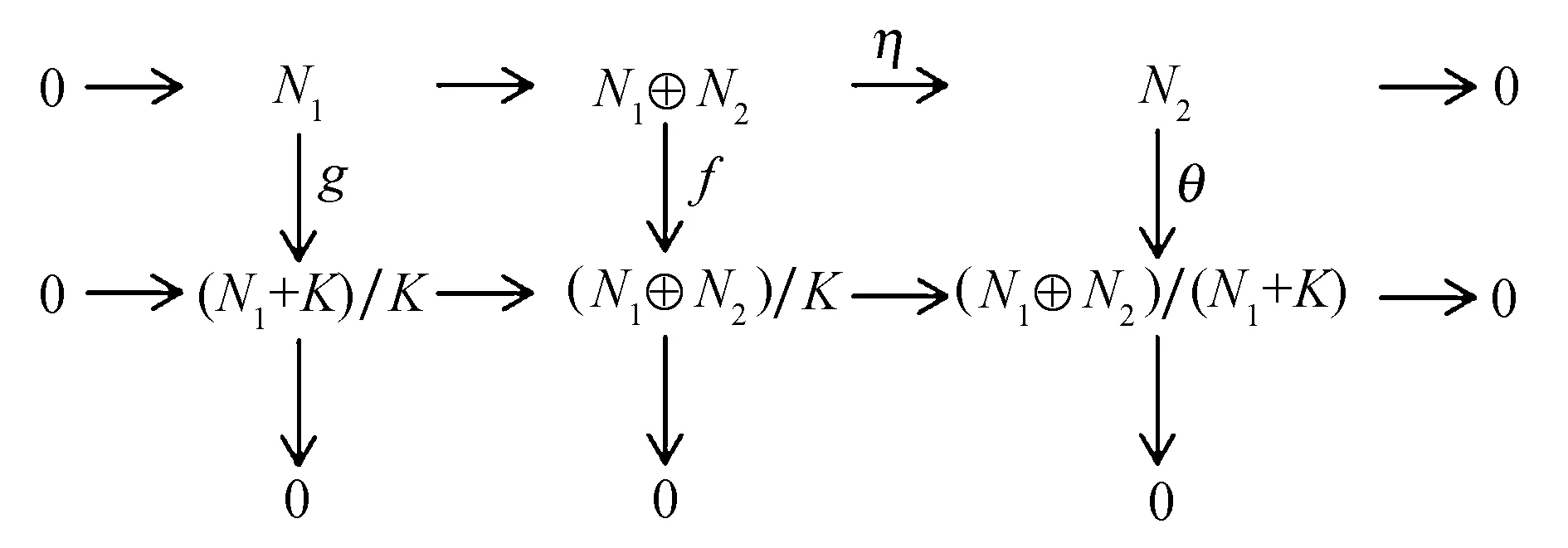
图6 交换图Fig.6 Commutative diagram
其中θ:N2→(N1⊕N2)/(N1+K),θ(n2)=n2+N1+K,n2∈N2,显然θ是满同态.用Hom(M,-)作用图6可得图7.

图7 交换图Fig.7 Commutative diagram
其中g*α=gα,α∈Hom(M,N).因为F1⊆N1∩K=kerg,F2⊆(N1+K)∩N2=kerθ且M是相对于模Ni的完全不变子模Fi的Ni-投射模(i=1,2),所以由命题1中2)可知g*,θ*是满同态.因为Hom函子保持可裂正合性,所以η*是满同态,从而f*是满同态.因此M是相对于模N1⊕N2的完全不变子模F1⊕F2的N1⊕N2-投射模.
最后,考虑图8.
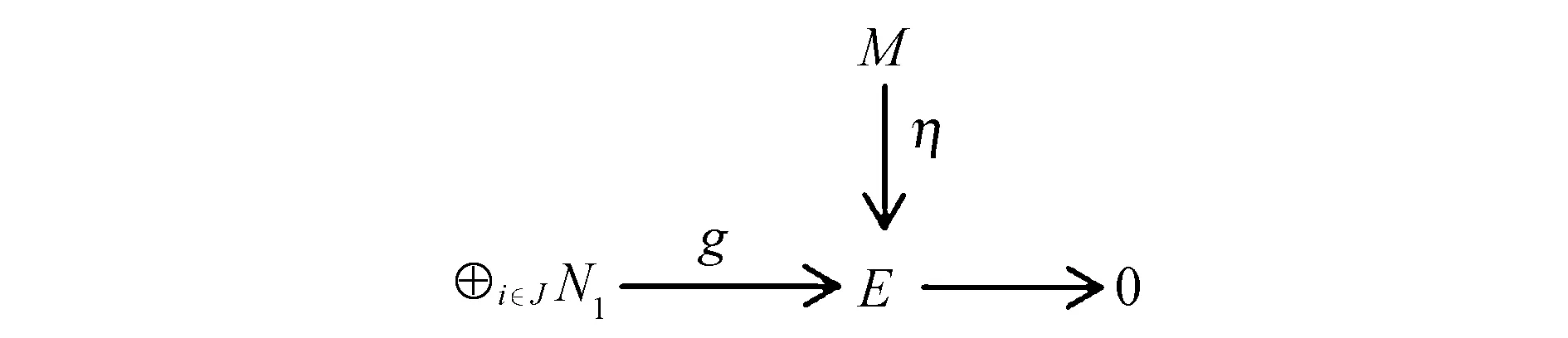
图8 交换图Fig.8 Commutative diagram

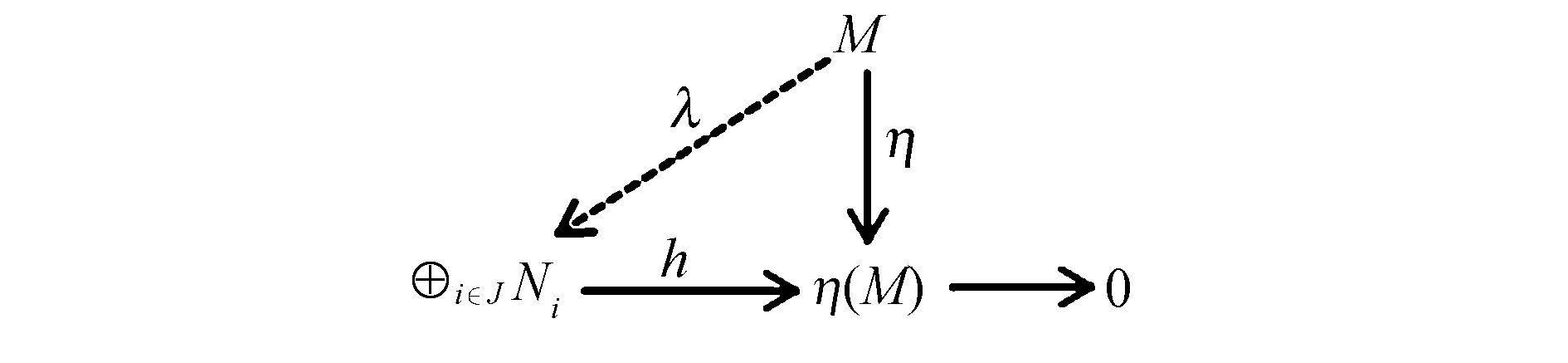
图9 交换图Fig.9 Commutative diagram
因为Fi◁Ni,M是相对于模Ni的完全不变子模Fi的Ni-投射模(i∈J)且⊕i∈JFi◁⊕i∈JNi,所以M是相对于模⊕i∈JNi的完全不变子模⊕i∈JFi的⊕i∈JNi-投射模.故存在同态λ:M→⊕i∈JNi⊆⊕i∈INi使得hλ=gλ=η.因此M是相对于模⊕i∈INi的完全不变子模⊕i∈IFi的⊕i∈INi-投射模.


定理1设N是右R-模,F◁N.则下列条件等价:
1) 每个右R-模是相对于模N的完全不变子模F的N-投射模;
2)N的每个同态像是相对于模N的完全不变子模F的N-投射模;
3)N=F⊕A,其中A是半单模;
4)N=F+Soc(N).
证明1)⟹2) 显然.
2)⟹3) 因为N/F是相对于模N的完全不变子模F的N-投射模,所以自然满同态f:N→N/F可裂,从而F≤⊕N.即存在A≤N使得N=F⊕A.设K/F◁N/F且K/F⊆H/F≤N/F.因为N/H是相对于模N的完全不变子模F的N-投射模,所以由命题2中3)可知N/H是相对于模N/F的完全不变子模K/F的N/F-投射模.故N/H是N/F-投射模,从而自然满同态g:N/F→(N/F)/(H/F)可裂,H/F≤⊕N/F.因此N/F是半单模.因为N/F≅A,所以A是半单模.
3)⟹1) 考虑图10.
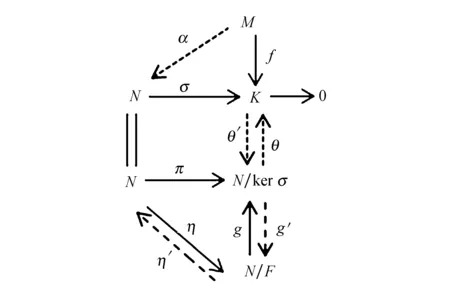
图10 交换图Fig.10 Commutative diagram
其中F⊆kerσ,π:Ν→Ν/kerσ是自然满同态.因为σ,π是满同态且kerπ=kerσ,所以由同态分解定理可知存在同构θ:N/kerσ→K使得σ=θπ.因为F⊆kerσ,所以可定义满同态g:N/F→N/kerσ,g(n+F)=n+kerσ使得π=gη,其中η:Ν→Ν/F是自然满同态.由N/F是半单模可知满同态g可裂,即存在同态g′:N/kerσ→N/F使得gg′=1N/ker σ.由假设可知F≤⊕N,故自然满同态η可裂,即存在同态η′:N/F→N使得ηη′=1N/F.因此θπη′g′θ-1f=θgηη′g′θ-1f=f.取α∶=η′g′θ-1f,θπα=σα=f,进而M是相对于模N的完全不变子模F的N-投射模.
3)⟹4) 因为N=F⊕A,其中A是半单模,所以N=F⊕Soc(A),从而N=N+Soc(N)=F⊕Soc(A)+Soc(N)=F+Soc(N).因此N=F+Soc(N).
4)⟹3) 假设N=F+Soc(N).当F∩Soc(N)=0时,结论显然成立.当F∩Soc(N)=B≠0时,B≤⊕Soc(N),故N=F+Soc(N)=F+(A⊕B)=F+A,其中A是N的半单子模.由(F∩A)∩Soc(A)⊆(F∩Soc(N))∩Soc(A)=B∩A=0可知F∩A=0.因此N=F⊕A,其中A是半单模.
推论3[9]设N是右R-模.则下列条件等价:
1) 每个右R-模是N-投射模;
2)N的每个同态像是N-投射模;
3)N是半单模.
证明在定理1中取F=0即可.
引理1[12]设M是右R-模,N≤M.则下列两条等价:
1)N≪δM.
2) 若A≤M,M=A+N,则M=A⊕B,其中B是N的投射半单子模.
定理2设N是右R-模,F◁N.若F是半单模或F≪δN,则下列条件等价:
1) 每个右R-模是相对于模N的完全不变子模F的N-投射模;
2)N的每个同态像是相对于模N的完全不变子模F的N-投射模;
3)N是半单模.
证明当F是半单模时,由定理1即证.下设F≪δN.
3)⟹1)⟹2) 显然.
2)⟹3) 由定理1可知N=F⊕A,其中A是半单模.因为F≪δN,所以由引理1可知N=B⊕A,其中B是F的投射半单子模,故N是半单模.
推论4[2]设N是有限生成右R-模.则下列条件等价:
1) 每个右R-模是Rad-N-投射模;
2)N的每个同态像是Rad-N-投射模;
3)N是半单模.
证明若N是有限生成右R-模,则
Rad(N)≪δN
故由定理2即可证得.
推论5[1]设Ν是右R-模.则下列条件等价:
1) 每个右R-模是Soc-N-投射模;
2)N的每个同态像是Soc-N-投射模;
3)N是半单模.
证明因为Soc(N)是N的半单子模,所以由定理2即可证得.
推论6设R是环.则下列条件等价:
1)R是半单环;
2) 每个右R-模是RR-投射模;
3) 每个右R-模是Rad-投射模;
4) 每个右R-模是Soc-投射模.
定理3设R是环,M是右R-模,F◁E(M).则下列条件等价:
1) 相对于模E(M)的完全不变子模F的E(M)-投射模的子模是相对于模E(M)的完全不变子模F的E(M)-投射模;
2) 投射右R-模的子模是相对于模E(M)的完全不变子模F的E(M)-投射模;
3)R的右理想是相对于模E(M)的完全不变子模F的E(M)-投射模;
4)E(M)/F的商模是内射模.
证明1)⟹2)⟹3) 显然.
3)⟹4) 设I是R的右理想,K是E(M)/F的同态像.考虑图11.
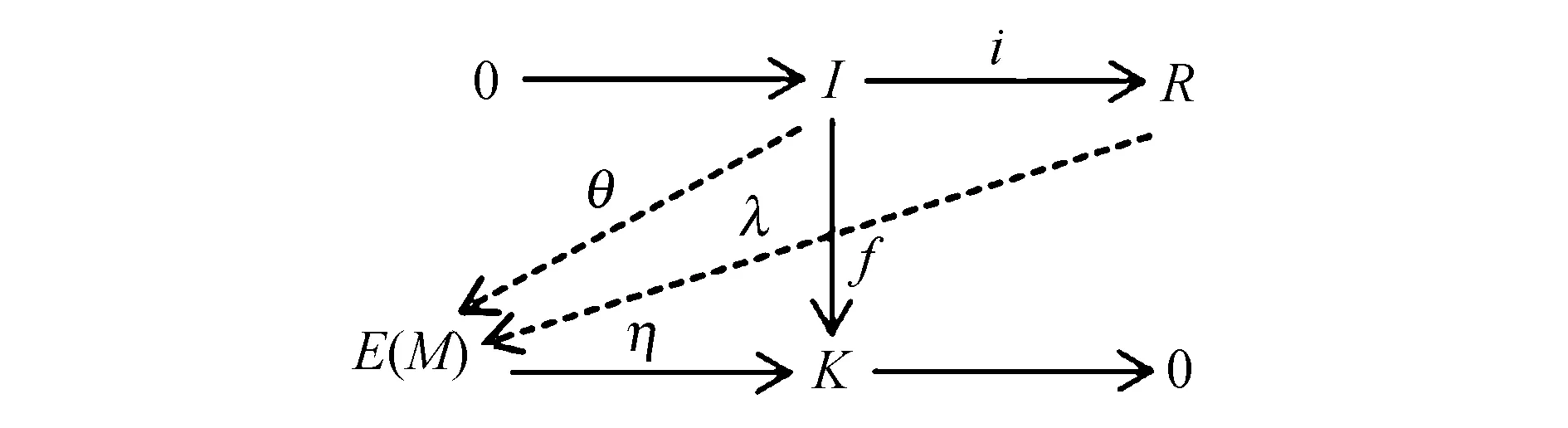
图11 交换图Fig.11 Commutative diagram
由假设可知I是相对于模E(M)的完全不变子模F的E(M)-投射模,故存在同态θ:I→E(M)使得ηθ=f.因为E(M)是内射模,所以存在同态λ:R→E(M)使得λi=θ,故ηλi=ηθ=f.设g∶=ηλ:R→Κ,则g是f的扩张.故由Bear准则可知K是内射模.
4)⟹1) 设B是相对于模E(M)的完全不变子模F的E(M)-投射模,A≤B.考虑图12.
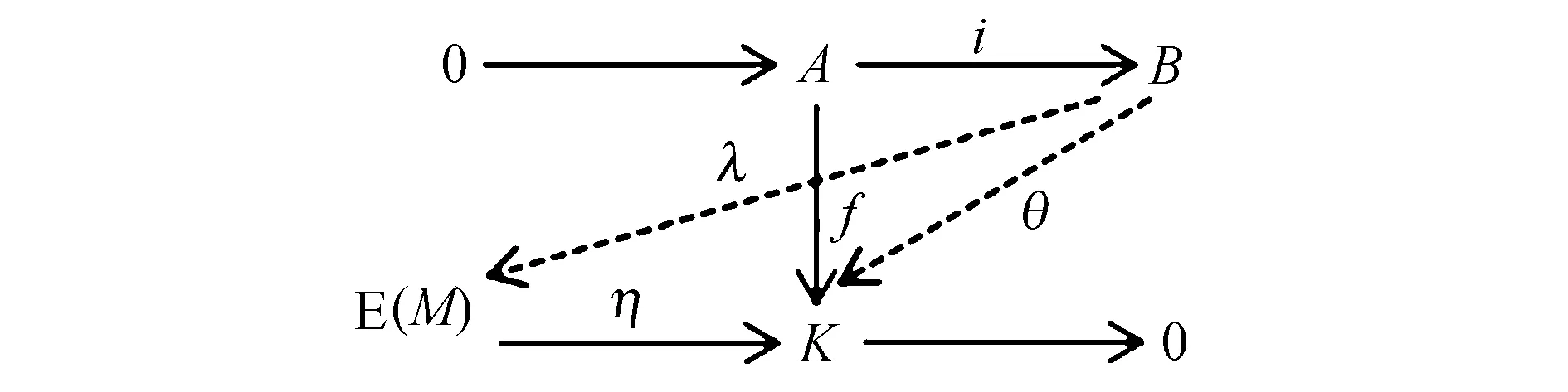
图12 交换图Fig.12 Commutative diagram
其中K是E(M)/F的同态像.因为K是内射模,所以f可以扩张到同态θ:B→K使得f=θi.因为B是相对于模E(M)的完全不变子模F的E(M)-投射模,所以存在同态λ:B→E(M)使得ηλ=θ.由ηλi(x)=ηλ(x)=θ(x)=f(x),x∈A可知同态λi:A→E(M)是f的提升,故A是相对于模E(M)的完全不变子模F的E(M)-投射模.
推论7设M是右R-模.则下列条件等价:
1) E(M)-投射模的子模是E(M)-投射模;
2) 投射右R-模的子模是E(M)-投射模;
3)R的右理想E(M)-投射模;
4) E(M)的商模是内射模.
证明在定理3中取F=0即可.
推论8设M是内射右R-模,F◁M.则下列条件等价:
1) 相对于模M的完全不变子模F的M-投射模的子模是相对于模M的完全不变子模F的M-投射模;
2) 投射右R-模的子模是相对于模M的完全不变子模F的M-投射模;
3)R的右理想是相对于模M的完全不变子模F的M-投射模;
4)M/F的商模是内射模.
证明若M是内射右R-模,则M=E(M),故由定理3即可证得.
推论9设R是环,M是内射右R-模.则下列条件等价:
1)R是右遗传环;
2)M-投射模的子模是M-投射模;
3) 投射右R-模的子模是M-投射模;
4)R的右理想是M-投射模.
证明在推论8中取F=0即可证得.
命题4设M和N是右R-模,F◁N.若N/F是半单模,则下列两条等价:
1)M是相对于模N的完全不变子模F的N-投射模.
2) 每个同态γ:M→N/F可以被提升到同态λ:M→N使得γ=ηλ,其中η:N→N/F是自然满同态.
证明1)⟹2) 显然.
2)⟹1) 考虑图13.
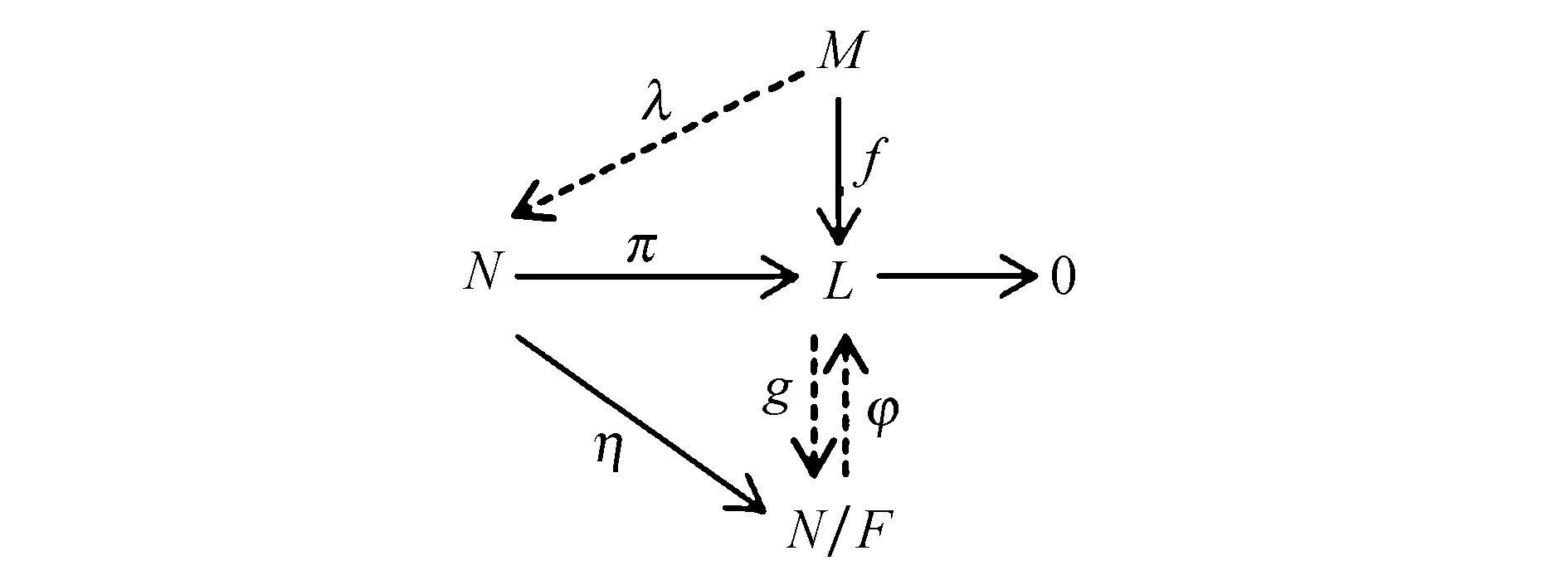
图13 交换图Fig.13 Commutative diagram
其中F⊆kerπ.因为η,π是满同态且F=kerη⊆kerπ,所以由同态分解定理可知存在满同态φ:N/F→L使得π=φη.因为N/F是半单模所以满同态φ可裂,即存在同态g:L→N/F使得φg=1L.由假设可知存在同态λ:M→N使得ηλ=gf.因此πλ=φηλ=φgf=1Lf=f,故λ为所求同态,即M是相对于模N的完全不变子模F的N-投射模.
命题5设N1,N2是右R-模,F1⊕F2◁N1⊕N2,其中F1≤N1,F2≤N2.若N1⊕N2是相对于模N1⊕N2的完全不变子模F1⊕F2的N1⊕N2-投射模,则每个满同态f:N1→N2可裂,其中F1⊆kerf.另外,若N1是投射模,则N2是投射模.
证明设f:N1→N2是满同态且F1⊆kerf.考虑图14.
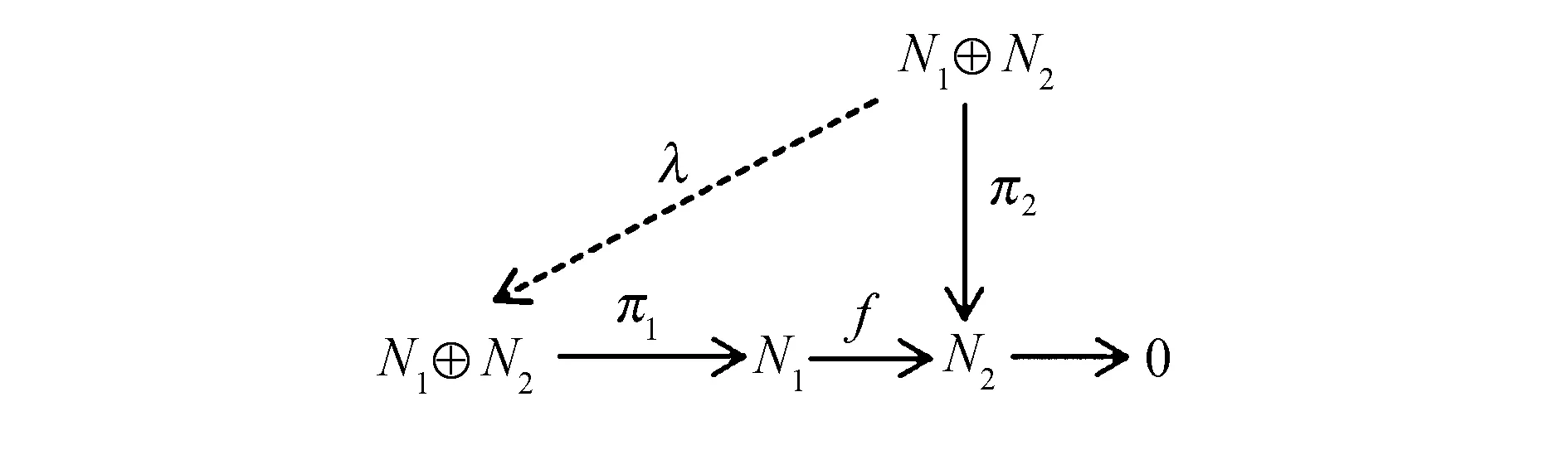
图14 交换图Fig.14 Commutative diagram

定义2设M是右R-模,I◁RR.称M是相对于理想I的R-投射模,若M是相对于模RR的完全不变子模I的RR-投射模.
注2设R是环,I◁RR.当I=0时,相对于理想I的R-投射模是R-投射模;当I=τ(R)时,相对于理想I的R-投射模是τ-投射模;当I=Rad(R)时,相对于理想I的R-投射模是Rad-投射模;当I=R时,每个右R-模都是相对于理想I的R-投射模.

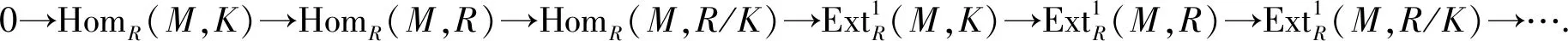
定理4设R是环,I◁RR.若I≪δRR,则R是半单环当且仅当R/I是半单的且是相对于理想I的R-投射模.
证明“⟹”因为R是半单环,所以R/I是半单的且每个右R-模是投射的,故R/I是相对于理想I的R-投射模.
“⟸” 因为R/I是相对于理想I的R-投射模,所以满同态R→R/I可裂,从而I≤⊕R,即存在R的右理想T使得R=I⊕T,故R/I≅T,进而由R/I是半单的可知T是半单模.因为I≪δRR,所以由引理1可知R=Y⊕T,其中Y是I的半单投射右理想.因此R是半单环.
命题7设R是环,M是右R-模,I◁RR.若I⊆δ(R)且M是相对于理想I的R-投射模,则下列条件等价:
1)M是生成子;
2)M生成每个单右R-模;
3) 对任意单右R-模S,Hom(M,S)≠0.
证明1)⟹2)⟹3) 显然.
3)⟹1) 假设TR(M)≠R.故TR(M)⊆A,其中A是R的极大理想.因为R/A是单模,所以由前提条件可知存在非零同态f:M→R/A.考虑图15.
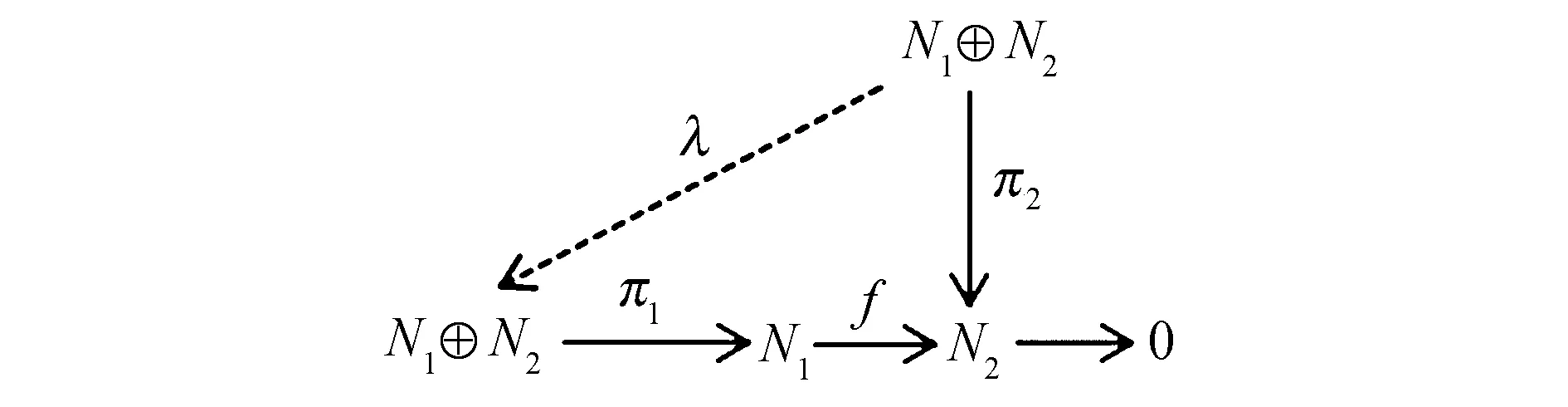
图15 交换图Fig.15 Commutative diagram
其中η:R→R/A是自然满同态.若R/A是奇异模,则η(I)⊆η(δ(R))⊆δ(R/A)=0,故I⊆kerη.由M是相对于理想I的R-投射模可知存在同态λ:M→R使得图15可换.若R/A是投射模,则满同态η可裂,存在同态λ:M→R使得图15可换.故上述两种情况都存在同态λ使得ηλ=f.由Imλ⊆TR(M)⊆A=kerη可知f=ηλ=0,矛盾.因此TR(M)=R,M是生成子.
定理5设R是环,I◁RR.若I⊆δ(R),则下列条件等价:
1)R是GV-环;
2) 每个右R-模的小子模是投射模;
3) 每个右R-模的小子模是相对于理想I的R-投射模;
4) 每个小右R-模是相对于理想I的R-投射模.
证明1)⟹2) 设M是右R-模,K≪M.当K=0时,显然成立.当0≠x∈K时,令A是xR的极大子模.若xR/A是奇异模,则由假设可知xR/A是内射模,故xR/A≤⊕M/A.因为A≤xR≤K≪M,所以A≤xR≪M,故xR/A≪M/A,从而xR/A=0,矛盾.因此xR/A不是奇异模,而是投射模,故A≤⊕xR,从而xR和K是半单模.令K=⊕i∈IKi,其中Ki是K的单子模.若Ki是奇异模,则由假设可知Ki是内射模,故Ki≤⊕M.因为Ki≤K≪M,以Ki≪M,故Ki=0,矛盾.因此Ki不是奇异模,而是投射模,故K是投射模.
2)⟹3)⟹4) 显然.
4)⟹1) 设M是奇异单右R-模.若M≪E(M),则由假设可知M是相对于理想I的R-投射模.考虑图16.
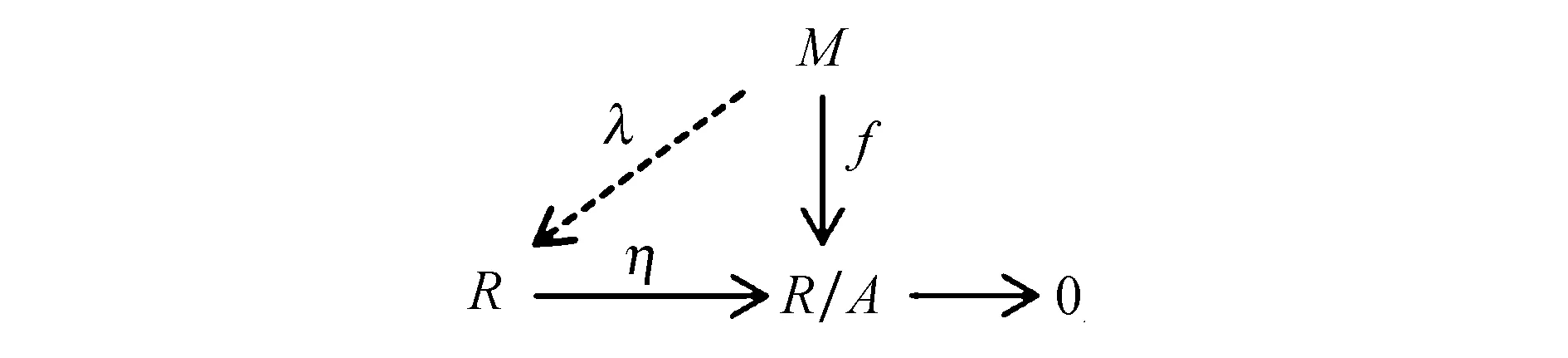
图16 交换图Fig.16 Commutative diagram
对任意g:R→M的满同态有g(I)⊆g(δ(R))⊆δ(M)=0可知I⊆kerg.因为M是相对于理想I的R-投射模,所以存在同态h:M→R使得gh=id,故满同态g可裂,从而M是投射模,矛盾.因此M不是E(M)的小子模,故存在E(M)的真子模K使得E(M)=K+M.因为K∩M=0,所以M≤⊕E(M).因此M是内射模.
推论10[2]设R是环.则下列条件等价:
1)R是GV-环;
2) 每个右R-模的小子模是投射模;
3) 每个右R-模的小子模是Rad-投射模;
4) 每个小右R-模是Rad-投射模.
证明因为Rad(R)⊆δ(R),所以由定理5即可证得.

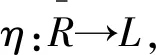

图17 交换图Fig.17 Commutative diagram
命题9设R是环,I◁RR.若I⊆δ(R),则每个单相对于理想I的R-投射模是投射的.
证明设S是单相对于理想I的R-投射模.若S是奇异模,η:R→S是自然满同态,则η(I)⊆η(δ(R))⊆δ(S)=0,即I⊆kerη.因为S是相对于理想I的R-投射模,所以满同态η可裂,故S是投射模,矛盾.因此S不是奇异模而是投射模.
