(喀什大学数学与统计学院，新疆喀什 844000)

算术基本定理或唯一因子分解定理指出：每个大于1 的整数均可以唯一地表示成一些素数幂的乘积.下文均称唯一因子分解定理.这个重要定理有多种证明方法和应用[1-3].在初等数论中，用于研究Riemann-zeta 函数就是其最重要的应用.

设s∈C 且Re s＞1，则Riemann-zeta 函数由

所定义.当你第一次看到这个函数时，根本不清楚为什么它值得研究，或者为什么凯莱数学研究所提供100 万美元用于资助研究其零点的位置问题！事实证明，Riemann-zeta 函数是数论中最重要的函数之一.由唯一因子分解定理，可将 Riemann-zeta 函数重新改写为乘积形式，即若Re s＞1，则

其中P 是素数的集合[4].Riemann-zeta 函数的这种关系是许多数论问题研究的出发点.虽然整数可表为素数的乘积，但是要准确掌握素数的分布和性质却是十分困难的[5].相反，整数就很好理解.比如，素数17483 之后的下一个素数是什么?（是17489）并不是显而易见的；但是，我们却很容易找到17483 之后的下一个整数！然而，由于和与积是等价的，所以我们可将整数的信息转换为素数的信息，而解决问题的关键在于证明唯一因子分解定理.

本文的目的不只是为了讨论唯一因子分解定理或类似结果的证明，而是要强调在试图证明某个命题时，如何巧妙地应用假设所蕴含的事实.

定理1（唯一因子分解定理）每个大于1 的正整数均可以唯一地表示成一些素数幂的乘积.

分析：证明要分两个步骤.

（1）证明每个整数至少可写为两种素数幂的乘积，即存在性；

（2）证明这两种分解（需重新排列因子顺序）是相同的，即唯一性.

众所周知，整数n≥2 称为素数，如果它只能被1 和自身整除，1 称为单位.非素数的其它正整数称为合数.这里要注意，1是单位而非素数，否则唯一因子分解定理不 成立.例 如，6=1·2·3=12020·2·3.这就是为什么在素数定义中要求整数必须大于等于2 的原因.

第二数学归纳法是证明唯一因子分解定理存在性的一种有效方法，它与第一数学归纳法类似.两者都要求证明命题P（n）n 对n=1(或另一个固定的自然数r，这取决于命题的起始计数）正确.在第一数学归纳法中，需证明：若P（n）正确，则P（n+1）也正确，并得出P（n）对所有n≥r 正确的结论；在第二数学归纳法中，需证明：若P（k）对所有k≤n 正确，则P （n+1）也正确，并得出P（n）对所有n≥r 正确的结论.

证明：（1）存在性.显然，2 是素数幂的乘积，因为2 本身就是素数.假设所有正整数k（2≤k≤n）均可写成素数幂的乘积.现在，考虑正整数n+1.它或者是素数（证明完成），或者可被某个素数p 整除，即p|（n+1）(因为若n+1 不是素数，则它为合数.于是，n+1 可分解成两个小于n 的正整数乘积.如此下去，便可找到素数p.）.令n+1=pm，其中m＜n，由假设，m 可表为素数幂的乘积.因此，由第二数学归纳法，存在性得证.

为了证明唯一性，先给出下面引理.

引理1给定素数p 和整数a，b.若p|ab，则p|a 或p|b.

我们把引理1 的证明放到最后.这里需要强调的是，引理1 是证明定理1 唯一性的关键，即一旦证明了引理1，唯一性证明的剩余部分随即可得.

（2）唯一性.用反证法.若因子分解的唯一性不成立，则必有一个最小正整数，设为n，其因子分解的唯一性不成立.因此，不妨设n 有两个不同的因子分解式，即

现在，考察n／pk＜n.显然，它只有唯一的因子分解式.否则，将与n 是具有两个不同因子分解式的最小整数的假设矛盾.

定理1 证毕.

由此可见，整数环上因子分解的唯一性，关键是要证明引理1 正确.这一点尽管看起来很简单，但必须得到严格证明，尤其是在某些环上，归纳法失效的情况下更是如此! 例如，考虑高斯环

的函数构成的环，其中ai，bi∈R 且n∈N .在这里，由于

所以，三角多项式环上因子分解的唯一性不成立[6]，并且sinx 既不整除1-cosx，也不整除1+cosx.

关于引理1 的证明，许多教材使用的标准方法都是Euclidean 算法（带余除法）或贝祖等式[3].

所谓贝祖等式，即下面的定理.

定理2（贝祖等式）给定a，b∈Z，∃x，y∈Z，使得xa+yb=gcd （a，b）(其中gcd （a，b）是a 和b 的最大公因数），即同时整除a 和b 的最大整数.

证明 只证明gcd （a，b）=1 的情况，当gcd（a，b）=d＞1 的情况类似可证.在这里，给出x 和y存在性的一个新的非构造性证明.设

为了完成证明，必须推出k=1.首先，证明k整除A 中的每一个数.假设情况并非如此，即k 不能整除A 中的每一个数.由于这个数在A 中，所以必有整数x1和y1，使得它等于x1a +y1b.设n 是满足nk＜x1a +y1b＜（n+1）k 的最大自然数.因为，我们一直在增加k 的倍数，直到它首次超过x1a+y1b为止.而且，必须有

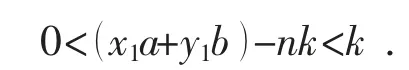
不妨设在第q 步时，中间表达式等于0，于是x1a+y1b=qk，即k| （x1a+y1b）.这与x1a+y1b 是A 中不能被最小数k 整除的假设矛盾.类似地，可以证明中间表达式也不能等于k.

因为k=x0a+y0b，所以有

由于这是一个正数且形如xa+yb，因此它必属于A.此外，它严格小于k，这与k 是A 的最小数矛盾.因此，A 中存在一个不能被k 整除的数的假设错误，从而A 中的所有数都可被k 整除.

特别地，若取x=1，y=0，则a∈A；同时，若x=0，y=1，则b∈A.因此，k|a 且k|b .因为gcd（a，b）=1，即a 和b 没有公因数，所以必有k=1.因此，适当选取x0和y0，可得1=x0a+y0b.

定理2 证毕.

贝祖等式对引理1 的证明至关重要.事实上，假设p|ab，但.将贝祖等式应用于p 和a 上.注意到，gcd（p，a）=1.因此，∃x，y∈¢，使得xp+ya=1.两边乘以b，可得xpb+yab=b.因p|p且p|ab，故p|（xpb+yab），即p|b.矛盾！可见，贝祖等式起到了“桥”的作用.

注1：贝祖等式的逆命题不成立！

在使用贝祖等式时，认为没有k|gcd（a，b），就能有k|a 和k|b 是非常错误的.幸运地是，在因子分解唯一环中，证明k|gcd（a，b）却相当简单!

引理2在因子分解唯一环Z 中，给定a，b∈Z 和k∈N .若k|a 且k|b，则k|gcd（a，b）.

证明 由唯一因子分解定理，可设a 和b 可以分别表示为

其中ri，si∈N （i=1，…，l）.令可以证明d=gcd （a，b），此处省略.

若k|a 且k|b，则k 可写为

注意到，由k|a，可得ui≤ri（i=1，…，l）.同样，由k|b，可得ui≤si（i=1，…，l）.于是，有ui≤min(ri，si)=ti（i=1，…，l）.因此，可得k|d.

引理2 证毕.

注2：从引理2 的证明过程可以发现唯一因子分解定理的另一个应用，即寻找两个整数的最大公因数.

现在，回到证明引理1 的问题上.顺便说一句，为了证明唯一因子分解定理，只需引理1 就够了，而不需要有比贝祖等式更强的命题了.下面，给出引理1 的强调两种不同观点的证明.这两种证明都用到了Euclidean 算法（带余除法），即设a，p∈N.若a＞p 且则∃n∈N 和r∈{1，…，p-1}，使得a=np+r.值得注意的是，引理1 的两种证明都未使用有关最大公因数（在Euclidean算法的标准证明中用到）的任何结果，但却用到了最小数原理，即具有某种性质的任何非空正整数集必有一个最小数.

引理1证法一：

由前面的讨论已知，若p为素数且gcd（a，p）=1，则∃x，y∈Z，使得xp+ya=1.然后，两边同乘以b，得到xpb+yab=b.若假设则由已知条件和整除的性质可知p|（xpb+yab），从而p|b.

引理1证法二：

（2）假设这样的素数p 存在，a 和b 使得乘积ab 在所有整数乘积中最小.若分解a 和b 之后，有几个乘积都得到相同的最小乘积，为明确起见，则取包含a 的那个最小乘积.

（3）证明a，b＜p.显然，a，b≠p.假设a＞p（b＞p时同样）.由带余除法定理，a 可写为a=np+r 且0＜r＜p.于是，ab=（np+r）b=nbp+rb.因p|ab，故p|rb.然而，rb＜ab，这与乘积ab 的最小性矛盾.因此，有a，b＜p.

（4）由于所有整数都有素因数分解，所以可将ab 写为ab=qa，1…qa，l·qb，l…qb，m.根据p|ab 的假设，可将ab 改写为ab=np （n∈N） .因此，有np=qa，1…qa，l·qb，l…qb，m.

由假设（1），存在一个乘积，使得p 为整除该乘积，但不整除两个因数的最小素数.由于a 的因数最多只有a＜p 个（b 的因数最多只有b＜p个），所以由归纳法可得，每个因数qa，i和qb，j，或者整除n，或者整除p.因p 是素数，故qa，1，…qb，m均不能整除p，又因为已假设如果qa，1|p，那么就有qa，1=p .从而，p|a.矛盾！

（5）由于每个因数qa，1，…，qb，m均整除n，所以当ab=np 时，可得这是不可能的，因为p≥2.

综上可知，不可能存在这样一个最小素数，它整除乘积，但不整除乘积中的任何一个因数.

引理1 证毕.

素数整除一个乘积就必须整除其中的某个因数.这个结论是证明唯一因子分解定理的关键所在.本文实现了两个目的.一是强调了那些看似平常的陈述必须严格证明.因为学生很容易被符号所误导.例如，两个整数的最大公因数实际上就是它们公因数中最大的那个.但在具体问题的证明中，学生往往忽视对“公共”这一点的证明；二是要准确、全面地把握住结论的内涵，具体地说，就是要证明某个结论成立，究竟需要多少论据来支撑这些逻辑推理.