一、选择题

1.B

2.B

3.C

4.D 提示:如图1,由两个结构相同的三棱锥叠放在一起构成的几何体,各面都是三角形,但它不是棱锥,A错误。如图2,若△ABC不是直角三角形,或是直角三角形但旋转轴不是直角边,所得的几何体都不是圆锥,B错误。

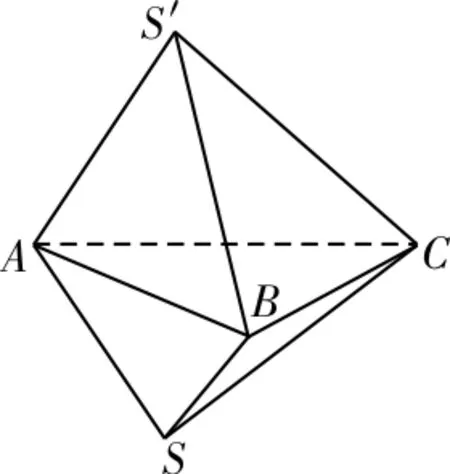
图1

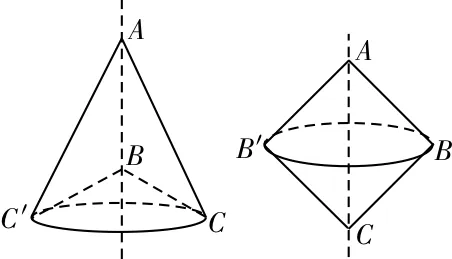
图2

若六棱锥的所有棱都相等,则底面多边形是正六边形。但由几何图形知,若以正六边形为底面,侧棱长必然要大于底面边长,C错误。

5.B

6.A

7.D 提示:因为AD与PB在底面内的射影AB不垂直,所以PB⊥AD不成立；又平面PAB⊥平面PAE,所以平面PAB⊥平面PBC也不成立；BC∥AD,AD⊂平面PAD,所以BC∥平面PAD,而平面PAD与平面PAE相交,所以直线BC∥平面PAE也不成立；在Rt△PAD中,PA=AD=2AB,所以∠PDA=45°。

8.C 提示:设球心为Oˊ,如图3所示,则OˊO=2,由正弦定理得,2|OC|2,|OC|=1。球半径R=OOˊ2+OC2=,所以S球=4πR2=20π。

9.B 提示:从所给的三视图可以得到该几何体为三棱锥,本题所求表面积为三棱锥四个面的面积之和,图4为其直观图,由三视图知其相关数据。利用垂直关系和三角形面×6=65,因此该几何体的表面积为S=30+65。

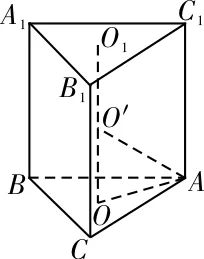
图3

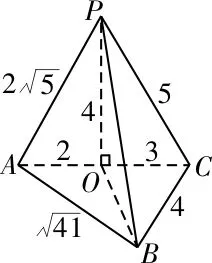
图4

10.B

11.D

12.A

13.C 提示:如图5所示,平行六面体ABCDA1B1C1D1中与AB,CC1都共面的棱为BC,C1D1,DC,AA1,BB1,共5条。

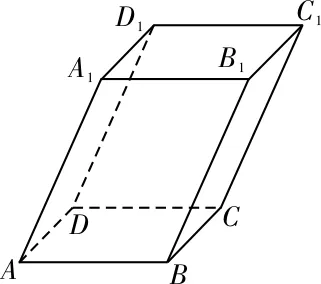
图5

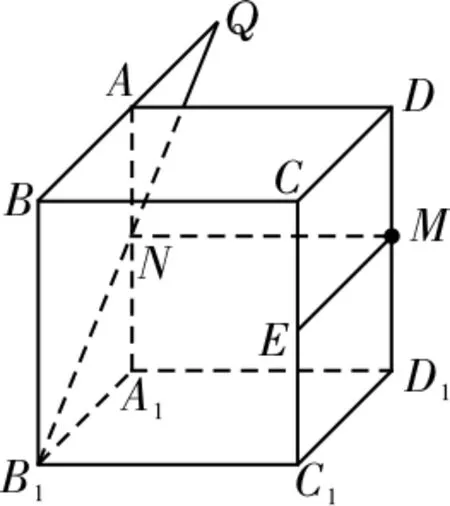
图6

14.C 提示:如图6所示,因为点M不在B1C1上,所以由B1C1与点M可确定唯一平面B1C1M。设此平面与AA1的交点为N,则N为AA1的中点。在平面ABB1A1内,B1N与BA必相交,设交点为Q,则QM与B1C1一定不平行,所以QM与AB,B1C1都相交。由作法知,这样的直线QM有且仅有一条,所以①真。因为AB∥A1B1,A1B1与B1C1相交确定一个平面A1B1C1D1,因为过点M作平面A1B1C1D1的垂线唯一,所以过点M与AB,B1C1都垂直的直线唯一,所以②真。过点M作ME∥DC,交CC1于点E,因为DC∥AB,所以ME∥AB,过点M作MF∥A1D1,交AA1于点F,因为A1D1∥B1C1,所以 MF∥B1C1,所以AB 与B1C1都与平面MEF平行,由作法知,这样的平面MEF有且仅有一个,所以④真。

图7

16.B

17.D 提示:以A为原点,AB,AD,AA1所在直线为x轴,y轴,z轴,建立如图8所示的空间直角坐标系。设AB=1,则A(0,0,0),B(1,0,0),A1(0,0,2),D1(0,1,2),所(0,1,2)。因为面直线A1B与AD1所成角的余弦值为

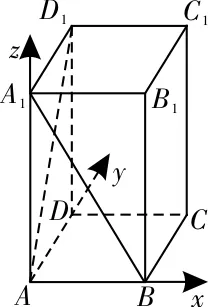
图8

18.A 提示:由条件知AC,BC,CC1两两垂直,以C为原点,CB,CA,CC1分别为x轴,y轴,z轴,建立空间直角坐标系,如图9所示,则B(1,0,0),A(0,3,0),B1(1,0,

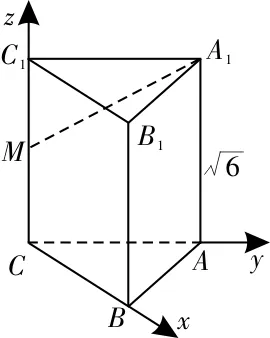
图9

19.B 提示:过球心O向棱l作垂面MNP,截面如图10所示,由圆的性质知MQ⊥OP,OM⊥MP,MQ==2,Rt△MQOr2=1,球O的表面积为S=4πr2=4π。

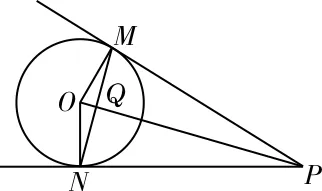
图10

20.D

21.B 提示:设该四面体为S-ABC,D为AC边的中点,如图11。

(1)当SA=SC=AB=BC=1,AC=2,平面SAC⊥平面ABC时,VS-ABC最大,此

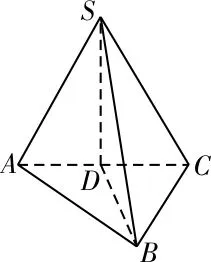
图11

(2)当AB=BC=CA=SA=1,SC=2,平面SAC⊥平面ABC时,VS-ABC最大,此,故此时满足的四面体有2个,这两个四面体中SB=3或1。

综合(1)(2)知满足题意的四面体有3个。

22.C

23.B

24.B 提示:如图12所示,以正方形ABCD的中心O为原点,与边BC,CD垂直的直线分别为x轴,y轴,OP为z轴,建立空间直角坐标系。由条件知C(1,1,0),D(-1,1,0),P(0,0,3),所以设n=(x,y,z),则n·=0,所以x+y=0,-x=0,所以x=y=0,取n=(0,0,1)。 又所以

图12

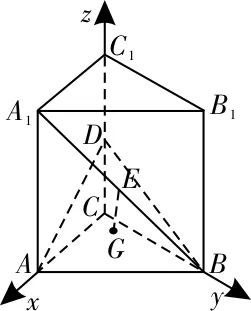
图13

25.B 提示:以C为坐标原点,CA,CB,CC1所在直线为x轴,y轴,z轴,建立如图13所示的空间直角坐标系。设CA=CB=a,则A(a,0,0),B(0,a,0),A1(a,0,2),D(0,0,1),所以=(0,-a,1)。因为点E在平面ABD上的射影是△ABD的重心G,所以平面 ABD,所以=0,(2,-2,2)。因为平 面 ABD,所以为平面ABD的一个法向量。因为cos〈以A1B与平面ABD所成的角的余弦值为

26.C

27.C

28.C

二、填空题

30.9 提示:如图14所示,设圆台的母线长为l,则由相似,得l=9(cm)。

图14

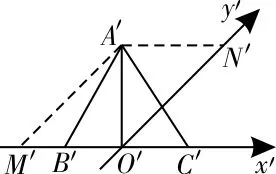
图15

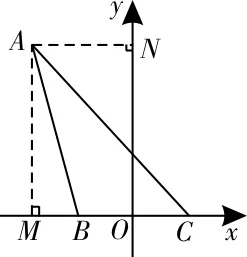
图16

图17

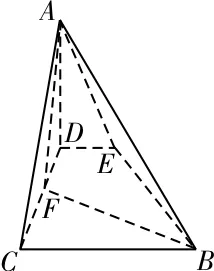
图18

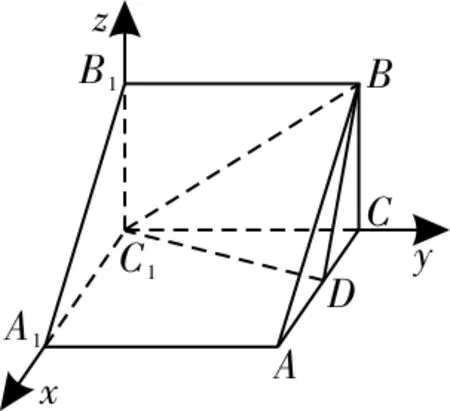
图19

36.6 提示:如图20,过点Cˊ作CˊD∥AˊBˊ,交yˊ轴于点D,作CˊE∥yˊ轴,交xˊ轴于点E。因为正△ABC的边长为2,所以DCˊ=AˊE=EBˊ=1,DAˊ=CˊE=。因为∠AˊDCˊ=135°,所以CˊAˊ2=DAˊ2+CˊD2-2DAˊ·CˊD·cos135°=45°),所以CˊAˊ2-CˊBˊ2=6。

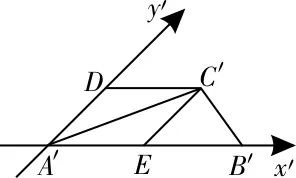
图20

37.4

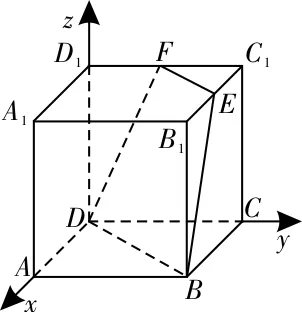
图21

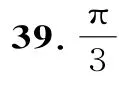
40.2+22 提示:由题意知,正视图就是如图22所示的截面PEF,其中E,F分别是AD,BC的中点,连接AO,易得AO=2,而PA=3,于是解得PO=1,所以PE=2,故其正视图的周长为2+22。

图22

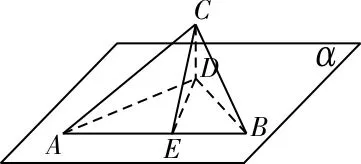
图23

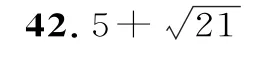
图24

设面AEC1F的法向量为n=(1,λ,μ),则有n·=0,n·=0。

三、解答题

44.(1)如图25所示,取BD的中点M,连接MC,FM。

因为F为BD1的中点,所

图25

又CM⊥平面DBD1,所以EF⊥平面DBD1。因为BD1⊂面DBD1,所以EF⊥BD1,故EF为BD1和CC1的公垂线。

(2)连接ED1,有VE-DBD1=VD1-DBE,由(1)知EF⊥平面DBD1,设点D1到平面BDE的距离为d,则S△DBE·d=S△DBD1·EF。因为AA1=2,AB=1,所以BD=BE=ED=,故点D1到平面DBE的距离

45.存在点E,且E为AB的中点。

下面给出证明:

如图26所示,取BB1的中点F,连接DF,则DF∥B1C1。因为AB的中点为E,连接EF,则EF∥AB1。因为B1C1与AB1是相交直线,所以平面DEF∥平面AB1C1。而DE⊂平面DEF,所以DE∥平面AB1C1。

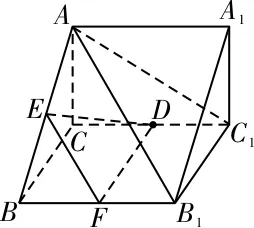
图26

46.(1)如图27所示,取BC的中点G,连接AG,EG,因为E是B1C的中点,所以

图27

由直棱柱知,AA1∥BB1,而D是AA1的中点,所以EGAD,所以四边形EGAD是平行四边形,所以ED∥AG。又DE⊄平面ABC,AG⊂平面ABC,所以DE∥平面ABC。

(2)因为AD∥BB1,所以AD∥平面BCE,所以VE-BCD=VD-BCE=VA-BCE=VE-ABC,由(1)知,DE∥平面ABC,所以VE-ABC=4=12。

47.(1)由题意可知,在四棱锥B-ACDE中,平面ABC⊥平面ACDE,AB⊥AC,所以AB⊥平面ACDE。

又AC=AB=AE=2,DE=4,则四棱锥B-ACDE的体积为

(3)因为AC=AB,N是BC的中点,所以AN⊥BC。在直三棱柱中,平面ABC⊥平面BCD,所以AN⊥平面BCD。由(2)知AN∥EM,EM⊥平面BCD,又EM⊂平面BDE,所以平面BDE⊥平面BCD。

48.(1)当E为BC的中点时,EF与平面PAC平行。

在△PBC中,E,F分别为BC,PB的中点,所以EF∥PC。又EF⊄平面PAC,而PC⊂平面PAC,所以EF∥平面PAC。

(2)因为PA⊥平面ABCD,BE⊂平面ABCD,所以EB⊥PA。又EB⊥AB,AB∩AP=A,AB,AP⊂平面PAB,所以EB⊥平面PAB。又AF⊂平面PAB,所以AF⊥BE。又PA=PB=1,F是PB的中点,所以AF⊥PB。又因为PB∩BE=B,PB,BE⊂PBE,所以AF⊥平面PBE。因为PE⊂平面PBE,所以AF⊥PE。

(3)过点A作AG⊥DE于点G,连接PG,因为DE⊥PA,则DE⊥平面PAG,故∠PGA是二面角P-DE-A的二面角,所以∠PGA=45°。

因为PD与平面ABCD所成角是30°,所以∠PDA=30°,所以 AD=3,PA=AB=1。所以AG=1,DG=2。

设BE=x,则CE=3-x。

在Rt△DCE中,(2+x)2=(3-x)2+12,得BE=x=3-2。

图28

又因为PD∥A1A,所以,所 以 ∠PED=60°,即 二 面 角P-AC-B的大小为60°。

50.(1)因为∠A1C1B1=∠ACB=90°,所以B1C1⊥CC1,所以B1C1⊥平面ACC1,所以B1C1⊥CD。由D为AA1的中点可知,DC=DC1=2,所以DC2+即CD⊥DC1。所以CD⊥平面B1C1D。又CD⊂平面B1C1D,所以平面B1CD⊥平面B1C1D。

(2)由(1)可知B1C1⊥平面ACC1A1,在平面ACC1A1内过点C1作C1E⊥CD,交CD或其延长线于点E,连接EB1,由三垂线定理可知∠B1EC1为二面角B1-DC-C1的平面角。

所以∠B1EC1=60°,由B1C1=2可知。因为△DC1C的面积为1,所以=1,解得x=2。

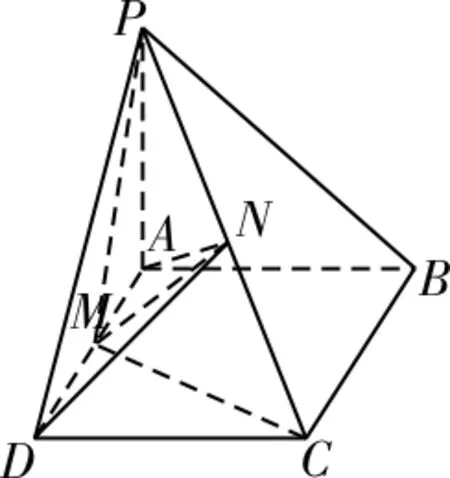
图29

51.(1)如图29所示,连接AC,AN,BN。因为PA⊥平面ABCD,所以PA⊥AC。在Rt△PAC中,N为PC的中点,所以AN=PC。因为PA⊥平面ABCD,所以PA⊥BC。又BC⊥AB,PA∩AB=A,所以BC⊥平面PAB,所以BC⊥PB。从而在Rt△PBC中,BN为斜边PC上的中线,所以BN=PC,所以AN=BN,所以△ABN为等腰三角形。又M为底边AB的中点,所以MN⊥AB。又因为AB∥CD,所以MN⊥CD。

(2)如图29所示,连接PM,CM,因为∠PDA=45°,PA⊥AD,所以AP=AD。因为四边形ABCD是矩形,所以AD=BC,所以PA=BC。又因为M为AB的中点,所以AM=BM,而∠PAM=∠CBM=90°,所以PM=CM。又因为N为PC的中点,所以MN⊥PC。由(1)知,MN⊥CD,PC∩CD=C,所以MN⊥平面PCD。

52.(1)如图30所示,连接BM,DM。在等腰梯形ABCD中,因为AD∥BC,AB=AD,∠ABC=60°,E 是BC的中点,所以△ABE与△ADE都是等边三角形,所以BM⊥AE,DM⊥AE。又BM∩DM=M,所以AE⊥平面BDM。因为BD⊂平面BDM,所以AE⊥BD。

(2)连接CM交EF于点N,连接PN。因为ME∥FC,且ME=FC,所以四边形MECF是平行四边形,所以N是线段CM的中点。因为P是线段BC的中点,所以PN∥BM。由题意可知,BM⊥平面AECD,所以PN⊥平面AECD。因为PN⊂平面PEF,所以平面PEF⊥平面AECD。

(3)由(2)可得,PN为三棱锥P-CDE的高,因为AB=2,所以BM=3,所以

图30

53.(1)如图31所示,连接A1B,AB1,交于点E,则E为A1B的中点,因为D为A1C1的中点,所以DE为△A1BC1的中位线,所以B1C∥DE。又DE⊂平面AB1D,BC1⊄平面AB1D,所以BC1∥平面AB1D。

图31

(2)过点D作DF⊥A1B1于点F,由正三棱柱的性质可知,DF⊥平面ABB1A1,AB1⊂平面ABB1A1,故DF⊥AB1,连接EF,DE,在等边三角形A1B1C1中,B1D=a,在 Rt△AA1D 中,AD=a,所以AD=B1D,所以DE⊥AB1。又DE∩DF=D,所以AB1⊥平面DFE。又FE⊂平面DFE,故EF⊥AB1,则∠DEF为二面角A1-AB1-D的平面角。又,因为△B1FE∽,故所求二面角A1-AB1-D的大小为