广州市从化区鳌头中学(510940) 薛喜双

谈谈解题后的再反思

广州市从化区鳌头中学(510940) 薛喜双

数学教学是以解题为中心展开的,要培养和提高学生的解题能力,除了做好审清题意、制定解题计划、实施解题方案等工作之外,解题后的再反思也是一个不可缺少的重要环节.

所谓解题后的再反思是指在解决了数学问题后,通过从问题特征、解题思路、解题途径、解题过程、题目结论等方面进行反思以进一步摸清数学解题所经历的前因后果的思维过程.如果学生在每一次解题以后都能对自己的解题思路、过程、策略总结归纳作自我评价,探讨成功的经验和失败的教训,对解题过程中反映的数学思想、方法进行总结、概括,就一定能达到提高解题能力和优化思维品质的目的.

下面是笔者在教学过程中引导学生进行反思的几点具体做法.

一、反思错误原因,及时反馈纠正

学生在学习基础知识时,不求甚解,满足于一知半解,加之做作业时粗心大意,考虑问题不全面,这是造成错误的主要原因;比如,在求几何线段的最大最小值问题中,在没有理解点的运动本质的前提下,随意利用三角形边长和差定理,就比较容易出错.如下例:

例一如图1,Rt△ACB中,∠ACB=90°,AC= 8,BC=6,E是斜边上的一个动点,BD⊥BC于B,F为BD上的一个动点,当AE=BF时,求CE+CF的最小值.

图1

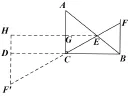
图2

分析与解:如图2,作点F′与F关于点C对称,连接EF′,显然有CE+CF′≥EF′,所以当C、E、F′共线时,CE+CF′=EF′最小,此时,BC=CD=6,AB=10,设AE=BF=x,

通过上述的再反思,学生不仅发现了自己思维过程中的不足之处,从而完善了解题过程,同时也提高了他们发现问题的能力,训练了思维的严密性和批判性,有利于养成严谨细致的学习习惯.

二、反思题目特征,理清条件与结论的关系

解完一道题后,通过反思题目特征,研究条件与结论之间的必要性或充分性,或借变式探究更一般性的结论,可以加深对题目本质的领悟,从而获得一系列的思维结果,有助于培养学生思维的深刻性和广阔性.

例二如图3,梯形ABCD中,AB//CD,∠ABC=90°,AB=BC=5,DE=4,∠EAD=45°.求△AED的面积.

图3

图4

解:构造正方形ABCF,将△AFD绕点A旋转90°到△ABG的位置,如图4,易证G、B、C三点共线,且△AEG～=△AED,EG=ED=4,所以,△AED的面积等于△AEG的面积,等于

事实上,这是一道错题,设DF=x,由DE=BE+DF知,BE=4−x,EC=x+1,DC=5−x,在Rt△DCE中,(5−x)2+(x+1)2=42,化简,得x2−4x+5=0,显然Δ＜0由知,题目中所给数据矛盾,题目出错.

以上类似的错误,在教学过程中,其实很常见,而出现这样错漏的原因也很复杂,有客观、主观原因,或由时间环境导致,更有教学水平高低因素等.如下例:

例三已知△ABC中,A(3,6)、B(−2,1)、C(1,4),求BC边中线AD的长及∠A平分线AE的长.

再反思:∵kAB=kAC,∴A、B、C三点共线,它们不能构成三角形.误解中用代数计算的方法掩盖了三角形不存在的事实,这也是一个错题.

三、反思解题方法,寻求最佳方案

解题是学生往往满足于做出解答,而对自己解题方法的优劣却不加分析,作业中经常出现解题方法单一,思路狭窄,过程繁琐,缺乏灵活性的情况.因此教师必须引导学生评价自己的解题方法,努力寻找解决问题的最佳方案.

例四已知抛物线C1∶y=2x2−3x−5与抛物线C2∶y=−x2−x+4交于点A、B,求直线AB的解析式.

解:先分别求出A、B点坐标,消去y,得

以上求解直线方程的过程,计算显然比较繁琐;有没有较好的方法呢?我们作进一步的研究,下面的方法显然能够避免繁琐的计算,通过巧妙设置经过交点A、B的“函数图像系”,即可轻松求得正确的结果.设所求直线AB的解析式为:

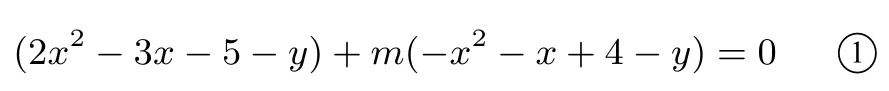
当2−m=0时,m=2,①式变为直线AB的解析式:

四、反思问题本质,及时进行推广

解决问题以后再重新剖析其实质,可使学生比较容易地抓住问题的实质,在解决了一个或几个问题以后,启发学生进行联想、类比,揭示问题的一般规律.

例五.如图5,已知AD是△ABC的高,∠BAC=45°,BD=2,DC=3.求AD的长.

略解与反思:如图6,原题是将△ADB、△ADC分别沿直线AB、AC翻折到△ABE、△AGC的位置,得到正方形AEFG,最后利用勾股定理可求得AD=6.

再探索的问题是,如果将∠BAC=45°改为60°或75°或120°或150°呢?能否改为更一般的角度呢?其实答案是肯定的.

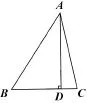
图5

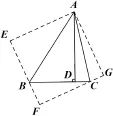
图6

事实上,按原题辅助线的作法,解决变更角度后的问题,也是可行的,只不过要用到余弦定理等超纲内容,如果换一个思路探索,我们可以得出更一般化的结论.设∠BAC=α, 0°＜α＜90°.

图7

以上从四个方面,简单介绍了解题后再反思的点滴做法.这种再反思显然能提高课堂教学效果,发展学生数学能力,我们在教学中要坚持让学生独立思考,培养学生在解题后对解题思维过程进行再反思的学习习惯.