广东省汕头市潮阳区谷饶中学(515159) 张应武

培养中学生数学应用能力的一点做法

广东省汕头市潮阳区谷饶中学(515159) 张应武

数学源于实践又服务于实践,数学理论是人们在研究世界的空间形式和数量关系的过程中,通过科学的抽象而逐步发现和发展的,它具有准确性、严密性、逻辑性和抽象性等品格,但它之所以能长盛不衰不断发展,主要还是由于它能用来解决实际问题.在平时的教学过程中,很多老师都有这种感觉:许多学生尽管对解决纯数学问题得心应手,然而一旦遇到实际问题便束手无策,而当教师把这些问题转化为数学模式,用数学语言加以表述后,学生便恍然大悟,很快解决问题.原因就在于数学教学只偏重对具体数学形式和技巧的盲目追求,忽视了对学生应用数学知识能力的培养,使得相当多的中学生未能接受到他们所需要的数学教育.

数学的学习就不仅只是为了升学的需要,而更主要的是为学生的生活和就业提供必要的数学知识和技能.因而在具体的教学实践中,教师就需要教给学生把实际问题转化为数学问题的方法,有意识地对学生进行数学实践能力的培养,使学生能够学以致用,让学生真正感受到数学的价值,从而激发他们努力学习数学的兴趣和动力.

要培养学生运用数学方法解决实际问题的能力,就要在学生认真掌握好数学基本概念、基本知识和基本技能的基础上,大力加强数学应用题的教学,培养学生对实际问题进行数学抽象的能力,教会学生把表述实际问题的自然语言翻译为数学语言.在此基础上,在适当的时间和适当的场合,介绍数学史上将实际问题转化为数学问题的一些实例,能大大提高学生学习数学的兴趣,激发他们的学习积极性和主动性,使他们的数学应用能力得到进一步强化.现举例说明.

例1博尔达计分法问题

在一次选举中,共有四位选民和五位候选人,选民依他们对候选人喜好的程度,将候选人从上到下排列如下表,问哪一个当选?

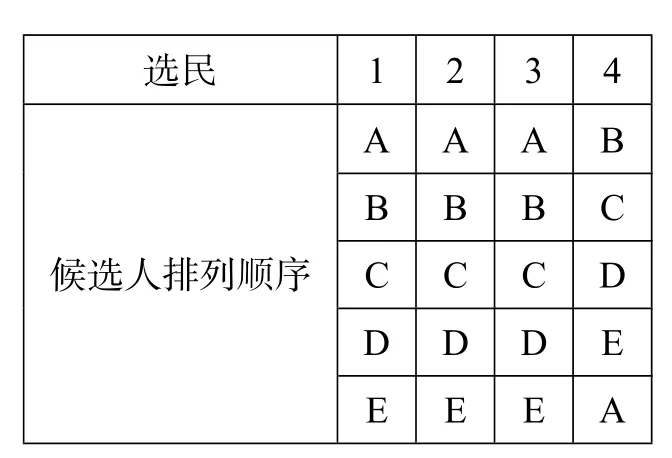
选民1 2 3 4 A A A B B B B C候选人排列顺序C C C D D D D E E E E A

解决这个问题主要是要给出理由依据,即把这个问题数学化,也即量化,但如何数学化呢?

1770年法国数学家博尔达(Jean Charles de Borda)提出一套排列候选人顺序的计分办法.博尔达计分法的操作,可用下面的表格来说明.在表格中,共有四位选民和五位候选人,选民依他们对候选人喜好的程度,将候选人从上到下排列,排列在越高位置的候选人,得分越高.

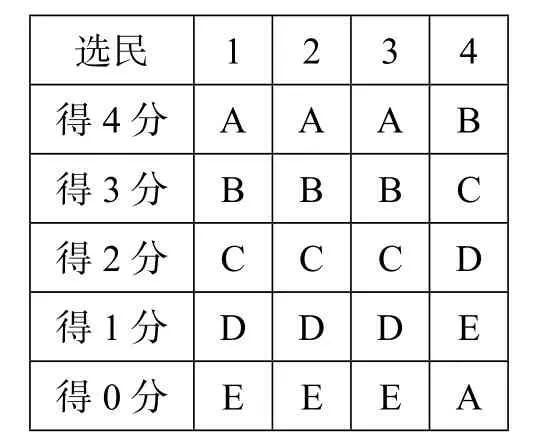
选民1 2 3 4得4分A A A B得3分B B B C得2分C C C D得1分D D D E得0分E E E A

候选人A共得12分,B得13分,C得9分,D得5分,E得1分.因此,根据博尔达计分法,最理想的排列顺序是:B, A,C,D,E.

这个问题能推广到n个村民选举m个候选人的一般情况,只需把得分修改就行.

这种方法用到的知识不是很高深,但却能解决问题,即把问题转化为数学问题,能够调动学生的学习兴趣.这种方法还能够推广,如有四只宝马A、B、C、D进行4轮的比赛,成绩如下:

轮次名次①②③④23 B 2 142 C 4 411 D 3 234 A 13

问:哪一只宝马比较好?

按照博尔达计分法可以这么操作:第一名得3分,第二名得2分,第三名得1分,第4名得0分,则A得7分,B得7分,C得6分,D得4分.A和B的成绩一样.我们可以改变得分:第一名得5分,第二名得3分,第三名得1分,第4名得0分,则A得10分,B得11分,C得10分,D得5分.这样B是成绩最好的.

同样,这个问题也可以推广到一般的情况(n只马进行m次的比赛).

问题还可以推广到团体的总积分的计算,如计算一个体育代表团的总积分问题(给第一名、第二名、第三名等赋相应的值就可以计算了).

例2哥尼斯堡七桥问题

图1

在18世纪,普鲁士的哥尼斯堡城(现立陶宛共和国)的许多人热衷于一个难题:在哥尼斯堡镇有一个岛,普雷格尔河两支绕流其旁,七座桥a,b,c,d,e,f,g跨这两条支流(如图1所示).问:一个人怎样走,才能一次走遍七座桥,且每座都只经过一次.很多人都想解决这个难题,但年复一年,谁也找不到答案.这个问题表面看起来跟数学毫不相干,但是数学大师欧拉却在1736年用数学方法证明了这样的走法是不存在的.欧拉的方法非常巧妙,也非常简单.他发现,在这个问题中A,B,C,D四块陆地的大小和桥的长短、河的宽窄等都无关紧要,因而A,B,C,D可以抽象为平面上的四个点,而七座桥可以抽象为连接这四个点的线条,如图3这样,问题就变为:能否一笔画出图3中的图形,即笔不离纸,每个点、每条线都经过,且每条线都不重复?

欧拉把像图3那样由若干个点和连接这些点的若干条线组成的图形称为“网络”,把线的交点叫“顶点”.如果一个顶点有奇(偶)数条线相交,这个顶点就叫做奇(偶)点.欧拉证明了:一个网络能够一笔画出的充要条件是该网络中奇点的个数是0或2.显然,图3中4个顶点都是奇点.所以图3不可能一笔画出来,即满足原题中条件的走法是不存在的.这种方法导致了一门崭新的数学分支——图论(起初欧拉称为位置几何学)的诞生,也为拓扑学的建立奠定了基础.图论和拓扑学的发展,又为生产、生活和科学研究中的各种新问题的解决提供了强有力的数学工具.

例3斯坦纳最短距离问题

1 9世纪的德国数学家斯坦纳根据生产实践的需要,研究了一个看起来虽然简单,但却很有实用价值的问题:在三个村庄之间建立一个供水站,为了让用水的人方便,并且所用水管最省,问:怎样确定供水站的位置?

换成数学语言就是:设A,B,C是平面内不在同一直线上的三点,求△ABC内的一点M,AM+BM+CM最小.

这个问题还可以推广为:在A,B,C三个村庄间建一座供水站,已知通往各个村庄的水管造价分别为(单位:元／米)m,n,r,问供水站应建在何处,才能使总造价最低?换成数学语言就是,在△ABC内求一点M,使mAM+nBM+rCM最小.

问题还可变化为:设A,B,C三个村庄分别有学生200人,300人,400人要在三个村庄间建立一所学校M,使所有学生在上学时所走的总路程最短.

换成数学语言就是:在△ABC中求一点M,使200AM+300BM+400CM最小.

尽管上述三个问题各有不同的实际意义,但化为数学语言后可以看出,它们的实质都是同一个数学问题:设m,n,r为常数,在△ABC内求一点M,使mAM+nBM+rCM最小.第一个问题是的特殊情形.

数学的强大功能之一,就在于它能将形式各异的实际问题抽象出共同的本质特征,而用相同的数学方法来解决不同的实际问题,如何从自然语言到数学语言是转换的关键,在于把三个村庄、供水站或学校抽象为平面上的三个已知点和一个未知点;把连接村庄的水管或学生所走的路径,抽象为连接点的线段.实际问题化为数学问题,就能够运用相应的数学知识加以解决.

从以上几个实例可以看出,把实际问题转化为数学问题的关键,在于把表述实际问题所用的自然语言翻译成数学语言.而要做到这一点,就需要进行相应的数学抽象.

此外,还可以向学生介绍“航船相遇问题”、“韩信点兵”、“狱吏问题”和其他典型例题,也能大大激发学生学习数学的兴趣和动机,改变他们对数学“抽象”、“神秘”、“无用”的看法,消除他们对解决应用题的畏难情绪,让他们转而迷恋应用题,从而形成数学学习的良性循环.

日本教育家杉山吉茂先生说过:“数学带有人类社会有价值的东西,因此数学必须有用途和益处,这种用途和益处本来是应该教应该学的,可是在教学过程中往往忘掉这一点而陷入技能的熟练之中,使人感到数学是讨厌的、是与自身无关的思维游戏而已”.数学的教学实践说明,教师在教学中充分注意引导学生去追求数学的价值和美,必定能够促使学生对数学产生极大的学习欲望,而不再停留于为应付升学考试去死记硬背数学概念、公式、定理.这样,无论他们将来继续升学与否,数学都会使他们受益终生.

[1]张卿,妙趣横生的数学难题[M],天津:天津人民出版社,1980.