☉江苏省高淳高级中学祝辉

漫谈函数奇偶性

☉江苏省高淳高级中学祝辉

初中函数教学并没有给拥有特殊对称的函数以性质界定，但在几何教学中给出过轴对称和中心对称的概念.从图形上来讲，轴对称和中心对称是学生比较认可的美学特征，但是高中函数奇偶性却让不少学生认识到了函数性质的抽象性，成为学生学习不小的障碍.从教学现状来看，奇偶性教学更多地是依赖判别标准判断函数奇偶性，而往往缺失了对奇偶性观察、思考、理解、实验.而这些却恰恰是奇偶性性质教学的灵魂.

苏教版主编单墫先生多次在不同场合对“如何教？为什么这样教？教学功利性？”等问题提出过不少建议：我们的教学大都是本末倒置的，课堂上应该花百分之七十的时间理解教材，分析例题，想一想为什么选用这样的例题？如何将浓缩的教材知识给予好好的稀释.但是现阶段教学却是花百分之三十的时间在教材上草草了事，花更多的时间在做教辅资料，这种教学根本没有理解数学.笔者认为，从课程标准的角度来说，显然后者的教学是令人担忧的.那么如何上好一节课？如何将形式化的函数奇偶性演绎得通俗易懂？本文从案例的角度抛砖引玉跟大家交流，恳求读者指正.

一、实验绘制

奇偶性概念是比较抽象的，尤其对于刚刚接触抽象概念的高一新生来说，直接使用形式化的数学语言会让学生难以理解.笔者采用了一个课前动手实践的方式，首先从生活中获取感性认识.

布置课前预习作业：

（1）请找到生活中四种不同的具备轴对称、中心对称特性的物品；

（2）请找到四种不完全对称的物品；

（3）请绘制四个不同的具备轴对称、中心对称的函数图像；

图1

（4）绘制四个不具备对称性的函数图像.生：找到了一些物品，比如蝴蝶、银行的标记、中国古代的太极八卦、中国移动的标记，分别存在轴对称和中心对称.还用几何画板画了一些函数，比如y=x2，y=x+等等.

师：这些图形和函数不仅具备了一定的美感，而且在研究这样的图形或函数时，我们可以只需要花一半的时间进行研究即可，这也为为我们很多的生活运用，诸如利用对称建造房屋等减少了设计精力.

设计意图：图1为学生找寻的具备对称美的物品和函数.用学生亲身的体验和思考，感受生活中的对称美，以及所学函数中具备对称美的函数.选择具备对称性和不具备对称性都自主探索的原因是，为后续理解奇偶性概念中“任意”两字作好铺垫，也暗示了学习奇偶性的目的——花一半的力气研究整个函数.

二、课堂交流

有了课前的探索和思考，请学生对比交流各自找到的具备对称性的物品或函数，特别要请学生说一说不具备对称性的物品或函数为什么不具备对称性？（给出学生找到的不具备对称的物品或函数数例）

生：从图2我们发现，要对称的物品或函数必须处处存在对称性，而那些不具备对称性的物品或函数，只需要某一处不对称就可以了.比方说，被虫咬过的树叶，左边存在破损处而右边完好无损，所以显然是不对称物品.

师：好.这种不对称体现在某一处即可，大家观察得很仔细.相比需要对称，要说明没有对称性显得非常容易.请同学们来总结下轴对称和中心对称的表述.

设计意图：本课的设计用了大幅学生作品，既从情感上让学生感到所学所做有一定的价值，又潜移默化中让学生感受：对称是需要处处对称的（即数学语言“任意性”渗透），不对称只需要找到一处不对称即可（即数学语言“存在性”渗透）.

三、建构概念

生：轴对称可以这样表述：存在一条直线，可以让图形关于这条直线翻折完全重合.

师：这是一种感性的表述，我们将其对应f（x）=x2来进行函数轴对称的数学归纳.

生：只需要函数在对称轴左边每一个点关于直线都有对应点，这样的函数具备了轴对称.

师：好！“每一个点”这句话说得很到位！今天我们先给对称轴为y轴的函数抽象成精准表述：对任意的自变量x∈D（定义域），都有f（-x）=f（x），称函数f（x）为偶函数.（需要注意：偶函数是一种特殊的对称函数，其关于y轴对称）同样，你能表述中心为原点的中心对称函数的概念吗？

生：对任意的自变量x∈D（定义域），都有f（-x）= -f（x），称函数f（x）为中心在原点的中心对称函数.

师：是的.中心在原点的中心对称函数，我们称其为

奇函数.有了这两种最为特殊的对称函数模型，以后研究其他对称函数模型，无非是平移的问题了.任意性这三个字，同学们从图形中都理解到位了，那么转换为更通俗易懂的数学知识对应了你学过的哪一个知识点呢？

生：左右两边要完全一样！应该是每一个点对应！也就是三要素中最基本的定义域需要满足对称性！

师：说得很好！即定义域需要关于原点对称！这是解决奇偶性的第一步！若定义域为［-2，1］呢？你想想会怎么样？

生：图形肯定不对称！从上面我们举出的一系列物品和函数图像就可以知道！

设计意图：这样的作法让学生对于概念中“任意”两字的理解迅速到位，为后续解决奇偶性问题作好铺垫.

四、小试牛刀

试题类型（一）

①f（x）=x3，x∈R；②f（x）=x2，x∈［-2，2］；

③f（x）=x2-1，x∈［-2，2）；④f（x）=x3-x，x∈（0，+∞）.

设计意图：从概念出发，判别基本初等函数的单调性.从两个方面入手：第一是定义域的观察；其次是概念代数属性运用：f（-x）=-f（x）或f（-x）=f（x），也可以从图形的角度作图判断.

试题类型（二）

设计意图：从复合函数的角度入手，给出了几个复杂函数模型，从定义的角度入手，利用f（-x）=-f（x）或f（-x）=f（x）的变形式解决问题.对于学生而言，复杂函数或复合函数奇偶性需要善于应用表达式的变形，让学生灵活体会不同函数模型选择不同表达式变形的处理技术.

试题类型（三）

①f（x）=g（4+x）+g（4-x）（x∈R）；

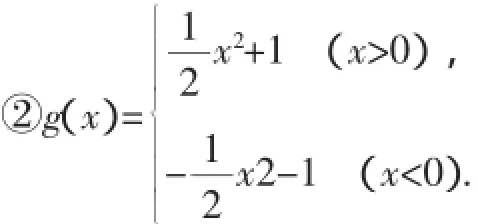
设计意图：试题选择的最高层次是面向抽象函数和分段函数的使用，我们知道在抽象函数中使用奇偶性定义判断是一个难点，鉴于具体表达式的缺失，导致学生判断时易出现问题；分段函数更是难点，因为对于表达式f（-x）=-f（x）或f（-x）=f（x）而言，每次需要选择不同的表达式，这一点学生往往缺乏正确的判断，教学中将这一环节弄清楚，可以破解分段函数奇偶性.下面给出简要分析：

①它具有对称性，因为（f-x）=g（4-x）+g（4+x）=（fx），所以（fx）是偶函数，不是奇函数.

五、后续

奇偶性是函数性质的难点和重点，通过上述感性认知——理性总结——巩固训练，我们不难发现，学生对于奇偶性概念的理解和运用比传统启发式教学有了更高的认识，主要体现在：

（1）实验探索来说，让学生感受了数学背景下的物品，体现了数学之用，更让学生感受了生活中无处不在的对称美；从感受中又提炼了隐藏于物理属性下数学本质——轴对称和中心对称，让学生理解上升了一个思想层次.

（2）任意性理解来说，奇偶性定义中最难的是任意性的理解，通过实验我们发现，学生对于“任意性”的理解非常到位，即判断奇偶性第一准则需要考查定义域的对称性，若定义域没有对称性，则一定是非奇非偶函数.

（3）教学的新思考：以往的教学往往是在课堂上探索对称性，笔者并不认同，从教学成熟性角度来说，笔者建议这些探索以二十分钟实验的方式作为预习阶段实现，这样的好处既不用匆匆忙忙在课堂教学中去实现这一探索，也让整个教学不处在一直“追赶”的环节中，实现了课堂教学的充分性.

1.杨玉东，范文贵.高中数学新课程理念与实施［M］.海口：海南出版社，2011.

2.柴贤亭.数学教学中的问题设计［J］.教学与管理，1999（10）.

3.沈恒.浅谈中学数学课堂教学的适度形式化［J］.中小学数学，2010（5）.Z