王爱法

(重庆理工大学 理学院，重庆　400054)



分裂左GC-lpp 半群的+-同余

王爱法

(重庆理工大学 理学院，重庆400054)

利用分裂左GC-lpp半群的分件半群上的同余所构成的同余对L和R来构造此类半群上的+-同余,并证明这种半群上的所有同余作成的集合在文中定义的偏序关系下是完备格。

左GC-lpp半群; 左正则带; 同余

1982年,Blyth和McFadden在文献[1]中首次引入了正则半群的乘法逆断面。EI-Qallali在文献[2]中引入了与乘法逆断面类似的适当断面。随后,Chen和Guo在文献[3-6]中分别研究了含有适当断面的富足半群的子类。文献[7-9]分别研究了含有逆断面的正则半群的同余。最近笔者在文献[10]中利用含有SQ-适当断面S°的富足半群的分件半群上的同余所构成的同余三元组L、T和R来构造此类半群的*-同余。在文献[6]中,Li、Guo和Fu给出了分裂左GC-lpp半群的结构定理。本文利用裂左GC-lpp半群的分件半群上的同余所构成的同余对L和R来构造此类半群的+-同余并证明了在这种半群上的所有同余作成的集合在文中定义的偏序关系下是完备格。

1　预备知识

设S为半群,定义aR*b，对于所有的x,y∈S1,xa=ya当且仅当xb=yb。对偶地可定义L*。根据R*和L*的定义易得5*是左同余,L*是右同余。若a和b是S中的正则元，则当aR*b且仅当aRb。

设S为半群,若S的每一个R*-类含有一个幂等元,则称S为左富足半群。对偶地可定义右富足半群。由文献[11]知,若S既是左富足半群又是右富足半群,则称S为富足半群。

设S为左富足半群,若S满足:

1)E(S)是左正则带;

2) 对于所有的a∈S,e∈E(S),有ae=(ae)+a。

则称S为左GC-lpp半群[12]。 若正则半群S的E(S)是带,则称S为纯正半群。若纯正半群S的每一个R*-类只有一个幂等元,则称S为R-幂幺半群。由以上3种半群的定义知：左GC-lpp半群是左ample半群和R-幂幺半群的推广。

设S,T为半群,φ为S到T的同态映射,若φ满足:

1) 若aR*b,则aφR*bφ;

2) 若aR*b,则aφR*bφ。

则称φ为S到T的好同态。若φ为满射且存在从T到S的好同态φ使得φφ=idT(其中idT是T上的恒等映射),则称φ是分裂的。设ρ为半群S上的同余,若由ρ诱导的从S到S/ρ的自然同态ρb是好同态,则称ρ为S上的好同余。

设B为带：

1) 若对于任意的x,y∈B,xy=xyx，则称B为左正则带；

2) 若对于任意的x,y∈B,xy=yxy，则称B为右正则带；

3) 若对于任意的x,y∈B,xyzx=xyxzx，则称B为正则带；

4) 若对于任意的x,y∈B,xyzw=xzyw，则称B为正规带。

引理1[11]设e∈E(S),a∈S，则eR*a，当且仅当ea=a且对于所有的x,y∈S1,有xa=ya⟹xe=ye。

以下假设:

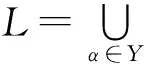
若φ满足以下条件：(Q1)φ是半群同态; (Q2) 对于所有的a∈T,x∈Lα,有φax∈L(aα)。且在半群L中,若x∈Y,则φax=(ax)+; 若a∈Y,则φax=ax。则称四元组(Y,T,L;φ)是GC-系统。

在GC=GC(Y,T,L;φ)={(x,s)∈L×T|s∈T,x∈Ls+}上定义乘法为

按照这样定义乘法是有意义的并且GC在上面的乘法下是闭的。

引理2[6]设(Y,T,L;φ)是GC-系统。则GC=GC(Y,T,L;φ)是含有左适当断面GC°={(s+,s)∈T}的左GC-lpp半群并且同构于T；反之,每一个含有左适当断面的左GC-lpp半群都可以按照这种方式来构造。

引理3[6]设GC=GC(Y,T,L;φ)是GC-系统,(x,s)∈GC，则(x,s+)∈E(GC)并且(x,s)R*(x,s+)。

引理4[6]若S是左GC-lpp半群,则S是分裂半群，当且仅当S有左适当断面。

2　半群的+-同余

定义1设S为左富足半群,ρ为S上的同余。若对于所有的a,b∈S,aρb⟹a+ρb+，则称ρ为S上的+-同余。

以下例子基于文献[12]中的命题2.3。

例1设S是以Y为半格的左适当半群。

则μR是包含在R*中的最大同余。易证μR是S上的+-同余。

例2设S是左型-A半群,τ是由R*生成的S上的同余。显然，aτb当且仅当a+τb+，因此，τ是S上的+-同余。

设T是以幂等元集Y为半格的左型-A半群,L是以Y为骨架的正则带,ρL为L上的同余,πT为T上的+-同余。若以下条件成立:

(C.1)ρL|Y=πT|Y;

(C.2) (∀s,t∈T)(∀m∈L)sπTt⟹s+(φsm)ρLt+(φtm);

(C.3) (∀l∈T)(∀m,x,u∈L)xρLu⟹m(φlx)ρLm(φlu)。

则称(ρL,πT)为GC上的+-同余。

在GC上定义二元关系ρ(ρL,πT)为(x,s)ρ(ρL,πT)(u,t)⟺xρLu,sπTt。

定理1设GC为形如引理1.2中含有左适当断面的左GC-lpp半群,(ρL,πT)为GC上的+-同余对，则ρ(ρL,πT)是GC上的+-同余。反之,GC上的每一个+-同余都可以按照以上方式来构造。

证明显然ρ(ρL,πT)是GC上的等价关系,下证ρ(ρL,πT)是GC上的同余。

假设(x,s),(u,t),(m,l)∈GC，(x,s)ρ(ρL,πT)(u,t)，则xρLu,sπTt。由xρLu和(C.3)可得m(φlx)ρLm(φlu)。因为πT是+-同余,所以lsπTlt。从而可得

即

由sπTt和(C.2)可得s+(φsm)ρLt+(φtm),从而有x(φsm)ρLu(φtm)。再由πT是+-同余得slπTtl,因此(x(φsm),sl)ρ(ρL,πT)(u(φlm),tl),即

故ρ(ρL,πT)是GC上的同余。

若(x,s)ρ(ρL,πT)(u,t),则xρLu,sπTt。因为πT是+-同余,所以s+πTt+，从而可得(x,s+)ρ(ρL,πT)(u,t+)。因此ρ(ρL,πT)是GC上的+-同余。

反之,假设ρ是GC上的+-同余，在L和T上分别定义二元关系ρL和ρT为:

由于完全抗剪连接的FCB梁结合面滑移很小，测试精度较差，故本试验仅对部分连接结合梁(PCB梁)进行了钢梁与混凝土板之间结合面的相对滑移测试，图8给出了不同质量试验车辆以2 m/s通过PCB梁时支座位置结合面的滑移时程曲线。

因为ρ是GC上的+-同余,所以ρL是L上的等价关系,ρT是T上的等价关系。

设(x,s),(u,t),(p,o),(m,l)∈GC。若xρLu,pρLm,则(x,s+)ρ(u.t+)和(p,o+)ρ(m,l+)，从而可得(x,s+)(p,o+)ρ(u,t+)(m,l+)，因此

再利用(Q2)可得(xp,s+o+)ρ(um,t+l+)，所以xpρLum。显然ρL|Y=πT|Y,故(C.1)成立。

设sρTt,则(s+,s)ρ(t+,t)，从而(s+,s)(m,l)ρ(t+,t)(m,l),即

因此s+(φsm)ρLt+(φtm)，故(C.2)成立。

设(m,l)∈GC,x∈Ls+,u∈Lt+,xρLu,则(x,s+)ρ(u.t+)，从而

即

因此m(φlx)ρLm(φlu),故(C.3)成立。

由以上证明可得(ρL,ρT)是GC上的+-同余对。显然ρ(ρL,ρT)是GC上的+-同余。若(x,s)ρ(ρL,ρT)(u,t),则xρLu,sρTt，故

从而

即(x,s)ρ(u,t)。 故ρ(ρL,ρT)⊆ρ，而ρ⊆ρ(ρL,ρT)是显然的,所以ρ(ρL,ρT)=ρ。

例3设M={1,x,e}在M上定义乘法为:

M1xe111exxxeeeee

易证M为半群。若令Y={1,e},则Y为半格。显然,I1={1,x},Ie={e}是M的所有左零正则带。通过计算可得M是以Y半格为骨架的左正则带。

例4设A是由a生成的无限循环群,B是由b生成的无限循环幺半群,其中e为B的恒等元，将A和B分别记作:

其中b0=e，令S=A∪B∪{1},在S上定义乘法如下:

1)am1am2=am1+m2,其中am1,am2∈A;

2)bn1bn2=bn1+n2,其中bn1,bn2∈B;

3)ambn=am+n,其中am∈A,bn∈B;

4)bnam=bn+m,其中bn∈B,am∈A。

易得S是含有幂等元1和e的幺半群。S的R*-类为:A∪{1},B;L*-类为:{1},A∪B，因此S是适当幺半群。进一步可得,对于S中的所有幂等元x和S中的所有元素s有sx=(sx)+s，故S是左型-A半群。

以下将给出一个含有左适当断面的左GC-lpp半群的+-同余的例子。

例5设S={(1,1),(1,al),(x,am),(x,1),(e,bn)|l,m,n∈Z且l>0,m>0,n≥0},S上的乘法如下所示：

S(1,1)(1,al)(x,am)(x,1)(e,bn)(1,1)(1,1)(1,al)(1,am)(1,1)(e,bn)(1,al1)(1,al1)(1,al1+l)(1,al1+m)(1,al1)(1,al1+n)(x,am1)(x,am1)(x,am1+l)(x,am1+m)(x,am1)(x,am1+n)(x,1)(x,1)(x,al)(x,am)(x,1)(e,bn)(e,bn1)(e,bn1)(e,bn1+l)(e,bn1+m)(e,bn1)(e,bn1+n)

易证S是半群并且E={(1,1),(x,1),(e,e)}是左正则带。从表中可得S的R*-类是：{(1,1),(1,al)|l>0},{(x,am),(x,1)|m>0},{(e,bn)|n≥0}。还可证得对于所有的a∈S和e∈E,有ae=(ae)+a。因此，S是左GC-lpp半群。

容易验证T={(1,1), (1,al),(e,bn)}是S的左适当断面。此外还可得等价关系1S和σS是S上的+-同余,其中1S和σS对应的等价类分别是:

1S:{(1,1)},{(x,1)},{(e,e)},{(1,a)},{(1,a2)},…{(x,a)},{(x,a2)},…,{(e,b)},{(e,b2)},…;

σS:{(1,1)},{(x,1)},{(e,bn)n≥0},{(1,al)|l>0},{(x,am)|m>0}。

3　+-同余格

用C(GC)表示GC上+-同余的全体,CT(GC)表示形如定理1中GC上+-同余的全体。

证明充分性是显然的,下面看必要性。

命题1设Ω⊆C(GC),Tρ=(ρL,ρT) (其中ρ∈Ω)，则

证明第1个等式显然成立,因此只需证明第2个等式。

结合上面的结果可得到下面的定理：

定理2设GC是形如引理2中的半群,则CT(GC)在文中定义的偏序下是完备格，且C(GC)和CT(GC)作为完备格是同构的。

[1]BLYTH T S,MCFADDEN R.Regular semigroups with a multiplicative inverse transversal[J].Proceedings of the Royal Society of Edinburgh:Section A Mathematics,1982,92(3/4):253-270.

[2]El-QALLALI A.Abundant semigroups with a multiplicative type A transversal[C]//Semigroup Forum.Springer-Verlag:[s.l.],1993,47(1):327-340.

[3]CHEN J C.Abundant semigroups with adequate transversals[C]//Semigroup Forum.Springer-Verlag:[s.n.],2000,60(1):67-79.

[4]GUO X J.Abundant semigroups with a multiplicative adequate transversal[J].Acta Mathematica Sinica,2002,18(2):229-244.

[5]GUO X,WANG L M.Idempotent-connected abundant semigroups which are disjoint unions of quasi-ideal adequate transversals[J].Algebra,2002,30(4):1779-1800.

[6]LI Z Z,GUO X J,FU Z Q.Split Left GC-Lpp Semigroups[J].Journal of Mathematical Research with Applications,2012,32(1):33-42.

[7]WANG L M.On congruence lattice of regular semigroups with Q-inverse transversals[J].Semigroup Forum,1995,50:141-160.

[8]TANG X,WANG L M.Congruences on regular semigroups with inverse transversals[J].Communications in Algebra,1995,23(11):4157-4171.

[9]WANG L M,TANG X.Congruence lattices of regular semigroups with inverse transversals 1[J].Communications in Algebra,1998,26(4):1243-1255.

[10]WANG A,WANG L.*-congruences on abundant semigroups with SQ-adequate transversals[J].Acta Mathematica Hungarica,2013,141(4):358-365.

[11]FOUNTAIN J.Abundant semigroups[J].Proceedings of the London Mathematical Society,1982,3(1):103-129.

[12]FOUNTAIN J.Adequate semigroups[J].Proceedings of the Edinburgh Mathematical Society (Series 2),1979,22(2):113-125.

(责任编辑陈艳)

+- Congruences on Split Left GC-Lpp Semigroups

WANG Ai-fa

(School of Science, Chongqing University of Technology, Chongqing 400054, China)

We gave +-congruences on a split left GC-lpp semigroup by the +-congruence pair abstractly which consists of congruences on the structure component partsLandR. We proved that the set of all congruences on this kind of semigroups is a complete lattice.

left GC-lpp semigroup; left regular band; congruence

2016-03-26

重庆市教委科学技术研究项目(KJ1500925，KJ1600930)

王爱法(1980—)，男，山东泰安人，博士研究生，讲师，主要从事半群及半环代数理论研究，E-mail:wangaf1980@163.com。

format：WANG Ai-fa.+- Congruences on Split Left GC-Lpp Semigroups[J].Journal of Chongqing University of Technology(Natural Science)，2016(8):143-147.

10.3969/j.issn.1674-8425(z).2016.08.023

O152.7

A

1674-8425(2016)08-0143-05

引用格式：王爱法.分裂左GC-lpp 半群的+-同余[J].重庆理工大学学报(自然科学)，2016(8):143-147.