翟悦涵

⦿ 哈尔滨师范大学教师教育学院

数学学习是认识、理解、掌握和运用知识的过程,旨在为实际生活提供服务.然而,解决问题的创造性活动要求学生的数学思维更加发散和深刻.但是,在教学实践中,许多学生常常由于思维不够灵活而在分析、思考和解决问题时遇到困难,例如:不懂得如何分析数学问题,无法建立明确的数量关系,无法形成清晰的解题思路,等等.因此,在初中数学教学中,教师应该基于学生在解题过程中遇到的思维障碍,通过必要的思维训练,帮助学生疏通解题思路,循序渐进地提高他们的数学解题能力.

1 初中生数学解题思维障碍分析

相比其他学科,数学具有更强的逻辑性和抽象性,这对学生的综合能力和思维能力提出了更高的要求.然而,在传统的机械化和重复性训练中,学生的解题思维往往难以拓展,导致他们在解题时频繁遇到困难.第一,逆向思维能力薄弱.学生习惯于正向思维,很少运用逆向思维来分析和解决问题.一旦遇到困难,就无从下手.第二,存在思维盲点.由于数学学科的特点,数学问题对学生的思维广度和深度提出了较高要求.然而,初中生在实际解题中存在很多思维盲点,导致他们在思考和分析问题时会遇到许多障碍.第三,存在思维惰性障碍.数学解题实际上是一种思维活动.但在实际解题中,一些学生常常受到惰性思维的影响,遇到一点困难就停滞不前.在这种思维障碍下,即使遇到关键信息,他们也无法深入思考,难以形成明确的解题思路.第四,存在定势思维障碍.数学学科对学生的思维灵活性和广度提出了更高要求.然而,在实际解题训练中,受到“只解此题”教学模式的限制,学生常常表现出定势思维,难以找到解题的新视角和突破口.同时,在这种定势思维的影响下,学生还经常陷入解题的误区,导致出现各种错误[1].

2 初中数学解题的基本思维模式

对于数学学科而言,解题思维具有一定的规律.常见的初中数学解题思维主要包括转化思维、联想思维、整体思维和逆向思维.其中,转化思维是指通过改变问题的方向,将未知问题转化成为熟悉的数学知识或具体、形象的问题.这种思维在数学解题中经常出现,学生需要掌握这种思维才能灵活解决问题.联想思维是从已知条件、图形或所求题目等方面联想到相关的定义、定理或法则,并由此形成解题思路.在解决难题时,联想思维可以引发灵感,使问题更加清晰.整体思维是指从整体入手,将彼此孤立的问题视为一个整体,通过设元、变形和代入等方式解题.整体思维可以摆脱“单一未知量”的限制,简化复杂的数学问题,提高解题效率.逆向思维是指改变思考角度,以所求结论作为起点,通过逆向考虑的模式回到已知条件中.这种“倒着干、反向考虑”的模式,即为逆向解题思维.

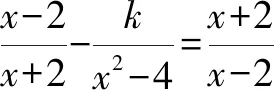
针对此题,根据增根的定义可知,只有当分式方程的最简公分母不等于零的时候,分式方程才不会产生增根.但在该分式方程中,最简公分母(x+2)·(x-2)≠0的x值有很多,无法逐个代入进行求解.针对这一现象,在优化解题时,可引领学生改变思维的角度,从结论出发,以题目所求结论的对立面为出发点,围绕“会产生增根”展开反向思考,逐渐找出产生增根的k值,即可得到不会产生增根的k值.

将方程两边同时乘最简公分母(x+2)(x-2),得(x-2)2-k=(x+2)2.

只有当(x+2)(x-2)=0时,方程会产生增根.

此时x=2或x=-2.

将x=2,x=-2分别代入(x-2)2-k=(x+2)2中,得k=±16.

即当k=±16时,方程会产生增根.

所以,当k≠±16时,原分式方程不会产生增根.

可见,在解决例1时,转变了传统从条件到结论的顺序,坚持逆向思维,从结论的反面出发进行思考,最终实现了化繁为简、化难为易,真正提升了学生的数学解题能力[2].

3 初中数学解题中思维品质培养路径研究

3.1 合理渗透数学思想

数学概念、公式和定理的产生过程中都蕴含着数学思维和数学思想方法.这些思维和方法通常零散地分布在教材的各个章节中.因此,教师在课堂教学中不能只讲授知识点,还要深入挖掘其背后蕴含的数学思想和方法.通过精讲和细讲,借助数学概念和定理的形成过程以及一些例题,将这些思维和方法传授给学生.例如,在“有理数加法法则”教学中,可以利用问题串,有意识地渗透分类讨论思想、数形结合思想;在“相似三角形性质”教学中,可利用“相似多边形面积比和相似比的关系”,渗透转化思想[3].如此,在教师有目的、有意识的引导下,学生在日常学习中就能逐渐掌握常见的数学思想.

3.2 小组合作研讨,强化数学思维

为促进学生数学思维的发展,帮助其克服解题思维障碍,在日常解题训练中,还应给学生提供思考的时间和空间,引领学生以小组合作的方式,围绕数学问题进行研讨.通过小组的思维碰撞,在多个角度思考和探究问题的过程中,不仅加深了学生对数学问题的深度理解,也促进了数学思维的发展.

再如,已知等腰三角形的底和腰长分别是方程x2-6x+8=0的两个根,求等腰三角形的周长.这一数学问题学生在日常解题中常常出现漏解的现象.鉴于此,以此题为契机,引领学生开展研讨,使其在研讨的过程中明确“当底边为2、当底边为4”两种解题思路[4].如此,不仅避免了漏解的现象,也在研讨的过程中促进了思维的深刻性、广泛性和灵敏性.

3.3 一题多解,拓展解题思维

在初中数学解题中,为了促进数学思维的发展,积极开展一题多解训练十分必要.具体来说,一题多解就是聚焦同一题目,引领学生结合不同的数学知识,从不同的角度、不同的层次进行思考、分析,最终从不同的角度完成数学题目的解答.在这一过程中,学生在多角度、多层次的分析中,深刻发现数学的本质,并在多角度的探究中,提升数学思维的深刻性、敏捷性,真正拓展数学解题思维.

例如,如图1所示,已知正方形ABCD,E是BC边上的一点,且∠AEF=90°,EF与正方形外角平分线CF相交于点F,求证:AE=EF.

图1

针对这一几何问题,教师在培养学生数学思维时,就可采用“一题多解”训练,引领学生从不同的角度进行思考、分析,寻找多种解题方法.

方法一,构造全等三角形.如图2所示,在AB边上取一点G,使得AG=CE,连接EG.如此,构造出全等三角形,并结合题目已知条件,即可证明△AGE≌△ECF,进而得出AE=EF.

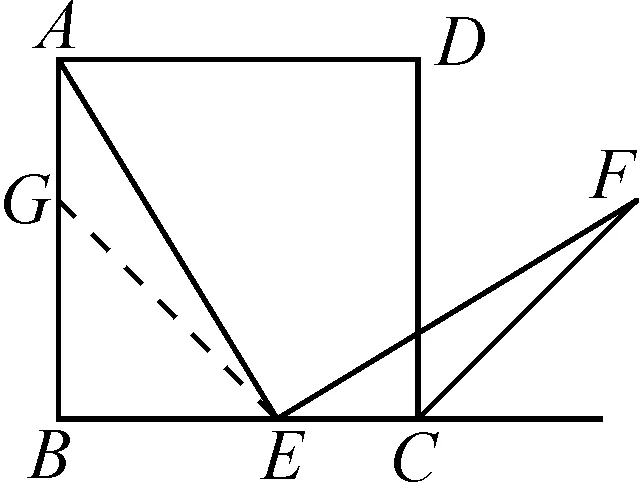
图2

方法二,构造等腰三角形.如图3所示,连接AC延长至点G,使得CG=CF,连接EG.如此,通过题中已知条件,先证明△ECF≌△ECG,得出∠F=∠G,∠FEC=∠GEC,EG=EF,并借助外角平分线性质,证明△EAG是等腰三角形,再由△ECF≌△ECG,得出AE=EF.

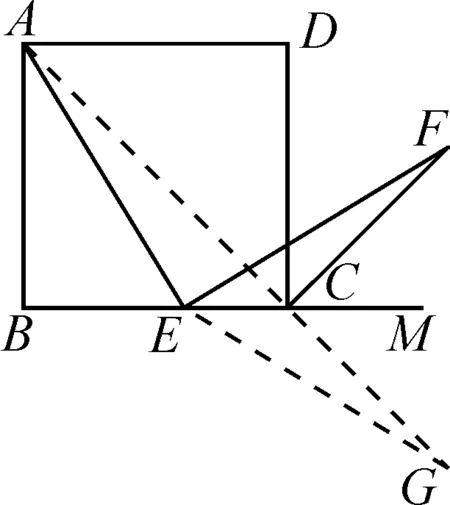
图3

方法三,构造平行四边形.如图4所示,延长AB至点G,使得BG=BE,连接EG,CG.容易证明△ABE≌△CBG,并得出EGCF为平行四边形,再通过AE=GC,EF=GC,证得AE=EF.

图4

如此,经过一题多解训练,学生在多角度的分析和探究中不仅理解了数学的本质问题,也在深度探究中促进了数学思维发展,极大地提升了数学解题能力.

3.4 变式训练,强化解题思维品质

为了强化初中生的数学解题思维,在日常解题教学中,还应结合相应的题目,积极开展变式训练,使得学生在“一题多变”的过程中,强化对数学知识的理解,并拓展数学解题思维,提升数学思维的广泛性和灵活性.例如,求不等式-5a>6的解.针对这一问题,为了强化学生的数学思维训练,可通过变换条件、问题、结论等方式,展开一系列的变式训练.

变式1如果x”“<”或“=”).

变式2如果axb,x应该满足______.

变式3求关于a的不等式(n+3)a>6.

变式4若关于a的不等式3na-2<3n-a的解集为a<2,求n的取值范围;

若关于a的不等式3na-2<3n-a的解集为a>2,求n的取值范围.

如此,学生在一系列的变式中,不仅完成了对题目的深度理解,也逐渐拓展了自身的数学思维[5].

4 结束语

综上所述,鉴于数学学科的特点,解决数学问题,对学生的数学思维水平提出了很高的要求.可以说,学生的思维水平和解题能力息息相关.鉴于此,教师在日常解题教学中,不仅要重视数学解题教学,还应立足学生在解题中面临的思维障碍,借助必要的解题思维训练,不断提升学生的数学思维品质,进而提升其数学解题能力.