周红永

⦿ 江苏徐州睢宁县桃园中学

新课标要求培养学生的创新精神与独立自主的学习能力.课标的落实,要以课本为载体.教学中以课本例题或练习题为基础,细解读,精加工,再重组,实现知识的有机统一,让学生在结构知识的引领下唤醒旧知识,引发新知识,从而促进学生的数学高阶思维能力发展.高阶思维是指发生在较高认知水平层次上的心智活动或认知能力,在认知过程分类中表现为分析、评价和创造.其中,分析指的是一种系统性思维,要求从整体上把握各部分的联系,从而理解事物的本质.因此,教学中要通过发现问题,并找出问题的症结,不断发展学生的高阶思维能力.笔者把平时的做法做了如下反思.

1 溯本求源,提高学生高阶思维能力

在八年级刚开始,学生对复杂图形的证明问题打不开思路,看图的视野仅局限于题目本意,缺乏联想思维,所以解题时总是无从下手,有时即使有切入点也显得没有条理.听了杨裕前教授的讲座《溯本求源 正本清源》,犹如醍醐灌顶.图形的识别要用运动的眼光去看,平移、旋转与翻折是图形变换的基础,所以教学中要学会溯本求源,寻找基本的图形运动,建立模型,利用转化思想找到思考的突破口,开阔学生解题的视野,帮助学生能站在更高的出发点去解题.

问题1(课本原题改编)如图1,若点A在线段BC上,△ABD,△AEC都是等边三角形,AD与BE相交于点G,AE与CD相交于点F.你能从条件出发,运用联想,通过独立思考把能直接或间接知道的量尽可能地在找出来吗?

图1

在学生解答问题1之前,先帮助学生梳理几个有价值的思考方向,引导如下:

(1)图2中有哪些相等的线段、相等的角?

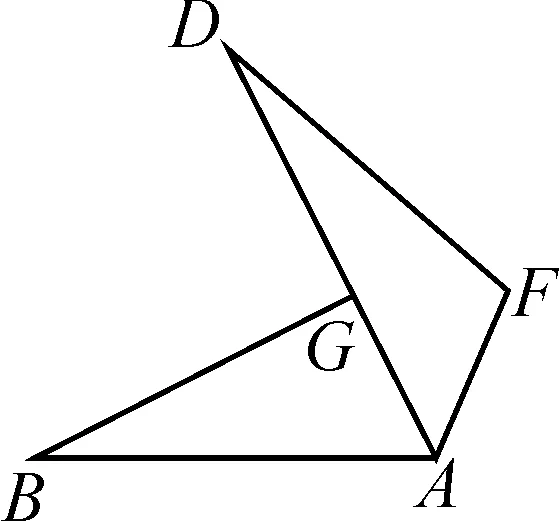
图2

(2)你还能间接推导出哪些角相等?

(3)谁看出图1中还有我们已经学习过的什么图形?(学生可以很快看出△BAE≌△DAC,如图3.) △BAE是怎样变化得到△DAC的?由全等三角形的性质你还可以得到什么?

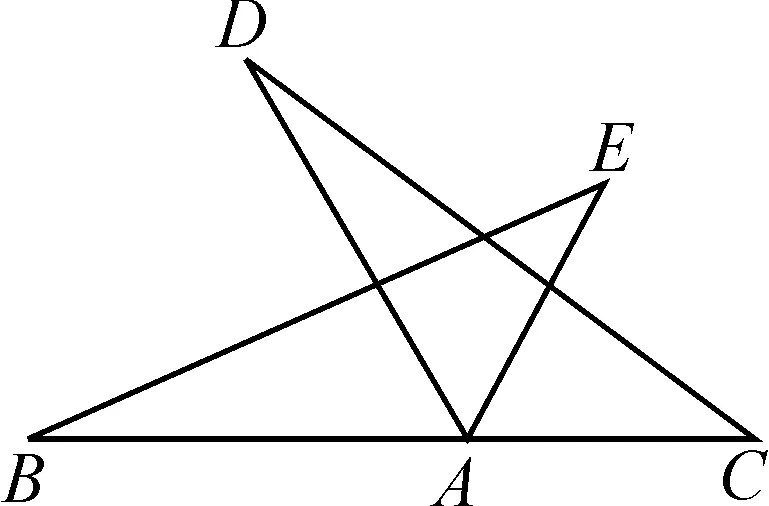
图3

(4)还有没有其他全等的三角形?

从最基本的线段和角入手,分解读图的难度.由∠BAE=∠DAC联想到角的和差关系,从而自然联想到最基本图形运动产生的全等模型.教材的例题、习题不断地强化从运动的角度认识全等,学生可以联想到△ABG≌△ADF,题目便很容易解决.

2 挖掘教材中可替代图形,通过迁移变化提高学生高阶思维能力

以问题为切入点,回归课本,挖掘教材中可替代图形,锻炼学生转化思想,培养发散思维和创新能力.利用变式训练来促进学生的思考,从而提高学生高阶思维的能力.

问题2(课本原题)如图4,在△ABC中,分别以AB,AC为边,向△ABC外作正三角形,BE,CD相交于点O.

图4

(1)试说明△ABE≌△ADC;

(2)探究:∠BOC=______.

变式1如图5,图6,在△ABC中,分别以AB,AC为边,向△ABC外作正四边形、正五边形,BE,CD相交于点O.试说明:①△ABE≌△ADC.②图5中,∠BOC=______;如图6,∠BOC=______.

图5

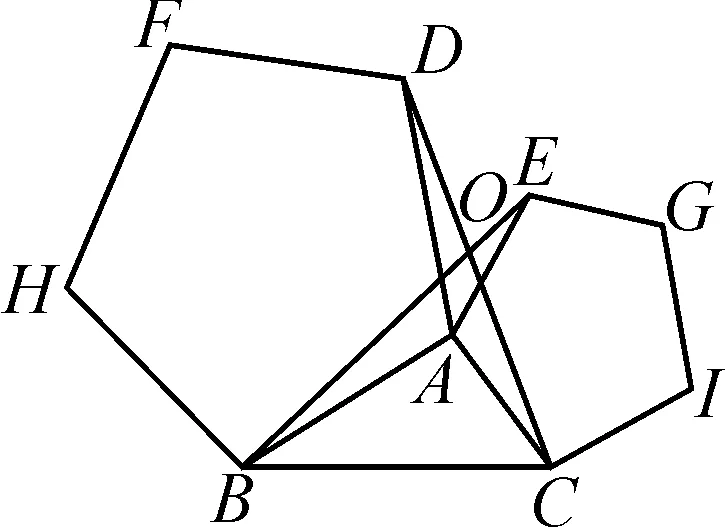
图6

如图7,如果AB,AD是以AB为边向△ABC外所作正n边形的一组邻边;AC,AE是以AC为边向△ABC外所作正n边形的一组邻边;BE,CD的延长相交于点O.试猜想:∠BOC=______(用含n的式子表示).

图7

这样基于课本原题的变式设计,使学生在变化中找寻不变性,灵活地运用知识,养成乐于思考的习惯,使思维的发展更进一步.

变式2等边三角形可以用等腰直角三角形或正方形来代替.

例1如图8,△ABD,△AEC都是等边三角形,求证:BE=DC.

图8

(由已知易证△ABE≌△ADC,得BE=DC.)

变式练习:(1)如图9,若△ABD,△AEC都是等腰直角三角形,∠ADB=∠AEC=90°,那么BE=DC吗?

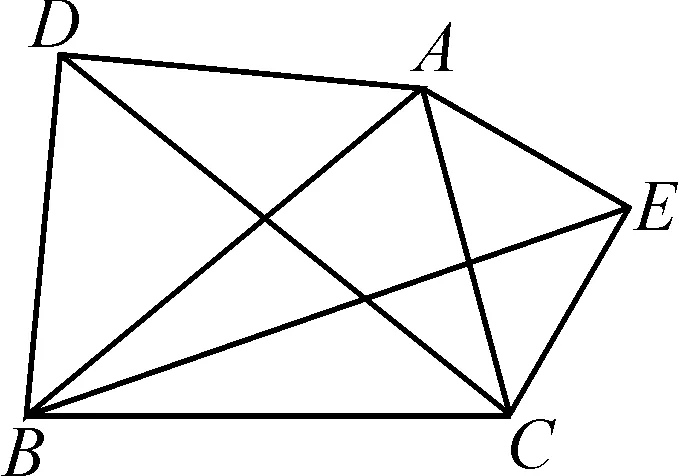
图9

(2)如图10,若四边形ABFD、四边形ACGE都是正方形,那么BE=DC还成立吗?求证BE⊥DC.

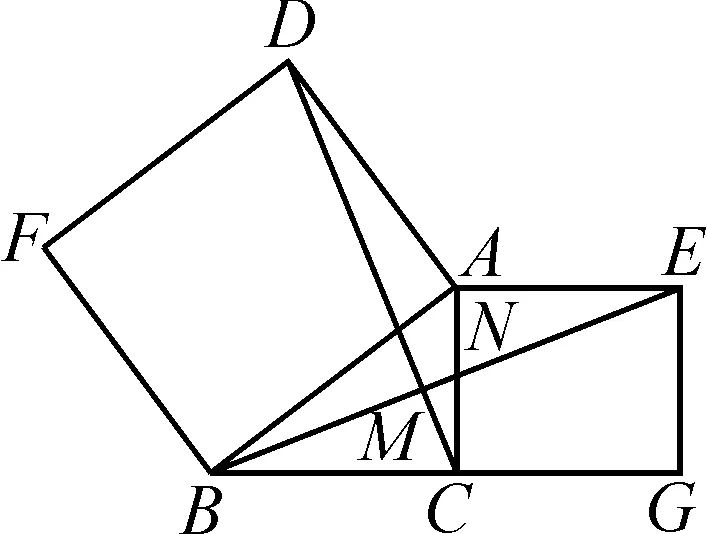
图10

(3)如图11,若点A在线段BC上,△ABD,△AEC都是等边三角形,那么BE=DC吗?若AD与BE交于点F,AE与CD交于点G,那么AF=AG吗?△AFG是等边三角形吗?为什么?

图11

3 架构知识网络,疏通知识的连接点,促进学生高阶思维的发展

在平时的教学中发现,很多时候学生的知识处于断点状态,解决问题时会出现不同程度的错误,于是,笔者以发现的问题为切入点,回归课本,从教材中寻找知识间的内在联系,帮助学生疏通知识的连接点,架构知识网格,从而促进高阶思维的发展.

通过本题,笔者发现学生已有的知识是碎片化的,缺乏系统性和连续性.笔者认为,要立足课本例题,搭建知识之间的桥梁,架构起完全平方式、一元二次方程根与系数的关系,以及根的判别式和二次函数图象与x轴交点个数之间纵横相连的关系,使知识富有整体性、连续性、系统性,在此基础上运用知识去解决问题,提高高阶思维能力.

例2若α,β是一元二次方程3x2+2x-9的两根,分别求下列各式的值:

立足课本习题,设计这样有层次性的题目,符合“人人都能获得良好的数学教育,不同的人在数学上得到不同的发展的要求”的新课程理念,促进高阶思维的发展.

苏霍姆林斯基在给《教师的建议》一书中“10 第一次学习新教材”认为:“学生学业落后,成绩不及格的根源之一,就是第一次学习新教材没有学好……知识是在不停地发展的,对某段教材的学习将持续一段长的时间,对知识的每一次运用,同时也是知识的发展和深入.而第一次学习新教材,是由不知到知、由不懂到理解事实、现象、性质、特征的实质而迈出的重要的第一步.” 所以,知识建构对于学生新知的理解运用有着举足轻重的作用.

4 把握知识的实质,把握思维的生长点,促进学生高阶思维的发展.

以问题为切入点,回归课本,反复揣摩知识的精髓,准确掌握知识的实质内容,精准把握学生思维的生长点,促进学生高阶思维的发展,以适用未来时代发展的要求.

问题4(课本原题)图12为某二次函数图象的一部分,有如下四个结论:

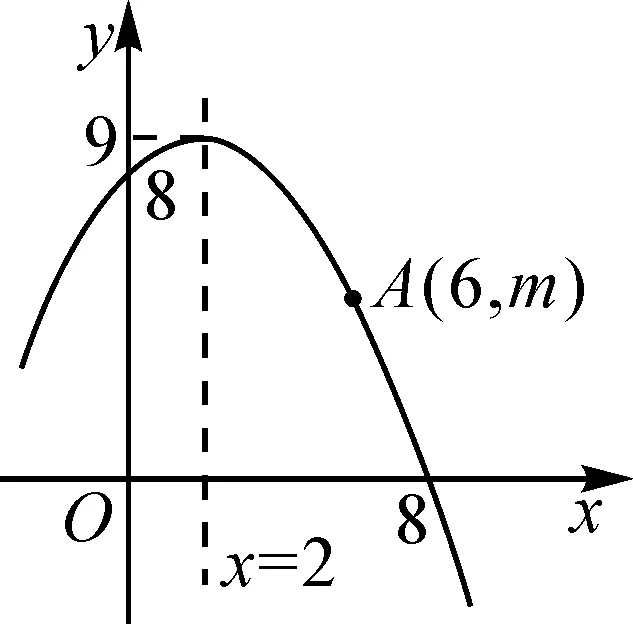
图12

②若B(-1,n)在这个二次函数图象上,则n>m;

③该二次函数图象与x轴的另一个交点为(-4,0);

④当0

正确结论的序号是( ).

A.①③ B.①④ C.②③ D.②④

学生解决本题时出现了很严重的错误,这是由学生不熟悉二次函数图象及性质、缺乏几何直观、运算能力和推理能力弱造成的.针对这个问题再次回归苏科版数学九年级下册第26页“学会‘读’二次函数的图象”一文,通过课本的再研读,学生忽然有种柳暗花明之感.

课本是浓香的醇酒,是教学的根基,要多品,细品,慢品,在回味中不停思考,总结,提高.Z