姚 军 李爱民

⦿ 江苏省高邮市甘垛镇澄阳初级中学 ⦿ 江苏省仪征市新集中学

中考试题的命制立意是体现考试目的,反映学科本质及课程教学改革方向.一份高质量的试卷是命题人经过反复推敲、仔细斟酌、精心打磨形成的,由科学、可信、新颖、有充足的信息和一定深度的考题组成.其中压轴题尤为突显,它综合性较强,一般从学生所学知识、思维方法、问题呈现等方面进行设计,突出考查学生数学学科的关键能力,体现培养学生学科素养和素养目标的整体结构能力.

当然,很多压轴题由于受时间、空间、难度要求等方面的限制,还有一些知识未能呈现在试题中,如果从设问的不同角度进一步挖掘定能展现更完整的知识体系,同时对学生的思维能力的培养起到延续和创新作用.笔者通过对2023年扬州市中考数学试卷第28题的深度探寻,挖掘了更多有价值的问题,以达到培养学生几何直观、空间观念、推理能力的目的,帮助学生感悟数学的价值,并能够从问题解决的过程中获得数学活动经验,对数学产生好奇心和求知欲,增强学习数学的兴趣,建立学习数学的信心[1].

1 原题呈现

在平面直角坐标系xOy中,已知点A在y轴正半轴上.

(1)如果四个点(0,0),(0,2),(1,1),(-1,1)中恰有三个点在二次函数y=ax2(a为常数,且a≠0)的图象上.

①a=______.

②如图1,已知菱形ABCD的顶点B,C,D在该二次函数的图象上,且AD垂直于y轴,求菱形的边长.

图1

③如图2,正方形ABCD的顶点B,D在该二次函数的图象上,点B,D在y轴的同侧,且点B在点D的左侧,设点B,D的横坐标分别为m,n,试探究n-m是否为定值,如果是,求出这个值;如果不是,请说明理由.

图2

(2)已知正方形ABCD的顶点B,D在二次函数y=ax2(a为常数,且a>0)的图象上,点B在点D的左侧,设点B,D的横坐标分别为m,n,直接写出m,n满足的等量关系式.

2 试题解析

上述试题解析如下.

解析：(1)①由于二次函数y=ax2顶点在原点,对称轴为y轴,因此可判断点(0,2)不在该二次函数的图象上,其他三个点在该二次函数的图象上,进而求出a=1.

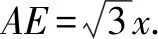
③如图3,若点B,D同在y轴右侧,过点B,D分别作y轴的垂线,垂足分别为M,N,易得△ABM≌△DAN,所以BM=AN,AM=DN.因为B(m,m2),D(n,n2),所以AN=m,AM=n,NO=n2,MO=m2.因为NO-MO=MN,所以n2-m2=m+n,即(n+m)(n-m)=m+n.又n+m≠0,所以n-m=1.若点B,D同在y轴左侧,同理可得n-m=1.综上可得,n-m=1.

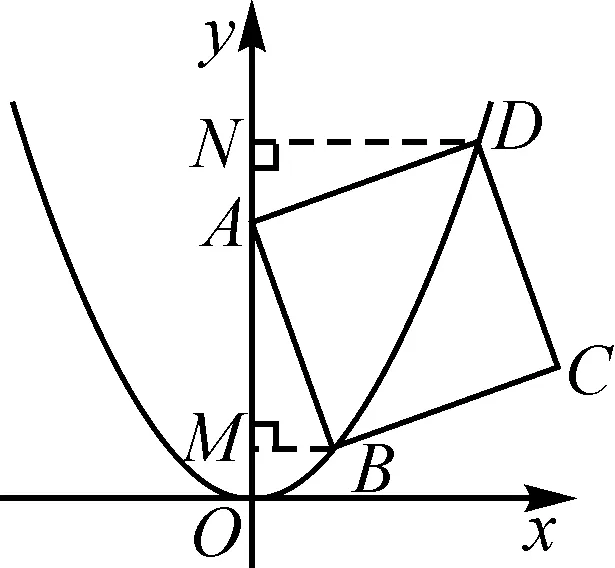
图3

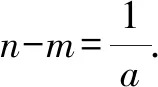
图4

评注：本题以探索图形在抛物线上的运动产生的几何模型为背景,关注学生的代数推理能力.综合考查二次函数与特殊四边形等初中数学核心知识,考查学生几何直观能力与图形模型思想.通过图形的运动变化,突出对模型思想、分类讨论、数形结合等数学思想方法的考查.作为综合题,问题层层推进,难度逐步增加,体现了从特殊到一般的数学思想,起到了区分与把关的作用.

3 考题再思考

3.1 对未关注的点A,C的思考

接着原题(1)中的第③问继续探究,在正方形ABCD中,我们关注的点当然是抛物线上的B,D两点,这两点始终在抛物线上,而另两点A,C往往被我们忽略了,其中点A在y轴正半轴上运动,它引领点B,D的位置,但运动的轨迹始终是一条射线.正方形ABCD中还有一点C,它的运动轨迹又是什么呢?

借助几何画板追踪点C,会发现点C的运动路径是一条抛物线,如图5.怎么理解呢?

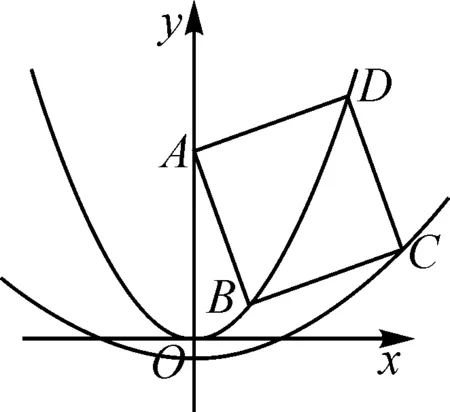
图5

如果把B,D两点看作一动点(两点位置存在一定的关系),点C随点B,D的运动而运动,又点B,D在抛物线上运动,由“瓜豆原理”可知点C也在抛物线上运动.

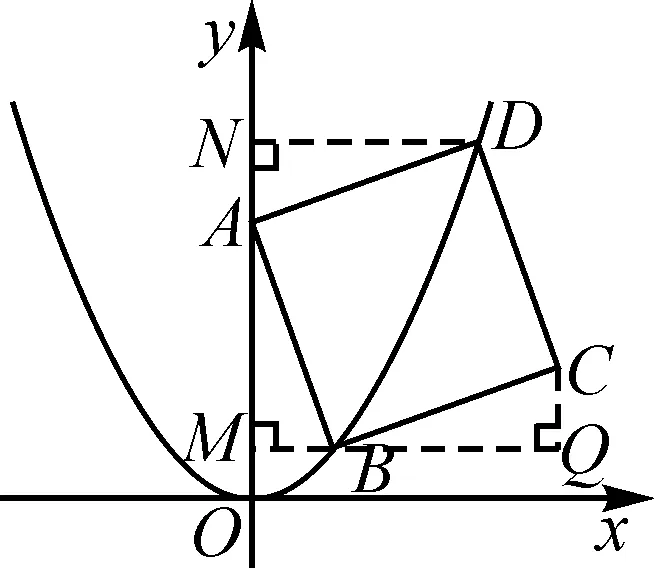
图6

基于此结论,可以设置如下问题:

(1)求动点C的轨迹方程;(2)求动点C的纵坐标的最小值;(3)求正方形ABCD面积的最小值.

在探寻点C的运动轨迹时,两次运用了“K”字型模型进行转化,一次是找B,D两点横坐标的关系,另一次是找点C与B,D两点横坐标的关系,对思维能力的要求较高.学生从中获取了解决问题的基本策略,同时培养了代数推理能力.

3.2 对抛物线的一般性思考

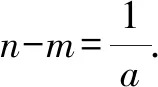
3.2.1 将抛物线沿y轴平移

将抛物线y=ax2(a为常数,且a>0)沿y轴向上或向下平移|k|个单位长度,此时抛物线的解析式为y=ax2+k(a为常数,且a>0).

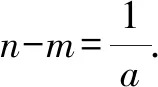
图7

3.2.2 将抛物线沿x轴平移

图8

3.2.3 将抛物线沿x轴、y轴平移

将抛物线y=ax2(a为常数,且a>0)的图象先沿x轴向左或向右平移|h|个单位长度,再沿y轴平向上或向下平移|k|个单位长度,此时抛物线的解析

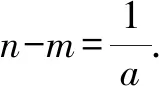
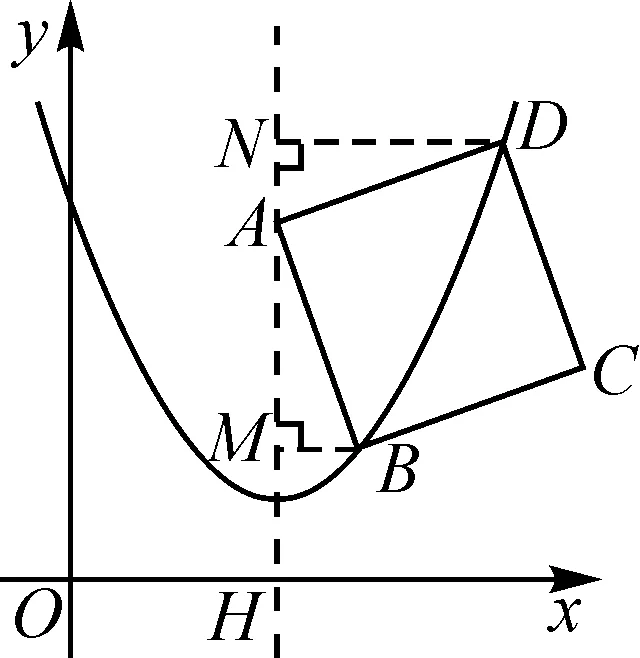
图9

不难发现,无论抛物线怎么平移,这样的正方形若存在,则B,D两点的横坐标的关系只取决于对称轴的位置以及a的大小.基于此结论,可以设置如下问题:对于二次函数y=ax2+bx+c(a,b,c为常数,且a>0),点A在对称轴上,正方形ABCD的顶点B,D在该二次函数的图象上,试探究B,D两点横坐标的关系.

在研究图形的性质和运动过程时,如果从整体变化和相对位置不变的角度探寻,进行纵向挖掘,层层推理,由易到难,会发现更深刻、更一般的结论.这样不仅可以优化考题设计,也能够促进数学思维的纵深拓展.

4 感悟反思

4.1 立足方法,形成解题模式

上述试题的探究立足于帮助学生构建这类数学问题的解题模式,促进学生对图形在抛物线上运动这一模型的识别和深度探寻,对学生提高解题速度和深度理解解题过程都有很大的帮助.该试题总结了与抛物线相关的正方形中B,D两点的横坐标之间的数量关系.上述探究都是通过设点的坐标,并用坐标表示线段的长度,再根据几何模型中线段的数量关系列出方程,进而推导出B,D两点的横坐标之间的数量关系.将解题经验显性化、一般化,并总结出其中蕴含的数形结合、化归与转化、方程、函数建模等数学思想方法.

4.2 知识生长,激发思维延续

开展考题探究不仅要关注解题突破过程,还应重视拓展过程,在拓展的过程中促进知识的生长.弗赖登塔尔认为“数学学习唯一正确的方法是让学生进行‘再创造’,也就是说,由学生本人把学习的东西实现或创造出来,教师的任务是为学生的发展创造条件、引导探索”[2].因此,平时的考题研究应不局限于原题,还应大胆探究,推广衍生新问题,这样学生的思维在原有的基础上又能得到延续和发展,从而促进学生深入思考问题,把问题真正想深、悟透、学活.

4.3 渗透素养,聚焦关键能力

考题是学科素养和关键能力落实的主要衡量指标之一,这就要求教师平时不能仅停留在对考题方法的研究上,还应对考题立意、本质、拓展加以探究,旨在把学生对考题“研”的过程转向教师对考题“命”的研究上.上述试题中,通过图形在抛物线中的运动所产生的数学问题,让学生在分析问题过程中借助数学模型培养几何直观、逻辑推理、数学运算等素养.

总之,在深度学习背景下的初中数学压轴题的探究中,教师应注重培养学生发现并提出问题、分析并解决问题的能力,提高学生的问题意识,最终通过巧妙的问题设计,不断提升问题厚度,使学生拓展思维宽度,提升思维深度,进而提升数学素养和关键能力.