李慧云,叶国菊,刘尉,赵大方

(1.河海大学理学院, 江苏 南京 210098;2.湖北师范大学数学与统计学院, 湖北 黄石 435000)

0 引言

由于实际问题环境多变以及人主观意识上的经验性和不精确性, 带有不确定性的优化问题, 如模糊优化问题, 区间值优化问题等引起了许多学者的研究,如文献[1-5].其中区间值优化问题是用区间数来表示不确定性, 这一形式的优化问题比起模糊优化问题限制较少, 因此具有广泛的应用性, 如赵大方[6]利用区间数研究了水质问题并进行了决策, 张建科[7]研究了区间数形式的优化问题以及鲁棒优化模型等.

在研究区间优化问题时, 区间值函数的导数及凸性是必不可少的.近年来也提出了许多关于区间值的导数的概念, 其中Wu[5]首次将区间值函数的弱导数概念应用于区间优化问题并得到最优性条件, 之后Antczak等[8]将文献[9]中的实值函数E-可微概念结合弱可微概念推广至区间值函数情况, 并得到E-KKT优化条件.而就凸性而言, 由于凸性条件较为严格, 在经济和控制领域等实际问题中很难满足, 因此出现了众多相关文献来研究那些和凸函数具有相似性质的更广义凸函数.比如在Wu[5,10]提出了区间值函数的LU-凸概念后,黎君等[11]、Zhang等[12]将区间值函数的LU-凸进一步推广至LU-预不变凸以及CW-不变凸, 使得该类广义凸区间值函数能够应用于更多实际问题.另外Zhang等[13]和Antczak[8]、Abdulaleem[14]将文献[15]中在放宽凸集和凸函数概念后所提出的E-凸函数类推广至区间值函数, 也在很多实际优化问题中得到了很好的应用.

受到文献[8]和[16]的启发, 笔者提出CW-E-对称可微区间值函数概念并研究其相关性质.基于该导数及其性质, 我们引入CW-序关系下的CW-E-预不变凸区间值函数及CW-E-对称不变凸区间值函数概念并探寻二者之间的关系; 最后借助CW-E-对称导数及广义不变凸区间值函数, 我们得到了广义不变凸区间值优化问题的E-最优性条件.

本研究内容按如下展开: 第一节回顾了基本概念并提出CW-E-预不变凸区间值函数概念, 第二节引入CW-E-对称可微区间值函数并介绍其相关性质, 进而研究CW-E-预不变凸区间值函数和CW-E-对称不变凸区间值函数的关系.第三节形成了非光滑广义凸区间值优化问题, 在映射E:Rn→Rn下, 得到了另一可微区间值优化问题.通过研究二者等价性, 证明了非光滑区间值优化问题的E-最优性条件, 并举例说明了我们结果的有效性.最后,第四节得到了本文中的结论.

1 预备知识

设R为实数集,对任意的aL,aU∈R,当aL≤aU时,称该闭区间[aL,aU]={x|x∈R,aL≤x≤aU}为一个区间数.本文中我们用I来表示所有闭区间数所组成的集族.显然,当aL=aU时,该区间数退化为实数.

对于任意的区间数A∈I都可用序对aL,aU来表示,其中aL,aU分别称为区间数A的左边界及右边界.此外,区间数还可用其中点和半径表示,即

A=[aL,aU]=

(1)

区间运算的基本规则具体如下:

任取I中的元素A,B,其中A=[aL,aU],B=[bL,bU],对任意k∈R有:

A+B=[aL,aU]+[bL,bU]=[aL+bL,aU+bU];

关于区间数的更多内容, 可参看文献[1,17].

在区间优化问题中,需要对所得的区间最优值进行比较,这涉及到对区间数进行排序的区间序关系.

设A=[aL,aU],B=[bL,bU]是两个闭区间,则ACWB当且仅当ac≤bc和aw≤bw同时成立;ACWB当且仅当ACWB且A≠B.

类似可定义LU-序关系, UC-序关系.

Wu[5]中给出区间值函数定义,称f:x∈Rn→I为一个区间值函数,若f(x)=[fL(x),fU(x)],其中对任意的x∈Rn成立fL(x)≤fU(x).与区间数类似,f可写为f(x)=.

为了用CW-序关系定义新的CW-E-预不变凸区间值函数和CW-E-对称不变凸区间值函数,并研究其相关性质,先回顾已有的E-不变凸集以及广义不变凸函数的概念.

定义1[15]设M⊂Rn,若存在向量函数η:Rn×Rn→Rn和E:Rn→Rn,对∀x,y∈M,∀λ∈[0,1]成立E(y)+λη(E(x),E(y))∈M,则称集合M为关于η的E-不变凸集.

定义2[14]设E:Rn→Rn,M⊂Rn为关于向量函数η:Rn×Rn→Rn的E-不变凸集, 且f是M上的E-可微实值函数.若对∀x,y∈M成立f(E(x))-f(E(y))≥η(E(x),E(y))T▽f(E(y)),则称f在M上为关于η的E-不变凸函数.

定义3[18]设E:Rn→Rn,M⊂Rn为关于向量函数η:Rn×Rn→Rn的E-不变凸集,f是M上的实值函数.若对∀x,y∈M,∀λ∈[0,1]成立f(E(y)+λη(E(x),E(y)))≤λf(E(x))+(1-λ)f(E(y)),则称f在M上为关于η的E-预不变凸函数.

在文献[13]中基于区间LU-序关系, 将实值函数的不变凸及预不变凸概念推广至区间值函数.本文中给出在CW-序关系下的CW-E-预不变凸区间值函数概念.

定义4设E:Rn→Rn,M⊂Rn为关于向量函数η:Rn×Rn→Rn的E-不变凸集,f是M上的区间值函数.称f在M上为关于η的CW-E-预不变凸函数,若对∀x,y∈M,∀λ∈[0,1]成立f(E(y)+λη(E(x),E(y)))CWλf(E(x))+(1-λ)f(E(y)).

定理1设E:Rn→Rn,M⊂Rn为关于向量函数η:Rn×Rn→Rn的E-不变凸集,f(x)=是M上的区间值函数.则f在M上为关于η的CW-E-预不变凸区间值函数当且仅当fc和fw在M上都是关于同一个η的E-预不变凸实值函数.

定理1的证明由CW-序关系和定义4, 易证充分性成立; 由CW-序关系和定义3可得必要性成立.

2 CW-E-对称可微区间值函数及其相关性质

本节给出了一类E-对称可微实值函数和CW-E-对称可微区间值函数的概念并研究其相关性质.在这之前,先回顾已有的可微函数的概念.

定义5[20]设f:X⊂Rn→R为实值函数.称f在x0∈X处对称可微,若存在fs(x0)使得‖h‖→0时,有θ(x0,h)∈R→0,且

f(x0+h)-f(x0-h)=2fs(x0)h+θ(x0,h)‖h‖.

定义6[24]设x0∈X⊂Rn和h∈Rn.如果如下式极限存在

那么f在x0处沿方向h的对称方向导数存在.

定理2[24]设h∈Rn,如果实值函数f在x0∈X处对称可微,那么Dsf(x:h)存在且成立

Dsf(x:h)=fs(x)Th.

定义7[9]设E:Rn→Rn,f:Rn→R是一个定义在Rn上的实值函数(不必要可微).则f在x0∈Rn处是E-可微的当且仅当f∘E在x0处可微(通常意义下的可微),也就是存在▽s(f∘E)(x0)∈Rn,θ(x0,·):Rn→R,使对于充分小的h∈R,有

(f∘E)(x0+h)=(f∘E)(x0)+▽(f∘E)(x0)h+θ(x0,h)‖h‖,

其中当‖h‖→0时有θ(x0,h)→0.

梁波等[16]指出, 如下函数在x0=0处对称导数不存在, 即:

受此启发, 提出E-对称可微实值函数类.

定义8设E:Rn→Rn,称不必要可微实值函数f:Rn→R在x0∈Rn处E-对称可微, 若实值函数f∘E在x0处对称可微,即存在▽s(f∘E)(x0)∈Rn,θ(x0,·):Rn→R,使当‖h‖→0时有θ(x0,h)→0,且

(f∘E)(x0+h)=(f∘E)(x0-h)+2▽s(f∘E)(x0)h+θ(x0,h)‖h‖.

此外,文献[8]中将E-可微实值函数概念成功推广至区间值函数,因此本研究也自然地提出区间值函数CW-E-对称可微性定义.

定义9设E:Rn→Rn,称一个区间值函数f=:Rn→I在x0∈Rn处CW-E-对称可微,如果实值函数(fc∘E)和(fw∘E)是对称可微实值函数.

接下来先给出E-对称可微下E-对称不变凸实值函数概念和CW-E-对称不变凸区间值函数概念, 进而给出区间值函数在CW-E-对称可微下,CW-E-对称不变凸性与CW-E-预不变凸性间的关系.

定义10设开集M⊂Rn,E:Rn→Rn,η:Rn×Rn→Rn,称E-对称可微实值函数f:M→R为关于η的E-对称不变凸函数, 如果∀x,y∈M成立

f(E(x))-f(E(y))≥η(E(x),E(y))T▽sf(E(y)).

文献[11-12]中分别根据区间LU-序关系和CW-序关系, 给出区间值不变凸函数概念.基于此,本文中同样将实值E-对称不变凸函数推广至区间值函数情况.

定义11设E:Rn→Rn,M⊂Rn为关于向量函数η:Rn×Rn→Rn的E-不变凸集,f=是M上的区间值函数.若实值函数fc和fw在M上关于同一个η是E-对称不变凸的, 则称f在M上为关于η的CW-E-对称不变凸区间值函数.

在给出CW-E-预不变凸区间值函数与CW-E-对称不变凸区间值函数的关系前, 我们先证明一个引理.

引理1设实值函数f在M上E-对称可微, 并假设f的右侧方向导数D+f(x:h)存在,就有Dsf(x:h)存在.若存在一个由正实数形成的序列{tn}使得当n→∞时有tn→0,且∀x,y∈M成立

f(E(y)+tnη(E(x),E(y)))≤tnf(E(x))+(1-tn)f(E(y))

(2)

则f在M上是E-对称不变凸函数.

f(E(x))-f(E(y))≥η(E(x),E(y))T▽sf(E(y)),

引理得证.

命题1设M⊂Rn为关于η:Rn×Rn→Rn的E-不变凸集, 若f在M上是关于η的CW-E-预不变凸连续E-对称可微区间值函数且设fc∘E,fw∘E右侧方向导数存在就有对称导数存在, 则f在M上也是关于同一个η的CW-E-对称不变凸区间值函数.

命题1的证明因为f在M上是关于η的CW-E-预不变凸连续E-对称可微区间值函数,则由定理1和定义9可知, 实值函数fc和fw在M上都是关于同一个η的E-对称可微E-预不变凸函数, 再由引理1和定义11可知结论成立.

注1命题1的逆不成立, 下面例子进行说明.

例1设M=(0,1],f(x)=[1,5]ex,η(x,y)=-1,E(x)=x, 则fc(x)=3ex,fw(x)=2ex均为E-对称不变凸函数, 但不是关于同一个η的CW-E-预不变凸区间值函数.

命题2设M⊂Rn为关于η:Rn×Rn→Rn的E-不变凸集,f在M上是关于η的E-对称可微区间值函数.若f在x*∈M处是CW-E-对称不变凸的,则对∀0<ξ,μ∈R,ξfc+μfw在x*处也是关于同一个η的E-对称不变凸实值函数.

命题2的证明因为f在M上是关于η的E-对称可微区间值函数且在x*∈M处是CW-E-对称不变凸的, 由定义11和定义9可知,fc,fw在x*处关于同一个η是E-对称可微不变凸实值函数.由定义10可得对x,x*∈M, 成立

fc(E(x))-fc(E(x*))≥ηT(E(x),E(x*))▽sfc(E(x*))

和

fw(E(x))-fw(E(x*))≥ηT(E(x),E(x*))▽sfw(E(x*)).

对非负数0<ξ,μ∈R,我们得到

ξfc(E(x))-ξfc(E(x*))≥ηT(E(x),E(x*))▽sξfc(E(x*))

(3)

和

μfw(E(x))-μfw(E(x*))≥ηT(E(x),E(x*))▽sμfw(E(x*))

(4)

由(3)和(4)式可得,对x,x*∈M成立

[ξfc(E(x))+μfw(E(x))]-[ξfc(E(x*))+μfw(E(x*))]≥ηT(E(x),

E(x*))▽s[ξfc(E(x*))+μfw(E(x*))],

因此ξfc+μfw在x*处也是关于同一个η的E-对称不变凸实值函数.

3 广义不变凸区间值优化问题的最优性条件

本节考虑如下区间值优化问题IVOP:

minf(x)=

subject toX*={x|gi(x)≤0,i∈I={1,2,…,m}},

其中f:Rn→I为区间值函数(不必要可微),gi:Rn→R是实值函数,X*为优化问题IVOP的可行解集合.

Wu在文献[5]中给出关于区间值优化的LU-最优解概念,[21]也给出这一类区间值优化问题的CW-最优解.

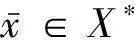
在本文始终假设IVOP中区间值函数f和实值函数gi分别是CW-E-对称可微和E-对称可微的, 且E既是单射也是满射.

为了得到CW-E-对称可微区间值优化问题IVOP的最优性条件, 我们建立如下另一区间值优化问题IVOPE, 并说明二者之间的联系.

min(f∘E)(x)=<(fc∘E)(x),(fw∘E)(x)>

subject toXE*={x|(gi∘E)(x)≤0,i∈I={1,2,…,m}}

我们称IVOPE为E-区间值优化问题,XE*为优化问题IVOPE的可行解集.

现在, 我们讨论问题IVOP和IVOPE解之间的关系.

类似于文献[8,引理3.5]和[13,引理2～4], 可证明如下3个结论.

引理2设E:Rn→Rn既是单射又是满射, 若XE*={x:(gi∘E)(x)≤0,i∈I},则E(XE*)=X*.

引理3设E:Rn→Rn既是单射又是满射, 且x*∈X*是IVOP的CW-最优解,那么存在t*∈XE*使得E(t*)=x*,且t*是IVOPE的CW-最优解.

引理4设E:Rn→Rn既是单射又是满射, 若t*∈XE*是IVOPE的CW-最优解, 则E(t*)是IVOP的CW-最优解.

从上述引理, 我们可得到关于优化问题IVOP的CW-E-最优解的概念.

为了证明优化问题IVOP的CW-E-最优解的E-KKT必要条件, 首先引入E-KT约束品性和Motzkin’s 定理.

定义14[8](E-KT约束品性)设E:Rn→Rn以及t*∈XE*是给定的.假设gi,i∈I在t*处是E-对称可微的,如果对任何满足▽s(gi∘E)(t*)Td≤0,∀i∈I(E(t*))={i∈I:(gi∘E)(t*)=0}的d∈Rn,d≠0,都存在一个在0 处右可微的函数φ:[0,1]→Rn和实数τ>0使得

(5)

则称在t*处满足E-KT约束品性.

定理3[23]给定m×n矩阵A及l×n矩阵C≠0,以下两个系统有且只有一个有解: 系统1,Ax≤0,Cx>0,x∈Rn; 系统2,ATκ=CTλ,κ∈Rm,λ∈Rl,κ,λ≥0,λ≠0.

接下来给出区间值优化问题IVOP的最优性条件.

定理4(E-KKT必要条件)设E:Rn→Rn既是单射又是满射,t*∈XE*是IVOPE一个可行解.假设区间值函数f在t*处关于η是连续CW-E-对称可微的.设U(t*,)为t*的邻域,且设关于▽s(fc∘E)(t*),▽s(fr∘E)(t*)的对称导数存在,gi,i∈I在t*处关于同一个η是连续E-对称可微实值函数.若t*是IVOPE的CW-最优解且在t*处满足E-KT约束品性, 则存在Lagrange乘子(ξ,μ)∈R2,ξ≥0,μ≥0,不全为0,0≤ζi∈R,i∈I,成立

ii)ζi(gi∘E)(t*)=0,i=1,2,…m.

定理4的证明我们需要证明不存在d∈Rn,d≠0使得以下式子成立:

▽s(fc∘E)(t*)d<0,▽s(fw∘E)(t*)d<0;▽s(gi∘E)(t*)d≤0

(6)

不妨先假设存在d∈Rn,d≠0使得式(6)成立.那么由假设,E-KT约束品性在t*处成立, 因此存在函数φ:[0,1]→Rn在0处右可微以及实数τ>0使得式(5)成立.另外由f在t*处关于η是连续CW-E-对称可微的,由定义9可知,实值函数fc∘E,fw∘E在t*处是关于同一个η的连续对称可微函数,则由文献[16,定理9],存在t1,t2及t3,t4使得fc∘E,fw∘E成立:

(fc∘E)(t*)+▽s(fc∘E)(t*)T(φ(α)-t*)+‖φ(α)-t*‖θc(t1,φ(α)-t*)

≤(fc∘E)(φ(α))

≤(fc∘E)(t*)+▽s(fc∘E)(t*)T(φ(α)-t*)+‖φ(α)-t*‖θc(t2,φ(α)-t*)

(7)

和

(fw∘E)(t*)+▽s(fw∘E)(t*)T(φ(α)-t*)+‖φ(α)-t*‖θw(t3,φ(α)-t*)

≤(fw∘E)(φ(α))≤(fw∘E)(t*)+▽s(fw∘E)(t*)T(φ(α)-t*)

+‖φ(α)-t*‖θw(t4,φ(α)-t*)

(8)

其中,φ(α)∈U(t*,)且当‖φ(α)-t*‖→0时,θc(tk,φ(α)-t*)→0,θw(tk,φ(α)-t*)→0,k∈{1,2,3,4}.

将此代入式(7)～(8),得

+‖φ(α)-t*‖θc(t2,φ(α)-t*)

(9)

和

+‖φ(α)-t*‖θw(t4,φ(α)-t*)

(10)

因此,由α>0,τ>0及当‖φ(α)-t*‖→0时,有θc(tk,φ(α)-t*)→0,θw(tk,φ(α)-t*)→0,k∈{2,4}可知, 如下不等式成立

(11)

这与t*是IVOPE的CW-最优解矛盾.这就意味着不存在d∈Rn满足式(6).

因此,由定理3可知,令矩阵CT=(-▽s(fc∘E)(t*),-▽s(fr∘E)(t*))及AT=(▽(g1∘E)(t*),…,▽(gi∘E)(t*)),i∈I(E(t*)),那么存在Lagrange乘子(ξ,μ)∈R2,ξ≥0,μ≥0,不全为0,0≤ζi,i∈I(E(t*)),成立

若设ζi=0,i∈II(E(t*)),那么结论得证.

定理5(E-KKT充分条件)设E:Rn→Rn既是单射又是满射,t*∈XE*是IVOPE的一个可行解.假设区间值函数f在t*处关于η是CW-E-预不变凸且CW-E-对称可微的,gi,i∈I在t*处关于同一个η是E-对称可微且E-对称不变凸函数.若存在Lagrange乘子(ξ,μ)∈R2,ξ≥0,μ≥0,不全为0,0≤ζi∈R,i∈I,成立

ii)ζi(gi∘E)(t*)=0,i=1,2,…m.

那么t*是IVOPE的CW-最优解,E(t*)是优化问题IVOP的CW-E-最优解.

再由CW-序关系的定义可得:

(12)

又因为f在t*处关于η是CW-E-预不变凸和CW-E对称可微的, 由定义9可知, 实值函数fc∘E,fw∘E在t*处是关于同一个η的对称可微函数, 再由命题1可知,fc,fw在t*处是关于同一个η的E-对称不变凸函数, 从而由ξ≥0,μ≥0,不全为0及式(12)则有

(13)

(14)

将式(13)和(14)相加可得

这与定理5条件i)矛盾.因此t*是IVOPE的CW-最优解,由引理4和定义13知E(t*)是优化问题IVOP的CW-E-最优解,得证.

例2设

(15)

考虑如下非可微向量优化问题(IVOP1)

minf(x)

subject tog1(x)=-x≤0,

g2(x)=x-1≤0.

我们可得

(16)

以及

(17)

从而当取

4 结论

本文中重点提出区间值函数的CW-E-对称导数以及引入两个新的广义不变凸函数, 即CW-E-预不变凸区间值函数和CW-E-对称不变凸区间值函数.本研究所提出的导数比文献[8]中的E-导数及文献[20]中的对称导数更广泛.另外, 我们通过使用本文中提出的CW-E-对称导数及广义不变凸区间值函数概念, 得到了非光滑非凸的区间值优化问题的E-最优性条件.最后的例子也说明了本文中结果的有效性.但是由于考虑的优化问题中的约束函数仍是实值函数, 因此未来可考虑约束函数为区间值函数的优化问题及用本文中所提出的CW-E-对称导数来研究区间优化问题的对偶问题.