基于PISA2021分析高考情境题的数学推理能力
2022-03-07俞卓君周莹陈基河
俞卓君 周莹 陈基河








【摘要】本文以PISA2021数学推理与问题解决为框架,从情境、内容、素养、过程四个维度,结合部分高考情境试题说明数学推理的具体体现,以期为教师教学提供参考.研究结果表明近几年高考数学卷情境化试题背景在函数、几何、概率等主线都有所体现,并贯穿于六大核心素養中.为了更好地培养学生的数学推理能力,在教学中可以注重对解释部分的评价,同时加强数学抽象与数学建模素养的培养,情境试题的素材选取更多贴近生活实际.
【关键词】PISA2021;数学推理;问题解决;高考情境试题
1问题提出
PISA是一项跨国跨文化的指向学生素养评估的大规模测试,无论是试题还是测评结果都对教育评价有着重要的研究意义.PISA2021测评框架与前几个版本的区别是重点强调了数学推理能力在问题解决过程中的体现\[1\],如图1.
PISA测试与中国的数学高考测试内容完全不同,但都希望能在检测过程中反映社会需求\[2\].高速发展的21世纪对培养多样化高素质人才、发展高阶思维的需求愈加紧迫,\[34\]问题解决成为发展高阶思维、培养21世纪技能的重要途径.许多国家都把发展学生的数学推理能力放在问题解决过程中培养,并成为了重要的教学目标之一.推理能力在问题信息的提取、筛选和整理过程中起着至关重要的作用,更是帮助作出恰当判断和决策的重要思维能力\[5\].
PISA2021强调将对数学推理的理解置于现实世界的真实情境,数学情境问题解决需要学生多种核心素养在情境中共同作用,是一种较高水平的数学素养.\[67\]李娜等学者分析了PISA2021测试框架,提出可以结合具体的数学内容来说明数学推理的具体体现\[1\].PISA2021给出了理解数学推理的六个关键:理解数量、数系及其代数性质;感知抽象和符号表征的力量;意识数学结构和它们的规则;认识数量之间的函数关系;借助数学模型作为观察现实世界的镜头;理解方差是统计的核心\[8\].
为了深入探究数学推理在情境试题中的实际应用,本文参考PISA2021数学素养重点关注的数学推理能力与问题解决相互联系的框架,以近年来部分高考数学情境类试题为研究对象,将抽象的推理能力具体化,期望能够为数学问题解决过程中培养学生的数学推理能力提供参考.
2分析维度
本文分别从情境维度、考察的内容维度、情境中的素养维度以及问题解决的过程维度来分析高考试题中体现出来的数学推理能力,由于PISA2021中提出了理解数学推理能力的六个关键点,因此本文分析的高考样题分别根据六个关键点进行选取.
2.1情境维度
本文主要关注高考试题中的4类情境:一是个人情境,个人情境与个人生活息息相关,包括旅行、购物等;二是社会情境,社会情境与学生身边环境相关,比如人口数量、经济政策等;三是职业情境,职业情境大多涉及财务成本、质量控制等;四是科学情境,包括气象、医药、遗传、环境等.
2.2内容维度
PISA2021的数学素养框架中将数学内容分成了四类:数量、不确定性与数据、变化与关系、空间与图形.由于分析样题来自于高考试题,因此本文选取的内容维度以课程标准为依据,结合高中数学三大主线:函数、几何、概率与统计进行阐述.
2.3情境中的核心素养维度
《普通高中数学课程标准(2017年版)》提出了6种数学核心素养:数学抽象、直观想象、数学建模、逻辑推理、数学运算、数据分析.每一道情境问题的解决都涉及多个核心素养,这也是数学推理能力在多素养中的体现.
2.4问题解决的过程维度
PISA2021将数学推理能力在问题解决的过程分成三方面:数学推理的表达、数学推理的应用、数学推理的解释\[8\].学生在“表达”过程中提取问题的关键信息,在“应用”过程中解决问题,在“解释”部分能结合实际阐述答案与结论.三个过程具体包括的活动如表1所示[1].
3试题分析
3.1理解数量、数系及其代数性质
在高中阶段,学生需要掌握几种重要的运算对象:数、字母(代数式)、向量等\[11\].数字是数学的中心概念,学生对情境问题进行数学推理的前提是能够正确理解数字体系及对应的数量关系.中学数学包括多种数字表示形式,这需要学生能够在多种形式之间进行转化,如建立简单代数等式、绘制图形、建模,并在数字的转化应用中进行运算.
例1(2019年全国卷理科17题)
为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到P(C)的估计值为0.70.
(Ⅰ)求乙离子残留百分比直方图中a,b的值;
(Ⅱ)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
本题情境为科学情境(小白鼠医学实验),在医学实验运用科学技术手段进行药物检测的过程中,常常通过对小白鼠的试验数据来分析检测某种药物的含量、有效性等关键信息.在内容维度上,本题主要考查频率分布直方图及概率的运算.主要考查了数学运算和数据分析的核心素养.学生通过概率估计值与事件C描述的运算过程,感悟其中蕴含的逻辑推理.
数学推理的过程体现在:要求确定数学变量“事件估计值”和“平均值”在直方图中的含义,能够识别问题隐含的数学关系,根据P(C)的估计值列出对应关系式.在应用中要能够进行基本的数学运算,根据运算结果得到数学结论.本题要求学生解释直方图中呈现的信息,这一部分的解释体现在学生的思维中,求出甲乙各自的平均值后,学生能够根据均值的含义认识两种溶液的集中趋势.
3.2感知抽象和符号表征的力量
数学是一门研究数量关系与空间形式的学科,具有高度的抽象性和形式化的特点.在中学数学中,抽象是从问题情境中提取具体对象、运用符号表征进行数学运算等思维活动的过程.
例2(2021年上海卷19題)
已知某企业2021年第一季度的营业额为1.1亿元,以后每个季度的营业额比上个季度增加0.05亿元,该企业第一季度的利润为0.16亿元,以后每季度比前一季度增长4%.
(1)求2021年起前20季度营业额的总和;
(2)请问哪一季度的利润首次超过该季度营业额的18%?
本题情境属于社会情境(企业利润变动),企业的营业额与利润分析能够反映该企业的经营状况,从而帮助财务部门根据分析结果对未来的营销决策做出预测.在内容上,这道题主要考查函数的单调性,运用数学抽象与逻辑推理使用函数解决问题.过程中涉及符号语言和文字语言,文字语言用于描述情境问题,符号语言用于表征数学概念和原理.数学推理的过程体现在:学生应该使用合适的变量、符号来数学化地描述问题情境.在本题中,文字语言为:首次超过该季度营业额的18%,符号语言为:0.16×(1+4%)n>(1.1+0.05n)×18%.在题中要创建恰当的数学解决策略,如第一问要求学生能构建以1.1为首项,0.05为公差的等差数列.在解释上,有了计算结果则可根据提问说明对应的实际结论.
3.3意识数学结构和它们的规则
数学结构是各种数学对象的统称,在解题中往往起着支撑作用,解题者可以通过对结构的感知、识别、联想、归纳、类比、转化等方式实现解题目标\[13\].在数学结构观下,对结构的另一种重要的处理方式是合情推理\[14\],学生首先认识到问题情境的结构,判断关键的结构要素,通过归纳类比的方式了解结构,再将结构应用到问题情境中.
例3(2019年理科全国卷Ⅱ16题)
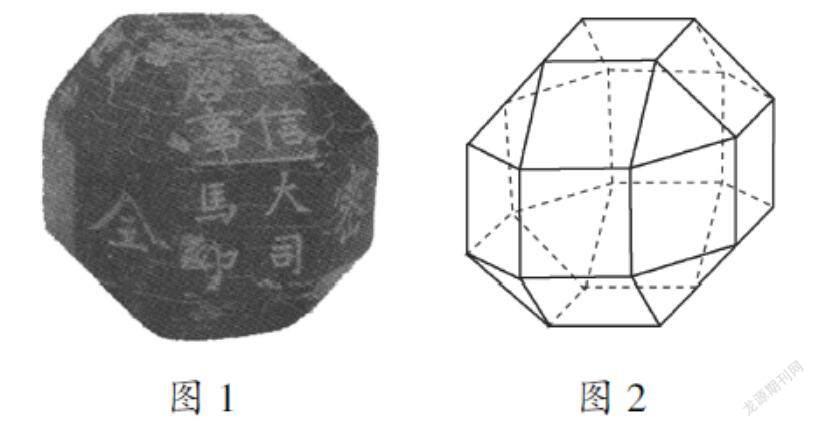
中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有个面,其棱长为.
本题情境为科学情境(中国金石文化),以中国文化为载体,以半正多面体为对象,主要考查正方体的结构以及棱长的概念,考查了直观想象和数学抽象的核心素养.本题借助学生已有认知结构中的空间几何体模型作为认识世界的工具,对于不认识的几何体,能否通过观察它的特殊结构并联想到已经学过的知识,得到未知事物的特性. 数学推理的过程体现在:学生要能够使用合适的图形来数学化地呈现情境问题.金石是一种不规则形状,但根据题目提示可将其抽象在正方体中.将图2与正方体的结构搭建联系,这一步有助于学生能够准确认识两者的形态位置,有了对图2更加立体的观察、比较,才能够推断并分析出二者棱长的位置关系.根据抽象出来的图,可以推导出半正多面体棱长x与正方体棱长1的关系式为: 22x+22x+x=1,抽象的过程即为解释图形信息的过程.
3.4认识数量之间的函数关系
变量之间相互依赖和相互作用会对问题情境产生影响,从而影响学生的数学推理能力.数量之间的函数关系蕴含在问题情境中,可以选择多种方式对其表示,如方程式、图表、表格或文字描述.学生解决问题除了关注题目中确定的量,也要考虑可变的量,以及变量之间的变化规律,比如具有某种线性关系的函数.
在问题解决中,函数有着双重属性,既可以作为过程,也可以作为对象.作为过程的函数在数学表征中是抽象的,要将其作为对象,需要学生通过数量关系将其具体化.
例4(2020年理科全国新高考卷6题)
基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:I(t)=ert描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足R0=1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln2≈0.69)().
A.1.2天B.1.8天
C.2.5天D.3.5天
本题情境为科学情境(新冠肺炎疫情时间变化).突如其来的新冠肺炎疫情在全球范围内大流行,疫情的传播程度和严重性令人深感担忧的同时,各国医药专家通过计算机等科技手段对疫情的传播速度和感染人数进行研究,在调取了大量现实数据的基础上估计模型.在内容维度上,这道题主要考查指数函数模型的实际应用.指数函数是高中重要的基本函数模型之一,解答本题的关键步骤是能够建立两个时间——病例数增加前(t1)与增加后(t2)的两个关系式.同时本题考查了数学运算和逻辑推理的核心素养.数学推理的过程体现在:对于抽象的数学表述,学生也可以借助指数函数的图象表征形式来翻译时间变化的过程,通过图象更直观、立体地感受该模型变化的动态性和过程性.本题建立在疫情大数据的背景下,学生要能够处理数据信息、代数表达式I(t)=ert,并根据问题建立方程.
3.5借助数学模型作为观察现实世界的镜头
模型是对现实的简化,数学模型可以使学生将学习的数学知识与现实世界存在的问题情境建立科学联系.数学模型是用数学语言来表述的,以图象或者函数关系式的形式,突出某一情境中的某些因素.
在一般情况下使用数学模型,通常能够进行数据的分析和评估(模型是否适合数据),对未来做出预测,得到研究结果,并根据结果评估模型的充分性和准确性.在模型的建立与使用中引导学生关注情境中最重要的元素,将复杂的问题归结为某种数学本质,进而帮助学生利用模型进行数学推理.
例5(2021年北京卷8题)
对24小时内降水在平地上的积水厚度(mm)进行如下定义:
小明用一个圆锥形容器接了24小时的雨水,如图3,则这一天的降水量属于哪个等级().
A.小雨B.中雨C.大雨D.暴雨
本题情境为科学情境(气象预测模拟),在地理气象预测中,常常利用数学和信息技术对天气现象进行模拟分析以及预测,传统气象站的雨量器一般为圆筒,图3筒内含两节装置,上节为漏斗,下节为储水瓶.在内容维度上,这道题主要考查几何主线中圆锥体积的计算,考查了数学抽象、数学建模的核心素养.该问题的核心是圆锥体积V与厚度h(mm)之间的关系.数学推理的过程体现在:要求学生能够识别雨量器(圆锥体)是情境中模拟的数学模型,该模型对现实的气象预测进行了简化,学生要转换不同的数学语言对模型进行描述,从图象到数字再到文字,从而帮助做出预测.选择题的题型对学生的数学结果准确性要求较高,不仅要求学生能够创建合适的计算策略,也要求学生能够根据运算答案以及表格对应的信息得到对应结果,从而能够判断这种方法在实际生活中的合理性.
3.6理解方差是统计的核心
现实生活充满着不确定性,这种不确定性在21世纪的大数据背景下显得尤为突出,在统计学中,方差可以刻画随机变量的离散程度,我们需要认识到数据具有的偏离程度,对离散程度进行描述,进而对现实情境进行判断.
例6(2021年全国卷文科数学乙卷17题)
某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了 10 件产品,得到各件产品该项指标数据如下:
旧设备和新设备生产产品的该项指标的样本平均数分别记为和,样本方差分别记为 s21和 s22.
(1) 求, ,s21,s22;
(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高 (如果-≥2s21+s222 ,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).
本题情境为社会情境(设备质量控制).随着机器使用时间加长,陈旧会带来精度下降,但是否使用新设备,何时使用新设备也影响着工厂的成本,因此在实际生活中,通过新旧设备的测试指标进行统计,能够帮助工厂做出决策.在内容维度上,这道题主要考查均值与方差公式的计算,重点考查了数学运算与数据分析的核心素养.在高中阶段,数据分析的一个重要过程是整理数据,整理数据是有效进行数据分析的基础.数学推理的过程体现在:本题直接考查均值与方差的概念,要求学生能够写出计算,,s21,s22的步骤.学生应能够进行简单的数据运算,能根据题目条件判断计算结果.
4结论与思考
通过对近几年高考部分情境试题数学推理能力体现的分析可以看出,数学推理不仅仅存在于某个知识板块,而是囊括了函数、几何、概率多个板块.
在对情境问题进行数学抽象的过程中,为了将最终的结果指向数学问题的解决,需要以符号语言为工具进行推理.直观强调可视化,想象则需要根据学生的个体数学经验对直观图形进行判断,用数学语言描述直观想象的结构过程中体现数学推理能力.数学建模的目的是促进现实世界与数学知识的联系,帮助对现实问题做出合理推断和估计.数学运算属于数学中程序性知识的范畴,程序性知识需要按照规则与逻辑关系进行学习,因而在数学运算中能够潜移默化地渗透数学推理能力.学生在真实情境中进行数据分析时,不仅要在收集数据时需要根据某些条件判断数据的合理性与真实性,也要运用统计方法对数据蕴含的信息进行整理推断,在数据的认识与分析过程中发展数学推理能力.
基于研究结论,本文提出几点建议:
4.1课堂教学关注对数学推理的解释与评价
数学推理在问题解决中的过程包括表达、应用与解释,对数学推理的解释与评价要求学生能够结合问题的实际生活背景来阐述数学答案及其意义,这一过程鲜少能够体现在考试答卷上.因此在日常教学过程中,可以结合PISA 2021所给出的数学解释的具体信息(表1),帮助学生对问题解决中的数学推理进行归纳总结,解释推理不仅能培养创造性思维,也能使学生在问题解决中经历的过程更加完整.
4.2加强数学建模与数学抽象能力
数学推理能力与核心素养紧密关联,在现实情境中,数学抽象与数学建模对发展数学推理能力尤为重要.数学建模是用数学概念、原理和思维方法描述现实世界中具有数学规律性的事件.问题情境与数学建模和数学抽象息息相关,情境常常通过文字或者图形语言的模型来描述,提高抽象与建模的数学能力有助于学生在情境问题中发展数学推理能力.
4.3试题情境与时俱进,紧密联系生活实际.
PISA对于数学素养的测评试题往往来自真实情境,强调学生对具体的问题情境做出数学分析、推断和数学解释.数学问题情境种类繁多,涉及面广,或贴近生活或与大环境相关.例如在2020年新冠肺炎全球蔓延的环境下,学生亲历疫情人数暴增的阶段,也常通过新闻媒体报道感染病例数与治愈人数等真实事件来感受疫情数据的变化情况.学生虽然不能直接参与医学专家研制药品、制定模型等事件,但在未来职业中可能会从事相关实际问题.在設置真实情境中的数学问题时,需要考虑真实情境的语言描述,对数据进行取舍,考虑学生的认知水平.
参考文献
[1]李娜,赵京波,曹一鸣. 基于PISA2021数学素养的数学推理与问题解决\[J\]. 课程·教材·教法,2020,040(004):131137.
[2]任子朝,佟威,陈昂.高考数学与PISA数学考试目标与考查效果对比研究\[J\].全球教育展望,2014,43(04):3844.
[3]周莹,莫倩华,肖宝莹.美国大学招录标准评介及启示\[J\].数学教育学报,2019,28(06):4246.
[4]周莹,林毅.初中生数学高阶思维的结构模型建构及问卷编制\[J\].数学通报,2021,60(02):1624.
[5]吴宏.推理能力表现:要素、水平与评价指标\[J\].教育研究与实验,2014(01):4751.
[6]熊露,赵思林,程雪莲. 情境视角下2019年高考数学试题评析及教学建议\[J\]. 教学月刊·中学版(教学参考),2019,000(012):6165.
[7]邓海英,严卿,魏亚楠.数学情境问题解决错误分析与评价\[J\].数学教育学报,2021,30(01):6167.
[8]OECD. PISA 2021 mathematics framework(draft)\[R\]. Paris: OECD Publishing,2018:14.
[9]桑贾伊·马汉贾恩\[美\],兹比格涅夫·马齐尼亚克波兰,比尔·斯密特美,等. 2021年PISA数学——来自CCR的分析\[J\]. 数字教育,2019,005(005):P.8392.
[10]史宁中. 试论数学推理过程的逻辑性——兼论什么是有逻辑的推理\[J\]. 数学教育学报,2016,025(004):116,46.
[11]中华人民共和国教育部. 普通高中数学课程标准(2017年版)\[M\].北京:人民教育出版社,2018:47.
[12]谭业静,平光宇. 基于数学文化和核心素养的符号语言教学\[J\]. 基础教育论坛,2020(28).
[13]张宏斌. 试述数学结构思想及其在数学教学中的运用\[J\]. 辽宁教育行政学院学报,2006(12):125125.
[14]沈良. 略谈数学结构观下的解题与教学\[J\]. 数学通讯,2012(12):13.
[15]胡典顺,雷沛瑶,刘婷. 数学核心素养的测评:基于PISA测评框架与试题设计的视角\[J\]. 教育测量与评价,2018,213(10):4147+65.
[16]史宁中. 漫谈数学的基本思想\[J\]. 数学教育学报,2011.
作者简介俞卓君(1996—),女,广西南宁人,广西师范大学数学与统计学院在读硕士研究生;主要研究数学课程与教学论.
周莹(1962—),女,浙江嵊州人,廣西师范大学数学与统计学院教授,硕士生导师,特拉华大学访问学者;主要研究数学课程与教学论和教师教育.
陈基河(1996—),男,广西玉林人,广西师范大学数学与统计学院在读硕士研究生;主要研究数学课程与教学论.
