高广花， 汤 锐， 杨 倩

(南京邮电大学 理学院，江苏 南京 210023)

分数阶偏微分方程是指包含未知函数分数阶偏导数的方程.天文学[1]、金融学[2]、医药学[3]、物理学[4]等诸多领域中的许多数学模型都可以用分数阶偏微分方程描述.相较于整数阶偏微分方程，分数阶偏微分方程在模拟某些物理以及化学过程中的精确性更高，所以分数阶偏微分方程的理论研究及应用正成为备受关注的热点问题之一.分数阶导数有许多不同的定义，如Riemann-Liouville导数、Riesz导数、Caputo导数等.一般来说，时间分数阶导数用Caputo导数描述，而空间分数阶导数用Riemann-Liouville导数或Riesz导数定义.然而，大多数分数阶微分方程的解析解很难给出，尤其是变系数和非线性情形.因此，对分数阶微分方程寻找有效的数值模拟方法成为当前研究的重要课题之一.

目前，对于空间四阶时间分数阶扩散方程，已有诸多学者进行了研究.Jafari[5]等利用Adomian分解法得到了定义在有界空间域上的空间四阶分数阶扩散波方程的解.Hu和Zhang[6]利用降阶法研究了空间四阶分数阶扩散波方程的紧致差分格式，并证明了该格式的稳定性和收敛性.结合降阶法，通过定义平均值算子，Ji等[7]给出了一种处理第一类Dirichlet边界条件的方法.Vong和Wang[8]通过定义平均算子和离散的四阶差商算子，直接离散空间四阶导数，建立了求解第一类Dirichlet边界下空间四阶时间分数阶慢扩散方程的高阶紧致差分格式.Yao和Wang[9]考虑了Neumann边界下求解空间四阶时间分数阶慢扩散方程的有限差分方法.对于第一类Dirichlet边界下的空间四阶时间分数阶慢扩散方程，Cui[10]构造了一种紧致Stephson差分格式进行离散，将未知函数及其一阶导函数同时作为未知量耦合求解，但是所得格式的理论分析较为复杂.文献[11]使用样条法求解一类空间四阶时间分数阶偏微分方程.Xu等[12]提出了求解一类具有弱奇性核的空间四阶时间分数阶微积分方程的数值算法，然后采用离散能量法、Cholesky分解法和降阶法证明了该算法的稳定性和收敛性.

上述成果多是对单项时间分数阶问题进行的研究.然而，某些现象仅用单项分数阶方程描述是不够的，许多过程需要借助多项时间分数阶偏微分方程来描述，如具有损耗的物理过程[13]、黏弹阻尼现象[14]、氧气通过毛细血管输送到组织的过程[15]、在多种复杂黏弹性材料中发生的介质不规则扩散现象[16]等.特别是，多项时间分数阶扩散波方程可以有效地描述连续时间随机游动模型中的幂律频率依赖性[17].

查阅文献可知关于多项时间分数阶方程已有不少研究.Jin等[16]基于Galerkin有限元方法，对含有多个Caputo分数阶导数的时间分数阶扩散波方程建立了一种简单的数值格式.Gao等[18]在超收敛点处构造了逼近多项Caputo分数阶导数线性组合的数值公式，并证明了该公式至少可以达到二阶精度.Gao和Liu[19]采用降阶法对第二类Dirichlet边界下的空间四阶时间多项分数阶波方程建立了一种空间紧致差分格式，其中时间分数阶导数利用L1公式进行了逼近.Abdel-Rehim等[20]分别对时间分数波方程、剪切波方程、阻尼波方程的近似解进行了仿真,用G-L公式离散了Caputo时间分数阶导数，并讨论了这些数值方法的Von-Neumann稳定性条件.Wei[21]构造了求解一类多项时间分数阶扩散方程的全离散局部间断的Galerkin方法，并证明了该方法的无条件稳定性和收敛性.利用降阶法，Sun等[22]在超收敛点处建立了求解时间多项分数阶波方程的两种差分格式，并证明了格式的唯一可解性、稳定性和收敛性.Zhang等[23]考虑了多项时间分数阶Burgers流体模型，采用分离变量法得到了解析解，然后基于时间加权位移Grünwald差分算子和空间Legendre谱方法建立了数值方法，并提出了一种改进格式以提高收敛精度.

以上问题都是通过常数阶分数阶微分方程来描述的.然而，近年来，越来越多的学者发现，各种重要的动力学行为表现出变阶分数阶行为.这些分数阶行为可能随时间、空间或其他条件而变化，这表明变阶分数阶微积分是描述复杂问题的一种有效的数学工具.变阶分数阶导数是常数阶分数阶导数的推广，后者无法表征的一些现象，如扩散过程在多孔介质中的演化，外场随时间的变化等，都可以通过变阶分数阶导数进行描述.Samko和Ross[24—25]早在1993年和1995年就率先提出了变阶Riemann-Liouville和Marchaud分数阶微积分及它们的一些基本属性.Lorenzo和Hartley[26—27]总结了变阶算子的概念，其中变阶算子可随时间或空间变化.此外，他们对变阶积分和微分的概念，以及数学概念与物理过程之间的关系进行了深入研究.在此基础上，他们还进一步讨论了变阶分数阶微分模型的一些新的推广.Coimbra[28]在考虑分数阶导数的拉普拉斯变换的基础上，给出了变阶微分算子的一个新的定义.Ingman等[29—30]采用时间变阶算子对黏弹性变形过程进行了建模.Pedro等[31]利用变阶微积分研究了悬浮在带有阻力的黏性流体中的颗粒的运动.Du等[32]提出了求解多维变阶时间分数阶慢扩散方程的两种差分格式.二者均具有时间二阶精度，在空间上分别具有二阶和四阶精度.Wei和Yang[33]提出了求解一类时间变阶分数阶扩散问题的一种数值方法，时间方向用有限差分方法进行了离散，空间方向采用局部间断的 Galerkin方法进行逼近，并通过理论分析和数值算例证明了该方法的高精度.文献[34]基于位移二进制块区间划分和多项式近似，建立了求解变阶时间分数阶扩散方程的快速紧致差分格式，并从理论上证明了格式的无条件稳定性和收敛性.Ganji等[35]考虑了一类非线性的变阶微积分方程.Tian等[36]提出了一种求解时间多项变阶分数阶偏微分方程的无网格配置方法.

注意到，Ji等[7]建立了求解第一类Dirichlet边界下空间四阶时间分数阶方程的数值格式，但是该工作在边界点处引入了对空间二阶导数四点处加权平均的逼近，且只研究了单项时间常数阶问题.Cui[10]以空间一阶导数作为中间变量，建立了求解第一类Dirichlet边界下的空间四阶时间常数阶分数阶慢扩散方程的有限差分格式，但是其理论分析极具挑战性.Du等[32]考虑了求解空间二阶时间单项变阶分数阶慢扩散方程的有限差分方法，但是对于时间多项变阶分数阶问题没有进行相关研究.Tian等[36]考虑了求解时间多项变阶分数阶方程，但仅考虑了空间二阶问题，且未对所提算法进行理论分析.本文中，我们考虑空间四阶时间多项变阶分数阶问题.通过对边界条件进行巧妙处理，建立了求解第一类Dirichlet边界条件下空间四阶时间多项变阶分数阶慢扩散方程的高阶稳定的数值格式，并用离散能量分析方法证明了所得格式的稳定性和收敛性.主要贡献包括:

(ⅰ)在超收敛点处构造了逼近时间多项变阶分数阶导数线性组合的数值公式，并证明了该公式至少可以达到时间二阶精度.

(ⅱ)对边界进行巧妙处理.本文中在边界点处只引入了对空间二阶导数两点处加权平均的逼近，与文献[7]相比，算法更为简洁.应用降阶法，将空间二阶导数作为中间变量，并用离散能量分析方法对所建立的数值格式进行了稳定性和收敛性分析.与文献[10]相比，本文的理论分析更为直观易行.

1 预备知识

考虑如下第一类Dirichlet边界下时间多项变阶分数阶慢扩散方程：

f(x,t),x∈(0,L),t∈(0,T],

(1)

u(0,t)=g1(t),u(L,t)=g2(t),t∈(0,T],

(2)

ux(0,t)=γ1(t),ux(L,t)=γ2(t),t∈(0,T],

(3)

u(x,0)=φ(x),x∈[0,L],

(4)

假设u∈C3[t0,tn],1≤n≤N.记(L2,ku)(s)为函数u基于(tk-1,u(tk-1)),(tk,u(tk))和(tk+1,u(tk+1))3点插值得到的二次多项式，则有

且

(5)

余项为

u(s)-(L2,ku)(s)=

s∈[tk-1,tk+1],ξk∈(tk-1,tk+1),

1≤k≤n-1,1≤n≤N.

(6)

在区间[tn-1,tn]上，利用(tn-1,u(tn-1))和(tn,u(tn))两点对函数u做线性插值，记为(L1,nu)(s)，则

且

此外，有

(8)

定义

σ>0,n≥1.

引理2设m≥1， 由

注1引理1和引理2的证明可参考文献[18]和文献[32]得出，此处从略.

定理1设n≥1，u∈C3[t0,tn]，记

则

|rn|≤

证明易知

由

(tn-1+σn-s)-αr(tn-1+σn)-1ds]=

(tn-1+σn-s)-αr(tn-1+σn)-1ds

及

得到

(tn-1+σn-t0)-αr(tn-1+σn)]≤

对于(10)式中的第二项，由(8)式可得

(tn-1+σn-s)-αr(tn-1+σn)ds.

(12)

注意到Fn(σn)=0，从而

因此

(tn-1+σn-s)-αr(tn-1+σn)ds.

进一步可得

将(11)式和(13)式代入(10)式，即得(9)式. 定理证毕.

根据(5)式和(7)式可将数值微分公式改写为

[(k+1+σn)2-α(tn-1+σn)-2(k+σn)2-α(tn-1+σn)+

2(k+σn)1-α(tn-1+σn)+(k-1+σn)1-α(tn-1+σn)],

1≤k≤n-2,

(n-2+σn)2-α(tn-1+σn)]-

(n-2+σn)2-α(tn-1+σn)].

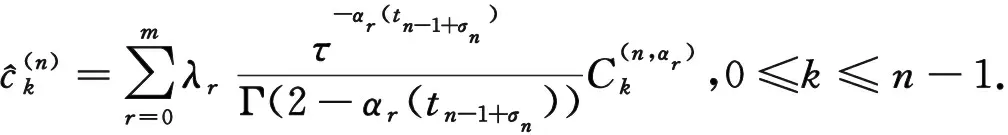
引理3[37]记θ(s)=(1-s)3[10-3(1-s)2],ξ(s)=(1-s)3[5-3(1-s)2].

(ⅰ)若函数g∈C6[x0,x1]，则有

(ⅱ)若函数g∈C6[xM-1,xM]，则有

(ⅲ)若函数g∈C6[xi-1,xi+1]，则有

下列引理给出了函数u(t)在t=tn-1+σn处的值的一个二阶逼近公式.

引理4[9]若u∈C3[tn-1,tn],σn满足0<σn<1，则

u(tn-1+σn)=σnu(tn)+(1-σn)u(tn-1)+O(τ2).

2 差分格式的建立

对任意网格函数u∈Uh，引入如下记号：

算子H通常被称为平均值算子或紧算子.

引入中间变量v(x,t)=uxx(x,t)，则方程(1)～(4)可等价写成

f(x,t),x∈(0,L),t∈(0,T],

(18)

v(x,t)=uxx(x,t),x∈(0,L],t∈(0,T],

(19)

u(0,t)=g1(t),u(L,t)=g2(t),t∈(0,T],

(20)

ux(0,t)=γ1(t),ux(L,t)=γ2(t),t∈(0,T],

(21)

u(x,0)=φ(x),x∈[0,L].

(22)

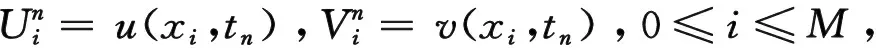
分别在点(xi,tn-1+σn)和(xi,tn)处考虑方程(18)～(19)，得到

vxx(xi,tn-1+σn)+qu(xi,tn-1+σn)=

f(xi,tn-1+σn), 0≤i≤M,1≤n≤N,

(23)

v(xi,tn)=uxx(xi,tn), 0≤i≤M,0≤n≤N.

(24)

对(23)～(24)式的两端同时作用算子H可得

Hvxx(xi,tn-1+σn)+qHu(xi,tn-1+σn)=

Hf(xi,tn-1+σn)，1≤i≤M-1， 1≤n≤N，

(25)

Hv(xi,tn)=Huxx(xi,tn),0≤i≤M,0≤n≤N.

(26)

根据引理3、引理4和定理1，可得

1≤i≤M-1,1≤n≤N,

(27)

(28)

其中存在正常数c1，满足

(29)

(30)

在方程(1)中，令x→0+，并注意到边界条件(2)，可得

(31)

方程(1)两端同时关于x求偏导一次，再令x→0+，并注意到边界条件(3)，可得

0≤n≤N.

(32)

同理，令x→L-，可以得出类似的2个方程.

当i=0时，(26)式为Hv(x0,tn)=Huxx(x0,tn),0≤n≤N,由引理3中(15)式及(31)～(32)式可得

其中

并且存在一个正常数c2,使得

(34)

同理可得

(35)

其中

并且存在一个正常数c3,使得

(36)

注意到初边值条件(20)和(22)，可得

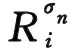
定理2差分格式(39)～(44)等价于

(45)

2≤i≤M-2,1≤n≤N,

(46)

1≤n≤N,

(47)

且

(50)

其中pn-1+σn=σnp(tn)+(1-σn)p(tn-1),qn-1+σn类似定义.

证明仿照文献[37]中定理3.1的证明易得，此处从略.

3 差分格式的稳定性和收敛性

先给出3个引理.

引理5[37]对任意网格函数v∈Uh，有

引理7[18]对任意网格函数un∈Uh,0≤n≤N，uσn=σnun+(1-σn)un-1，有

1≤n≤N.

对于单项变阶问题，文献[32]已有结果. 然而对于多项变阶问题，条件一非负性易得，条件二的证明不再显而易见. 但是参考对多项常数阶问题[18]和单项变阶问题[32]的研究技巧，条件二的证明亦可得出，此处从略.

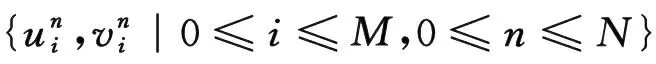
则有

(59)

证明由(54)式易得

由Cauchy-Schwarz不等式可得

1≤n≤N,

(62)

1≤n≤N.

(63)

将(62)～(63)式代入(61)式，整理得

1≤n≤N.

(64)

将引理5、引理6及引理7应用到(64)式，可得

由(55)～(56)式易得

从而有

改写(67)式可得

注意到

进一步可得

1≤n≤N.

递推可得

注意到(57)式并应用引理5，即可证明(59)式．定理证毕．

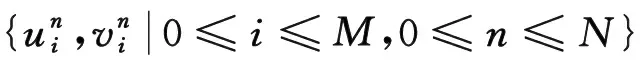
其中

证明将(27)～(28)式、(33)式、(35)式以及(37)～(38)式分别与(39)～(44)式对应相减，可得误差方程组为

1≤i≤M-1,1≤n≤N,

对上述误差方程组应用定理3，可得

将上式两边开方即得定理结果.定理4证毕．

4 数值实验

本节旨在应用一些数值算例验证本工作中所得算法的计算效果及数值精度. 记

-πt4-sin 1.该问题的精确解为u(x,t)=t4sin(πx)+cosx.

选取不同的λr和αr(t)(r=0,1,…,m)，应用差分格式(45)～(49)计算该问题．首先，取固定且足够小的空间步长h，时间步长τ从1/10细化到1/160，记录最大计算误差及收敛阶. 由表1可知，差分格式(45)～(49)在时间方向能达到二阶收敛，计算结果与理论分析吻合．

类似地，表2列出了空间步长h取不同值时的最大误差及收敛阶．由表2可知，差分格式(45)～(49)的空间方向收敛阶可达到理论上的四阶，与预期结果相同．

5 结论

本文在超收敛点处建立了逼近时间多项变阶Caputo分数阶导数线性组合的数值微分公式，并研究了所得微分公式的数值精度.首先，通过求解非线性方程，在每个时间层上找到了一个特殊的点，使得所得数值微分公式逼近时间多项变阶Caputo分数阶导数的线性组合在该点的值至少可以达到二阶精度. 其次，利用该数值微分公式求解第一类Dirichlet边界下空间四阶时间多项变阶分数阶慢扩散方程，建立了有效的差分格式，并利用能量分析法证明了所得格式的稳定性和收敛性. 数值算例证明了所得格式的有效性及理论结果的正确性.

另外，本文仅讨论了第一类Dirichlet边界下空间四阶时间多项变阶分数阶慢扩散方程的差分方法，很容易推广到求解第二类Dirichlet边界下空间四阶时间多项变阶分数阶慢扩散方程的初边值问题，此处不再赘述.

表1 M=100时差分格式(45)～(49)的数值误差及时间方向收敛阶

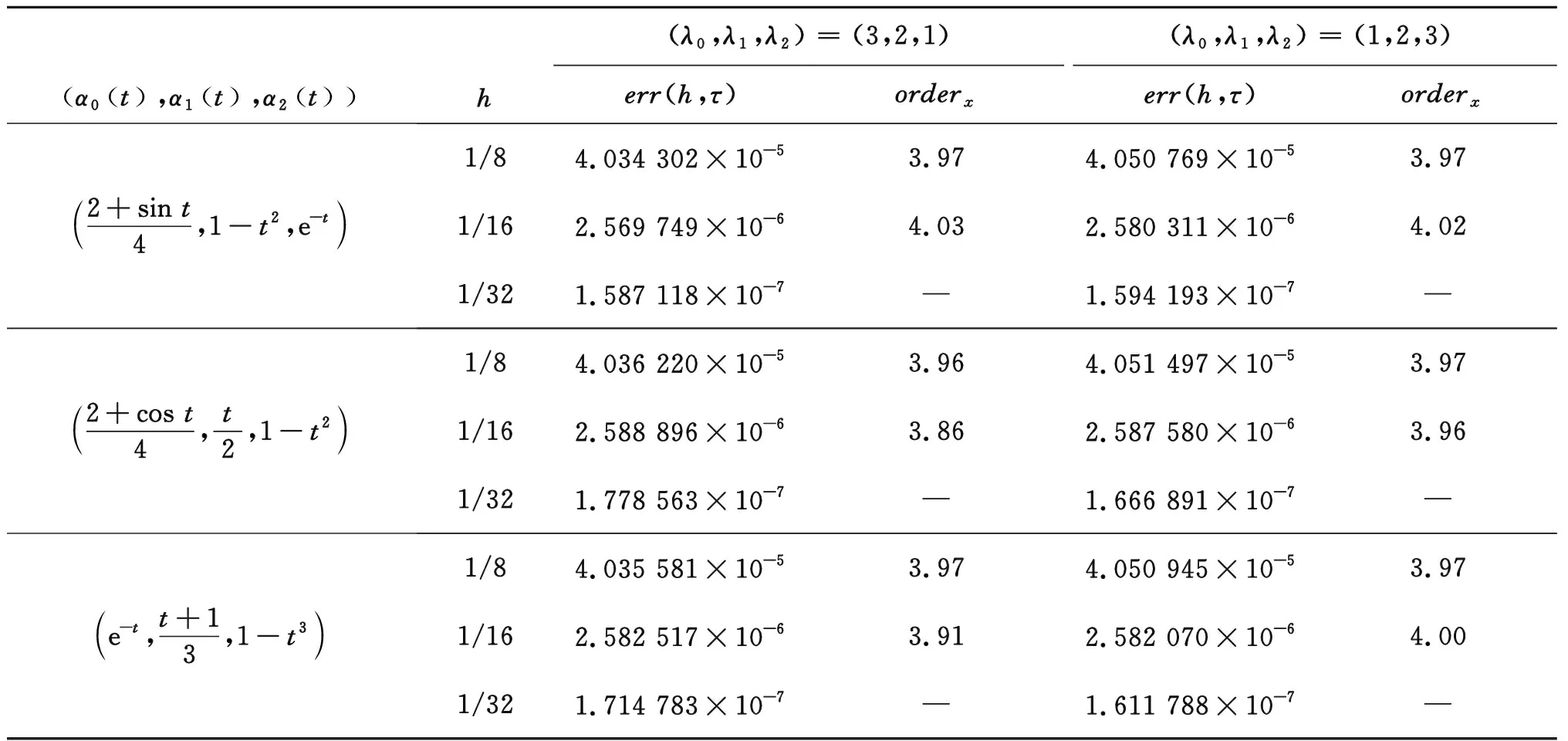
表2 N=10 000时差分格式(45)～(49)的数值误差及空间方向收敛阶