江苏省扬中中学 (212200) 张红玉

含有多元变量求最值问题，在各类考试中经常出现，由于变量太多，常有混淆视听、难以下手的感觉，本文通过举例分析，介绍五种常用的解题方法，供读者朋友参考．

一、适当配凑

例1 若a、b、c>0，且a2+ab+ac+bc=4，则2a+b+c的最小值为．

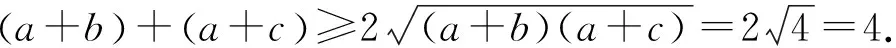
点评：本题中从表面上看不能直接运用基本不等式求最值，通过挖掘已知条件，对条件等式和欲求的式子进行重新整理，构造出可用基本不等式求解式子，化解了问题的难点．

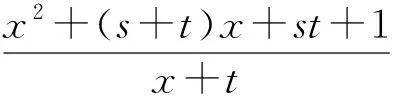
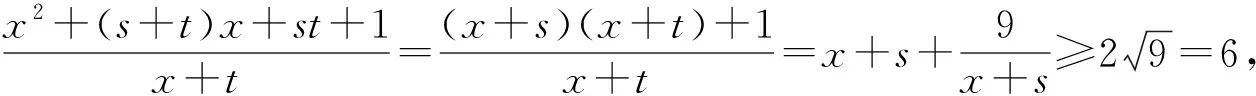
点评：本题若没有抓住x+s>0(正项)进行正确的配凑，而是把x+t当着变元，从而使解题造成混乱得出错解或使后续解题无法进行下去,容易出现误判.

二、换元减元

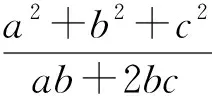
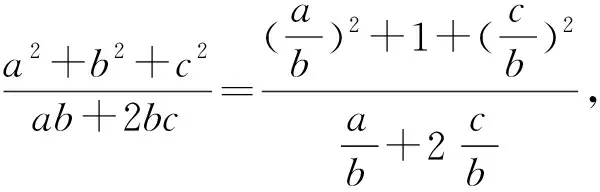
点评：本解法通过换元，将三个元素问题变成两个元素二次方程问题，为后面的配方解题提供了重要的信息和基础．

例4 已知关于的实系数一元二次不等式的解集为，则的最小值是．

点评：本题解法中，对变形后的式子的某个部分(特殊结构)进行换元处理，能够凸现出某些特定的解题形式，可以进一步引导、启发下面的求解．

三、变形重组

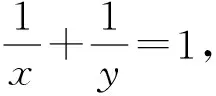
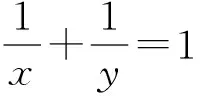
点评：由于条件式与结论式之间没有直接联系，所以需要对它们进行同时变形，使它们之间能够建立联系，通过变形后出现了一片光明前景．

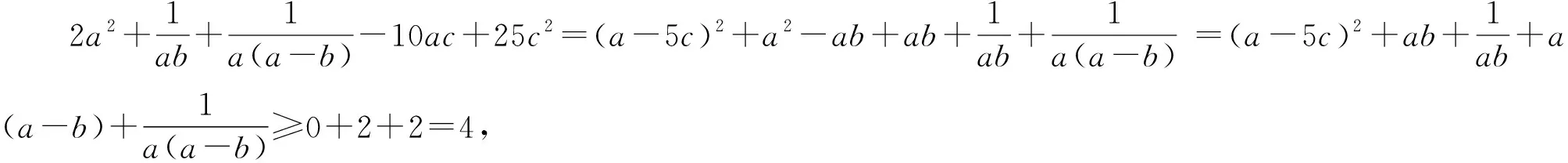
点评：题目中是有多个式子组成的，需要针对目标进行有效的组合，通过重新分组再同时运用基本不等式达到了解题目的，但需注意同时取等号的条件的满足．

四、多次放缩

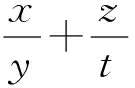
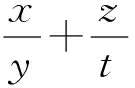
点评：本题有四个变量x、y、z、t，且变量间的关系比较松散，抓住求最小值这一个目标通过大小关系和范围进行适当的放缩，逐步减少了变量的个数，为运用基本不等式解题扫清了障碍．

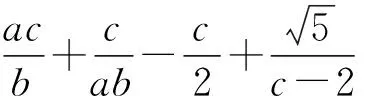
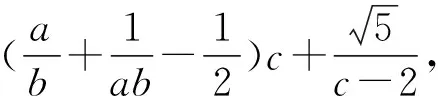
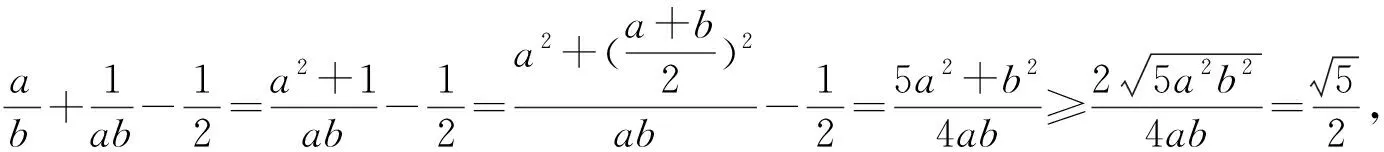
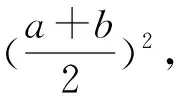
五、函数思想

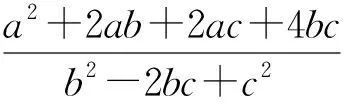
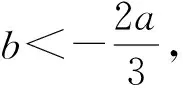
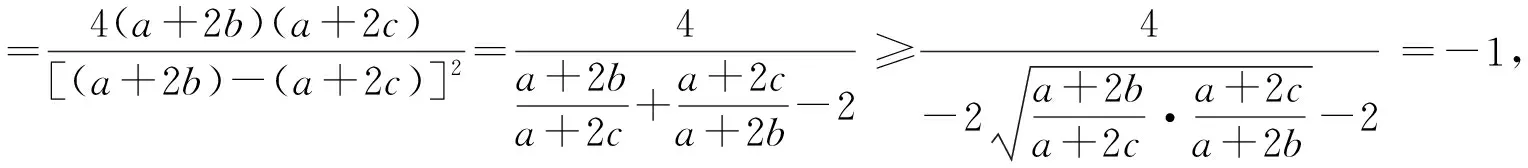
点评：题目中的函数条件非常重要，如何运用是成功解题的核心点，本题中给出的条件就是要判断a+2b与a+2c的正负号，必须把握好这一点．

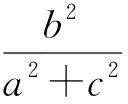
点评：本题中对不等式恒成立的条件理解是比较重要的，后续的替换变形是为寻找运用基本不等式解题的结构形式，一些常见的结构模型必须记清楚．