江苏省仪征市新集初级中学 (211403) 李爱民

1 原题呈现

图1

(1)当n=1时，①求线段AB所在直线的函数表达式；②你完全同意小明的说法吗？若完全同意，请说明理由；若不完全同意，也请说明理由，并求出正确的k的最小值和最大值；

(2)若小明的说法完全正确，求n的取值范围.

2 试题评析

本题叙述简约，函数图像简洁，结构合理，内涵丰富，重点考查学生逻辑推理、数学建模、数学运算等核心素养，是一道具备选拔功能的压轴题.函数是初中代数的核心知识，是中考考查的重点内容.本题最大的妙处是贯穿初中三个函数，题干是反比例函数，通过动点探究反比例函数k变化的性质；第(1)问中的第①问考查待定系数法求一次函数表达式，这是基础；第②问是命题判断和推理说明，考查数学建模、逻辑推理能力，这是素养.两个大问题设计层次分明，第(1)问中包含的两个问题，对解决第(2)问具备启发作用，考查学生特殊到一般、分类讨论等数学思想.该试题对教师的教学也具备一定的指导作用.

3 第②问典型解法呈现

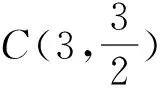
评注：列举法也能充分说明小明的说法不完全正确，因为说明一个命题错误，可以举一个反例，但对k最值问题的说理不充分，所以该解法不能得满分.此种解法说明这类学生还是具备一定的数学素养的，在列举点P经过的特殊点时，没有杂乱无章的取，而是不断取线段的中点，体现了逐步逼近的思想；在出现两个k值相等时，联想到二次函数的对称性，所以取了BD的中点E，认为点E就是二次函数顶点，经过点E处k值最大，这是几何直观.

图2

评注：解法二和三都是构造二次函数，考查了学生的建模思想.解法二是代入点坐标表示k值，解法三是通过双曲矩形(过双曲线上一点作x轴、y轴的垂线与坐标轴围成的矩形)的面积表示k值，两种方法都是求反比例函数k值的通法.学生能想到构造函数，正是本着对反比例函数性质的充分理解，也提醒我们教者教学时要注重基本知识、基本思想的渗透，不能求难求偏.

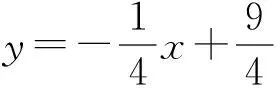
评注：函数和方程是两个不同的概念，但它们之间有着密切的联系，许多函数问题可以用方程的方法来解决，许多方程的问题也可以借助函数来解决，函数思想和方程思想是初中数学重要的数学思想.解法四就是将函数问题转化成方程问题来解决.

4 第(2)问典型的失误及分析

失误一：无法用待定系数法正确求解出含参的一次函数解析式.究其原因主要两个，一是计算失误；二是抽象能力不足，不能准确分辨参数和待定系数之间的差别，出现乱花迷眼、不知所措的情形.

情形1：无从下手，直接放弃.

从学生的失误中，我们不难发现学生存在的问题和学生的层次差别，试题的选拔性可见一斑.

5 教学思考

中考试题可谓千变万化，但是万变不离其宗，这个“宗”就是数学的核心知识和基本数学思想.因此，数学概念教学不能再搞“一个定义，三项注意”，解题教学不能再专注“题型+技巧”，必须要返璞归真，回归基础.中学数学的基础是那些为学生终身发展奠定的初等数学核心部分(章建跃).如何落实基础呢？笔者认为可以在如下几个方面努力：

5.1 立足核心知识，关注联系，培养系统思维

数学是一个系统，学习数学知识需要系统思维.所谓系统思维简单来说就是对事情全面思考，不是就是论事.用系统思维来学习数学也就是要有全局观和整体观，它可以将复杂问题简单化，提升抽象能力.函数是初中数学核心知识，也是中考命题的重点内容，更是压轴题的压点.初中阶段主要学习了一次函数，反比例函数，二次函数.初学一次函数如果能概括研究函数的结构系统(定义—图像性质—应用—与方程、不等式的关系)，那么在后续学习反比例函数和二次函数时，就能达到轻车熟路，轻松驾驭的效果.同样，学习函数性质时，我们通常从形状、位置、增减性、最值、对称性、平移、图像与自变量的系数关系等视角研究，这些构成了研究函数性质的结构系统.这些结构系统也可以迁移到其它知识的学习中，形成更大的系统.

系统思维方式通常具有整体性、结构性、动态性、综合性.本题第(1)问与第(2)问是特殊到一般的关系，如果学生能从整体角度把握试题，体会两个问题之间的逻辑关系，解决第(2)问的方法就会自然浮出水面，具体做法只需要在完成第(1)问后，概括出解决问题的结构系统，再迁移到第(2)问即可.第(2)问的难点是如何分类讨论，如果学生能调动研究函数性质的结构系统，抓住动点问题要把握整个运动的过程，分类也不是很困难.因为点A的位置确定，点B的位置不确定，所以点P从点A到点B运动的过程中有三种情形：上升、下降、水平，对应n>2，n<2，n=2.其中n<2的情形与第(1)问相同，那只需要做同样的探究即可.当n>2和n=2时，可以画出线段AB，再结合反比例函数图像关于y=x对称的性质和k与图像位置的关系，不难发现这两种情形小明的说法恒成立，问题解决.

5.2 强化知识理解，关注过程，提炼基本思想

章建跃博士认为数学思想方法如根，它是发现和提出问题的源泉，是分析和解决问题的根本；数学思想方法如手，它是解决问题的直接工具；数学思想方法如船，在没有解决问题的直接方法时，它可以帮助你“渡过难关”[1].数学思想从何而来，它就蕴含在平时的教学过程中，只要我们用心挖掘，引导学生深度理解知识，关注知识形成的过程，重视总结概括，数学思想自然会在潜移默化中落地生根.

本题蕴含函数和方程、数形结合、分类讨论、特殊到一般等诸多数学思想.例如在第②问中，正是学生具备函数思想，才能想到构造二次函数解决问题(解法二)；因为学生能深刻认识到反比例函数的几何意义，才能想到将求k值问题转化为面积问题(解法三)；因为理解函数与方程之间的关系，才能想到将函数问题转化为方程问题，这其中还包含了学生对反比例函数对称性的深刻认识，以及用平移运动的眼光、数形结合的方法，观察反比例函数图像变化，才分析得到△=0时，k值最大的结论(解法四).反之，没有这些数学思想的支撑，问题都得不到完整的解决，甚至直接丢盔弃甲，缴械投降.

5.3 聚焦知识再生，关注通性通法，提升核心素养

所谓核心素养指学生应具备适应终身发展和社会发展所需要的必备品格和关键能力.根据数学教育的终极培养目标可将数学学科核心素养具体表述为：数学抽象、直观想象、逻辑推理、数学运算、数学建模和数据分析.当前中考试题命制更注重考查学生数学核心素养和学生思维能力，这就要求老师要把教学目标定位为核心素养的养成.指向核心素养的教学，要求教师抓住每个概念、定理的学习，每个问题的解决，启发学生积极思考探索，自主构建，归纳总结，积累经验，逐步提升素养.因为每个结论的探索都是知识再生的过程，它能很好地培养学生创新能力，当学生能用旧知解决新的问题，说明学生的核心素养已经生成.当然，教师要引导学生采用通性通法解决问题，通性通法更接近问题的本质，只有抓住本质，才能实现创生.

本题第(1)问中第②问考查了逻辑推理素养；学生通过构造函数解决问题，正是考查了数学建模素养；整个推理、建模的过程需要大量的运算，所以还考查了数学运算素养.学生用构造二次函数解决问题②，是基于“构造函数”是用代数法求最值的通性通法.构造函数采用了两种方法：点坐标法和面积法，这两种方法是求反比例函数k值的通性通法.