吴亚平，冯丽珠

（江汉大学 人工智能学院，湖北 武汉 430056）

0 引言

拟阵的概念是由Whitney［1］在1935年和Rado［2］在1942年分别提出的，1959年，Tutte［3］发展了这一概念。二十世纪拟阵论得到了空前的发展，拟阵论为组合优化和算法设计提供了强有力的工具。拟阵主要研究内容包含基图、超平面、和图、连通性等。2010年，李萍［4］提出了拟阵圈图的概念，研究了拟阵圈图的连通度、拟阵圈图中的圈和路的性质。文献［5-9］研究了拟阵圈图的其他性质。2020年，刘彬等［10］研究了在某些条件下均匀拟阵二阶圈图的哈密顿性。本文将研究均匀拟阵的三阶圈图的哈密顿性。由于均匀拟阵的三阶圈图是其相应二阶圈图的子图，所以若均匀拟阵三阶圈图是哈密顿的，则其二阶圈图一定是哈密顿的。

关于拟阵的相关术语可参考文献［11］。一个拟阵M是一个有序对(E,ℐ)，其中E是一个有限集合，ℐ⊆2E是E中子集的集合，它们满足以下的公理：

(I1)∅∈ℐ；

(I2)若I∈ℐ 且I′⊆I，则I′ ∈ℐ；

(I3)若I1,I2∈ℐ 且|I1|＜|I2|，则存在e∈I2-I1使得I1⋃e∈ℐ。

其中，集合ℐ 中的元素称为拟阵M的独立集。设M(E,ℐ)是一个拟阵，若子集X∉ℐ，则X称为M的一个相关集。极小的相关集叫做极小圈，令C(M)表示由拟阵M的全体极小圈组成的集合。

设n≥m≥0 为两个整数，E是个n-元集。令ℐ ={X⊆E:|X|≤m}，则M(E,ℐ)是个均匀拟阵，记作Um,n。均匀拟阵Um,n的k阶圈图为G，其中顶点集V(G)=C，边集E(G)={CC′|C,C′∈C,|C⋂C′|≥k}。这里C和C′既代表G的顶点，也代表拟阵M的圈。

关于图论的术语参考文献［12］。设G是一个图，包含图G的每个顶点的路称为图G的一条哈密顿路；包含图G的每个顶点的圈称为图G的一个哈密顿圈；如果图G存在一个哈密顿圈，则称之为哈密顿的。如果图G中的每对顶点u,v都存在一条u到v哈密顿路，则称图G是哈密顿连通的。如果对于图G的任意一条边，G都有一个包含这条边的哈密顿圈，则称G是正哈密顿的；如果对于图G的任意一条边，G都有一个不包含这条边的哈密顿圈，则称G是负哈密顿的。如果G既是正哈密顿的，又是负哈密顿的，则称G是一致哈密顿的。

设G是一个图，如果G中的任意两个顶点都相邻，则称G是完全图。

1 预备知识

引理1［12］设G是一个n-阶图，其中n≥3。如果G的每个顶点v都有那么G是哈密顿连通的。

引理2U3,n的三阶圈图共有个顶点，并且是正则图，其中n≥5，且n为正整数。

证 明令E={x1,x2,…,xn}，C(U3,n)={X⊆E:|X|= 4}，从n个 元素中 选取4 个 元素可 以作为U3,n三阶圈图的一个顶点，所以U3,n的三阶圈图共有(n)4 个顶点。任取U3,n的三阶圈图的一个 顶 点{xi,xj,xk,xs}，其 中i≠j≠k≠s且i,j,k,s∈{1,2,…,n}。从{xi,xj,xk,xs}中 的 任取3 个元素，剩下的一个元素需从除了xi,xj,xk,xs之外的n- 4 个元素中选择，故与{xi,xj,xk,xs}相邻的顶点有个。又由{xi,xj,xk,xs}的任意性知，U3,n的三阶圈图是正则图。

引理3U4,n的三阶圈图共有个顶点，并且是正则图，其中n≥6，且n为正整数。

证明令E={x1,x2,…,xn}，C(U4,n)={X⊆E:|X|= 5}，从n个元素中选取5 个元素可以作为U4,n三阶圈图的一个顶点，所以U4,n的三阶圈图共有个顶点。

采用与引理2 类似的证明，任取U4,n的三阶圈图的一个顶点A={xi,xj,xk,xl,xs}，其中i≠j≠k≠l≠s且i,j,k,l,s∈{1,2,…,n}。下面我们求与A相邻的顶点的个数。如果A的邻点与它恰好有3 个元素相同，则满足这个条件A的邻点个数为如果A的邻点与它恰好有4 个元素相同，则满足这个条件A的邻点个数为

所以与A相邻的顶点共有个。又由顶点A的任意性可知，U4,n的三阶圈图是正则。

引理4Um,n的三阶圈图共有个顶点，并且是正则图，其中m,n均为正整数，且m≥3,n≥m+ 2。

证明令C(Um,n)={X⊆E:|X|=m+ 1}。由定义知Um,n的三阶圈图共有个顶点。下面证明Um,n的三阶圈图是正则图。

同引理3 证明，任取Um,n的三阶圈图的一个顶点B={xi1,xi2,…,xim+1}，其中ij≠ik，j≠k，ij∈{1,2,…,n},j= 1,2,…,m+ 1。下面求与B相邻的顶点的个数。如果B的邻点与它恰好有k(3≤k≤m)个元素相同，则满足这个条件B的邻点个数为所以B的 邻点个数由于B的任意性，可知Um,n的三阶圈图是正则图。

引理5［10］若G是完全图，则G是哈密顿连通的，并且是一致哈密顿的。

2 主要结论

在证明主要结论中，需要用到Pascal 公式和下面这个组合恒等式：

定理1当m+ 2≤n≤2m- 1，m≥3，Um,n的三阶圈图是哈密顿连通的，并且是一致哈密顿的。

证明由引理4 可知，Um,n三阶圈图顶点数是它是正则图。

根据式（1），有

当m+ 2≤n≤2m- 1，可知故

可知

即当m+ 2≤n≤2m- 1，m≥3，Um,n的三阶圈图是完全图。由引理5 可知，Um,n的三阶圈图是哈密顿连通的，并且是一致哈密顿的。

定理2Um,2m的三阶圈图是哈密顿连通的，m≥3。

证明由引理4 可知，Um,2m三阶圈图顶点数是它是正则的。

首先证明一个断言。

断言

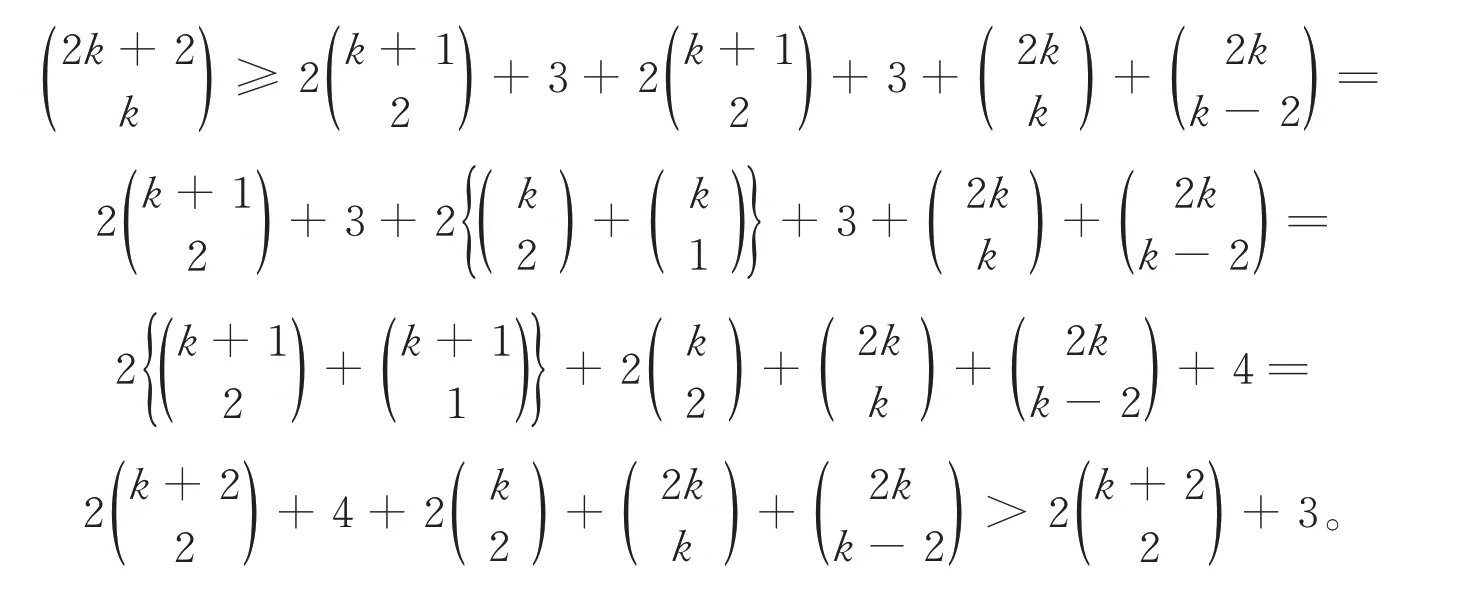
因此断言成立。

根据式（1）可知，

根据断言，则有

即

根据引理1，可知Um,2m的三阶圈图是哈密顿连通的。