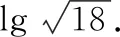高一学生对对数函数理解的研究
——以广东省中山市某高中为例
2020-10-21广东省中山市华侨中学528400
韩 聪 (广东省中山市华侨中学 528400)
1 问题提出
“对数”是符号化的数学,因抽象难懂使其成为高中生难以理解的概念之一[1]. 国外学者Kastberg认为在教学时,最难教的概念就是对数函数[2]. 对数函数是高一的内容,既然对数这么难学,对数函数如此难教,对数函数内容在高考中又高频出现,那么高一学生关于对数函数的学习表现如何,在学习过程中存在哪些学习困难都是很值得研究的问题. 弄清这些问题可以更有针对性地帮助学生克服学习困难,对教师教学也有一定的指导作用.
2 研究的设计
2.1 研究对象
在广东省中山市某中学高一年级随机选取6个班的学生作为研究对象. 样本中,男生125人,女生204人;文科166人,理科163人;重点班110人,平行班219人. 受便利样本的影响,样本中男女生人数略有差异,文理科人数基本持平.
2.2 研究工具
包括测试卷和问卷,其中测试卷用来了解学生对数函数的学习表现和学习困难,问卷主要用来测量学生关于对数函数的情感态度.
结合文献与《考试大纲》的知识要求,自编测试卷[3-5]. 测试卷从对数的概念、对数的运算性质、对数函数的概念、对数函数的图象和性质四个维度考查学生对对数函数相关内容的理解和掌握情况. 在正式测验前先对测试卷进行预测,并对测试题目进行修改和完善,形成了最终测试卷.
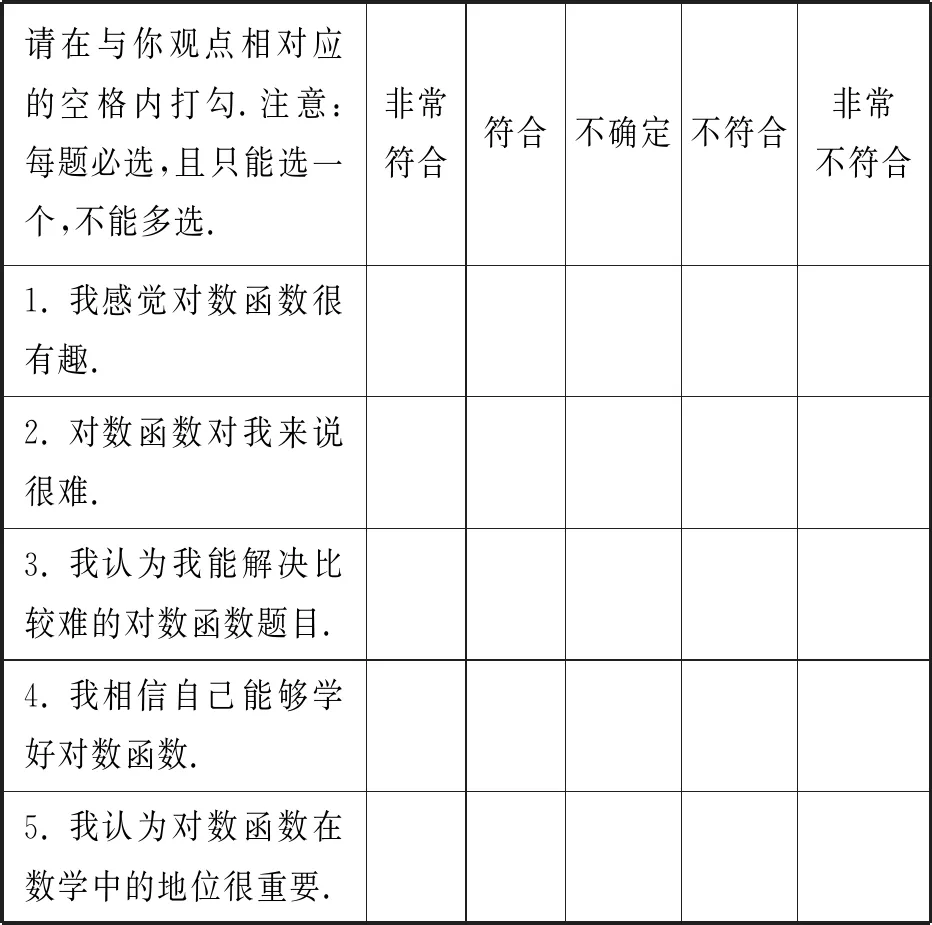
问卷主要测量高一学生学习对数函数时所表现的学习兴趣、自我效能感和学习动机. 施测项目共5题,每题采用李克特量表5级计分方式,从5(表示“非常符合”)到1(表示“非常不符合”). 得分越高说明学生对对数函数的情感态度越积极. 题目主要参考了赵闻敏、王中雷等人设计的问卷[6-7].
本研究共发放调查卷329份,收回有效调查卷共313份,有效率为95.14%.
3 数据整理与分析
3.1 测试卷总体情况
表1呈现了学生在对数函数内容四个维度上的表现. 从表中数据可见,高一学生在对数概念和对数函数的概念这两个维度得分率较高,对数的性质其次,对数函数的图像和性质维度得分率最低. 笔者认为,对数概念和对数函数概念涉及到的知识点较少且二者相关性强,故二者得分率较高;而对数的性质和对数函数的图像和性质由于涉及知识点较多,考点较综合,故学生掌握较差.
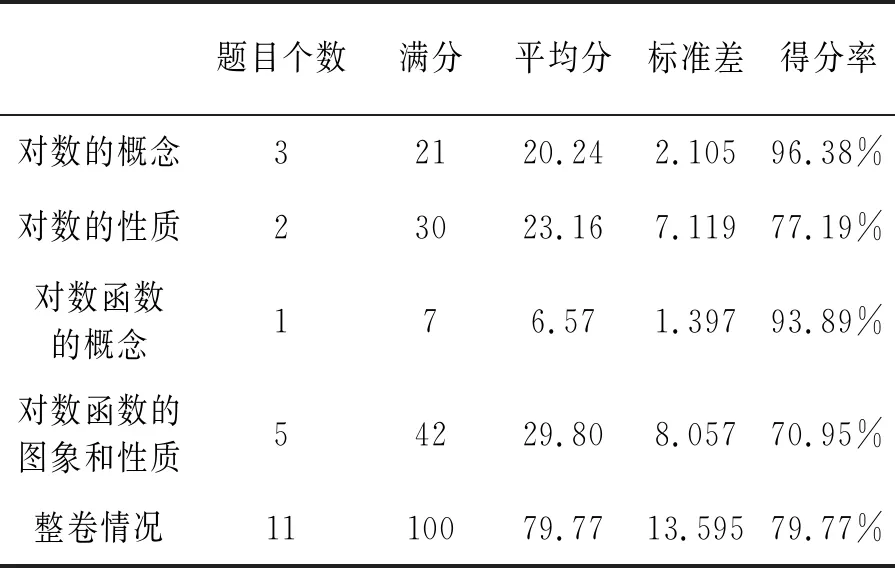
表1 高一学生在不同维度上的总体表现
3.2 学生对对数函数的情感态度分析
学生的学习动机较强,自我效能感次之,兴趣很低. 学生对对数函数的情感态度与对数函数测试成绩呈显著正相关,数据详见表2、表3.
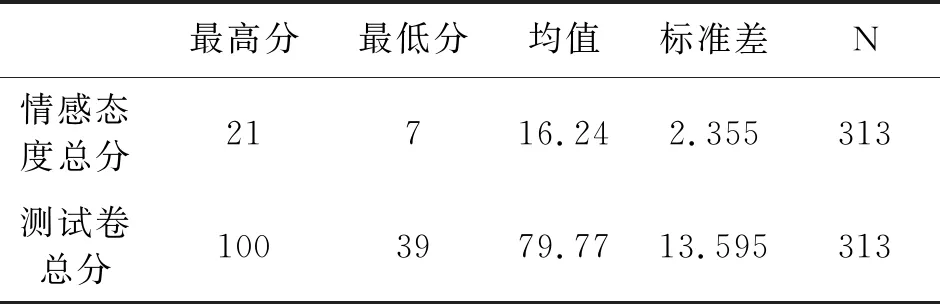
表2 情感态度、测试成绩基本情况

表3 情感态度与学习表现之间的相关分析
**表示在0.01水平(双侧)上显著相关
4 结果分析
4.1 对数函数四个维度的学习表现
(1) 在对数概念维度,学生能解题,但不理解对数的概念
超过93%的高一学生可以完成指对互化、知道真数大于0、能记住两个常用结论“logaa=1,loga1=0(a>0,a≠1)”. 但不能从指数出发理解对数各要素的含义,也不理解对数符号的意义. 此外,也有学生混淆三种符号log,lg和ln.
(2) 在对数的运算性质维度,能完成对数的简单运算,机械记忆公式明显
超过70%的学生能运用对数的运算性质进行基本运算,模仿解题. 但当题目结构与运算法则不同时,解题正确率则下降至50%,并衍生出各种各样的错误“性质”. 也就是说,将近一半的学生采取机械记忆的方式背诵对数的运算性质,不能从根本上理解对数运算的本质.
(3) 在对数函数概念维度,知道对数函数定义域,但会忽略对定义域的考察
在对数函数概念维度,有近95%的学生知道对数函数的定义域,但当题目较综合没有直接考察定义域时,则有26.20%的学生会忽略对定义域的考察.
(4) 在对数函数的图象和性质维度,知道对数函数的单调性,但分类讨论意识不足
主要体现在当底数是一个未知量时,只有87%左右的学生意识到要进行分类讨论才能判断单调性. 在函数图象上,有些学生分不清指数函数和对数函数的图象,画错图象,不理解图象过定点的含义. 在运用图象和性质比较大小问题上,有7.35%的学生不会比较大小或不会选择合适的中间量比较大小.
4.2 学习对数函数时出现的学习困难
(1)符号理解困难
数学符号可以分为元素符号、运算符号、关系符号和辅助符号[8]. 对数符号属于运算符号. 在对数的运算性质维度和对数函数的图象和性质维度的调查中都显示学生在对数符号的理解上存在困难,主要体现在不能将对数符号logab视为一个整体,看作是一种运算,而是将其视为loga和b的乘积关系,在进行对数运算和对数不等式的求解时出现将loga看作因式提取或约去的现象.
(2)运算性质理解困难
学生在对数运算性质的运用上呈现出机械模仿的特征,死记硬背公式明显. 学生对对数运算性质的理解仅达到工具性理解阶段,尚未达到关系性理解. 可以运用公式解决简单的化简求值问题,但还不能解决一些需要较高认知水平的题目.
(3)数学思想应用困难
分类讨论思想是一种重要的数学思想,在对数函数单调性的判断上离不开对底数的分类讨论. 当底数是常数时,学生不难判断函数的单调性. 但当底数是未知数a时,则有学生不知道要对底数进行分类讨论才能判断函数单调性.
(4)复合函数理解困难
从函数y=loga(3x-4)图象过定点问题发现,学生不知道对数函数与对数型函数的区别,不能将函数y=loga(3x-4)视为对数函数和一次函数复合而成的复合函数,误以为对数函数y=logax图象与对数型函数y=loga(3x-4)图象经过相同的定点.
4.3 有关对数函数的情感态度
对于对数函数的学习,高一学生表现出学习兴趣不浓,不知道学习对数函数有什么用. 自我效能感也比较低. 尽管学生对对数函数的学习动机较强,但往往是从考试为出发点,而不是源于对对数函数应用价值的认识. 学生对对数函数的情感态度与对数函数测试成绩呈显著正相关.
5 教学建议
(1) 重视概念的形成过程
“对数”是符号化的数学,抽象的符号定义给学生的理解带来了困难[9].学生如果不能理清对数符号、底数、真数之间的关系,必将直接影响对数运算性质的理解和运用,导致数学推理的错误. 因此,教师在对数概念教学时应着重强调对数符号中底数、真数的含义,利用好指对互化,规范学生对数符号的书写,帮助学生从本质上理解对数的概念.
(2) 加强对数运算本质的理解,克服负迁移带来的消极影响
迁移是一种心理现象,是一种学习对另一种学习所产生的影响. 迁移有正迁移和负迁移之分. 认知心理学认为,如果认知结构的功能出现偏差或某个认知环节有缺陷,便会出现学习中的负迁移[10]. 对数运算与四则运算的结构不同,学生对对数符号的错误理解导致运算性质的学习出现偏差,得出一些错误结论.
(3) 充分利用教材中的阅读材料
通过访谈得知,绝大多数教师并没有介绍对数的发展历史及其在简化运算中的作用,学生也没有阅读教材中关于对数历史的阅读材料. 也就是说学生对对数简化运算的作用一无所知,完全感受不到引入对数的必要性. 这种情况下学习对数,学生无疑会觉得非常突兀. 笔者认为教师在教学中应向学生介绍对数的发展史,或引导学生学习教材中的阅读材料,充分体会引入对数的必要性.
附录一 测试卷
1. (7分)把3a=b改写为对数式;把改写为指数式.
2. (7分)使对数loga(4-a)有意义的实数a的取值范围是
( )
A.a<4 B.0 C.a>0,且a≠1 D.0 3. (7分)已知数log5(log2x)=0,求x的值. 5.计算((1)、(3)每题7分,(2) 9分): (1)log354-log38+log34 (2) lg 21g 50+1g 5lg 20-lg 100lg 51g 2 (3) log34×log29 6. (7分)函数y=log3(3x-2)的定义域为. 8. (7分)已知lnx 9. (12分)求使不等式loga(x+1)>loga(1-x)成立的x的集合,其中a>0且a≠1. 11. (5分)函数y=loga(3x-4)图象过定点.(其中a>0且a≠1) 附录二 测试卷