刘 畅,曾以成

(湘潭大学物理与光电工程学院,湖南湘潭 411105)

1 引言

自1990年,Ott等[1]基于参数微扰的方法第一次成功实现了混沌系统的控制以来,关于混沌控制的问题就一直吸引着人们不断地进行探索.混沌控制分为两大研究方向,其一是增强混沌[2–3],即增强混沌系统动力学行为的复杂性,利用混沌的长期不可预测性和内在伪随机性来进行保密通信[4–5]、图像加密[6]、产生伪随机数[7]等.近年来,研究最多的增强混沌的方法,是实现吸引子的多涡卷化,或多翅膀化,具体方法包括扩展指标2的鞍焦点[8]、状态反馈控制[9]以及引入忆阻器[10]等.其二是抑制混沌[11–12],在需要避免非线性系统进入混沌状态时,或不希望非线性系统出现强混沌状态时,则通过某种控制策略控制非线性系统进入非混沌的目标状态,或通过一些方法削弱非线性系统的混沌强度.例如在电子系统的分析和设计中要避免出现混沌以求系统的稳定性和可靠性[13].然而,通过退化吸引子,即减少吸引子涡卷数,从而抑制混沌的研究却很少见.

最近,Natiq等[14]通过构造2个非线性控制器,将等离子体扰动系统的两翼蝴蝶吸引子分裂为一对共存的单翼吸引子,而后均退化为周期轨道,其控制实质是分离了等离子体扰动系统的平衡点.平衡点的存在性及其稳定性是混沌系统产生多涡卷吸引子的关键因素,尤其是指标2的鞍焦点,它是系统产生涡卷运动的前提.因此,在非线性多涡卷系统中,深入研究移动平衡点或减少平衡点的数量来逐渐减少多涡卷吸引子的涡卷数从而达到抑制混沌目的是非常有意义的,将进一步揭示非线性系统中平衡点和吸引子涡卷之间的关系.

2011年,Sharma等[15]提出了线性增量控制,该方法最初的目的是稳定非线性系统的不动点,后来被应用在控制驱动–响应系统的动力学行为[16],以及减少多稳态系统中的稳态[17–18]等方面.仔细研究后发现线性增量控制实际上是通过控制平衡点的移动来达到控制目标的,与文献[14]中的控制对象一致.

受上述分析启发,将线性增量控制方法应用于非线性多涡卷混沌系统中,研究其对吸引子退化及抑制混沌的控制作用.并以经典的三维Lorenz 两翼系统[19]、三维四翼系统[20]以及新四维风车型四翼系统为例,验证线性增量控制在不同维数不同涡卷数混沌系统中减少吸引子涡卷数从而抑制混沌的有效性.

2 线性增量控制

实施线性增量控制的动力系统的一般表达形式为

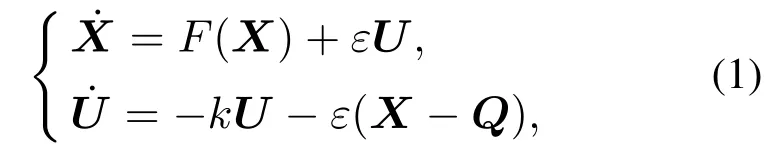
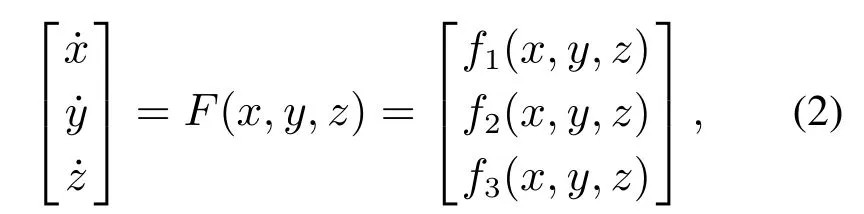
其中:x,y,z为非线性系统的状态变量,F(x,y,z)为状态函数.将线性增量控制应用到系统(2)中,以耦合在x状态变量方程为例,将得到如下4D非线性系统:

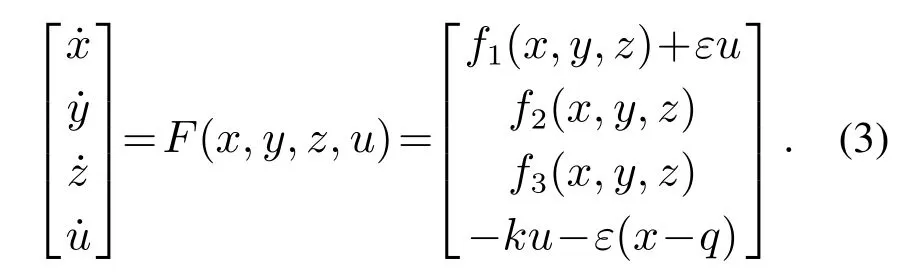
根据系统(3)的表达形式可知,如果状态函数已知,则能分析系统平衡点的存在性及其稳定性,进而研究线性增量控制对吸引子退化及抑制混沌的控制作用.因此在后续论述中笔者结合具体的多涡卷非线性系统进行分析讨论.

3 三维Lorenz两翼吸引子系统

经典Lorenz系统的状态方程为

如图1中的圆点所示.根据平衡点处的Jacobian矩阵,可得到相应的特征值方程,其特征值解中实部为正数的个数即为指标[22].通过计算得Lorenz系统3个平衡点处的特征值分别为

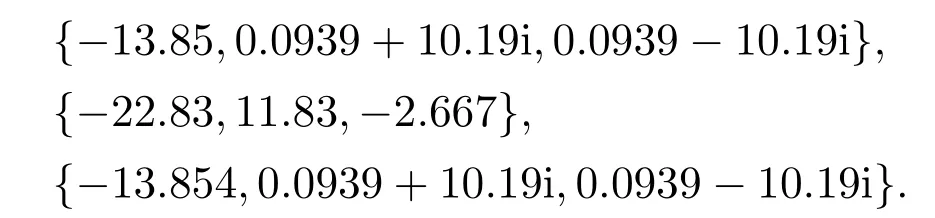
因此S1和S3是指标2的鞍焦点,S2是指标1的鞍点.

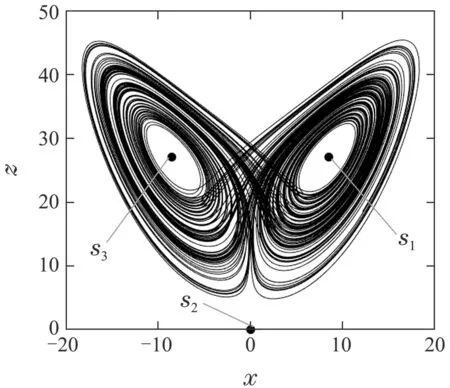
图1 Lorenz系统两翅膀吸引子Fig.1 Two-wing attractor of Lorenz system

引入线性增量控制后,系统(4)将变为如下四维非线性系统:

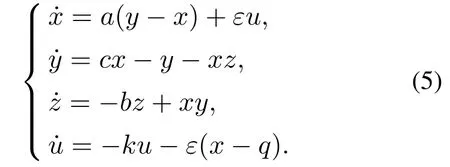
取k=1,q为平衡点S1的x坐标,即

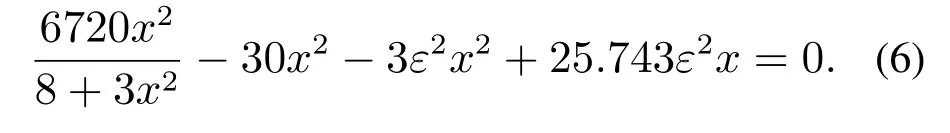
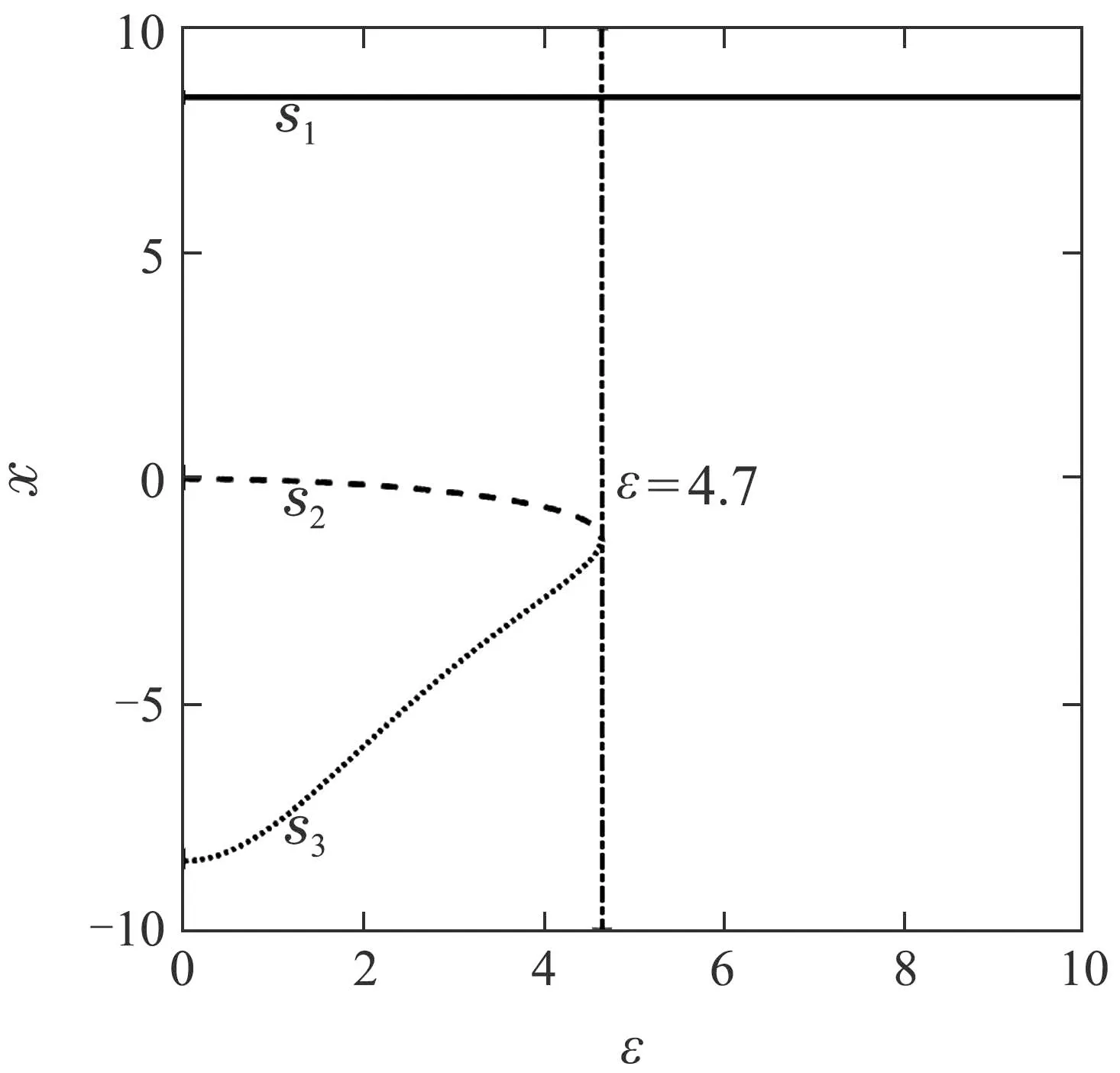
图2 系统(5)3个平衡点的x坐标随ε增大的移动曲线Fig.2 x(ε)curves of three equilibria of system(5)

根据图2,可以发现随着耦合参数ε逐渐增大,平衡点S1的坐标位置不变,而S2和S3两个平衡点互相靠近,最终于ε=4.7 时重合后消失.只剩下一个平衡点S1(8.4858, 8.4858, 27, 0.0012),且其特征值为{−12.5, 0.0384+10.5i,0.0384−10.5i, −2.243},依然是指标2的鞍焦点.在Lorenz两翅膀吸引子中,2个指标2的鞍焦点S1和S3是产生2个翅膀的关键,而指标1的鞍点S2是连接2个翅膀之间键带形成的基础.S2和S3两个平衡点的消失将使得两翅膀吸引子中围绕平衡点S3的翅膀消失,只剩下围绕平衡点S1的单翅膀,呈现出两翅膀到单翅膀的变化趋势.当ε继续增大,Lorenz系统受到线性系统的影响增强,混沌强度将被逐渐减弱,最终稳定在周期状态.随耦合参数ε变化的系统状态变量x的分岔图以及相应的Lyapunov指数谱证明了整个Lorenz系统混沌强度减弱的过程,如图3所示.根据分岔图和Lyapunov指数谱选取ε的值,得到特定形态吸引子在x–z平面的相轨图,如图4所示,初始条件为(2.9,−1.3, 25, 0.1).

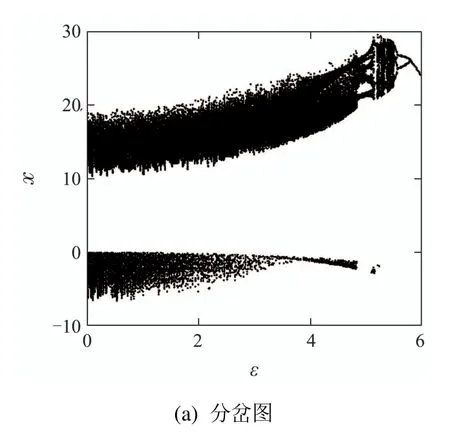
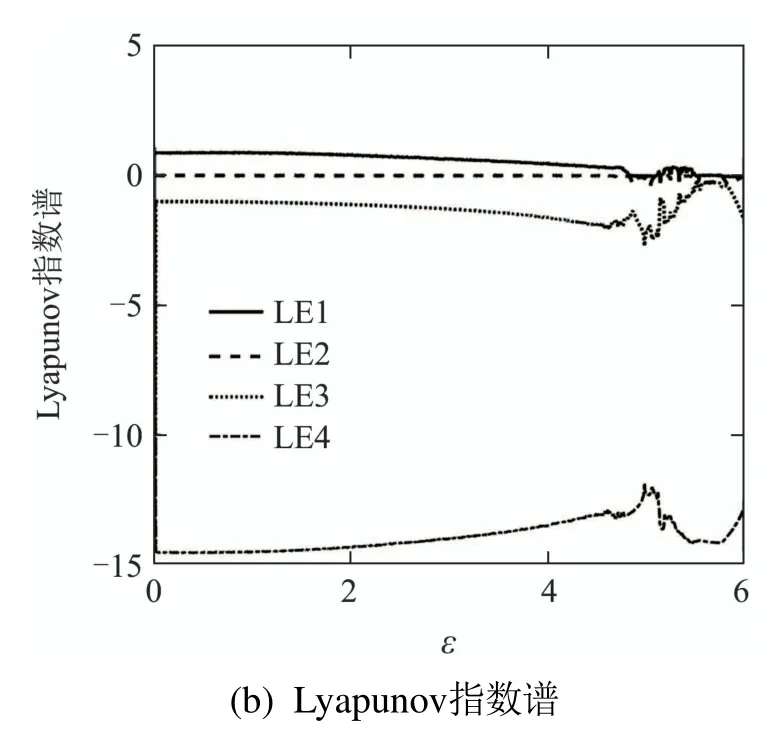
图3 系统(5)分岔图和Lyapunov指数谱Fig.3 Bifurcation diagram and Lyapunov exponent spectrum of system(5)

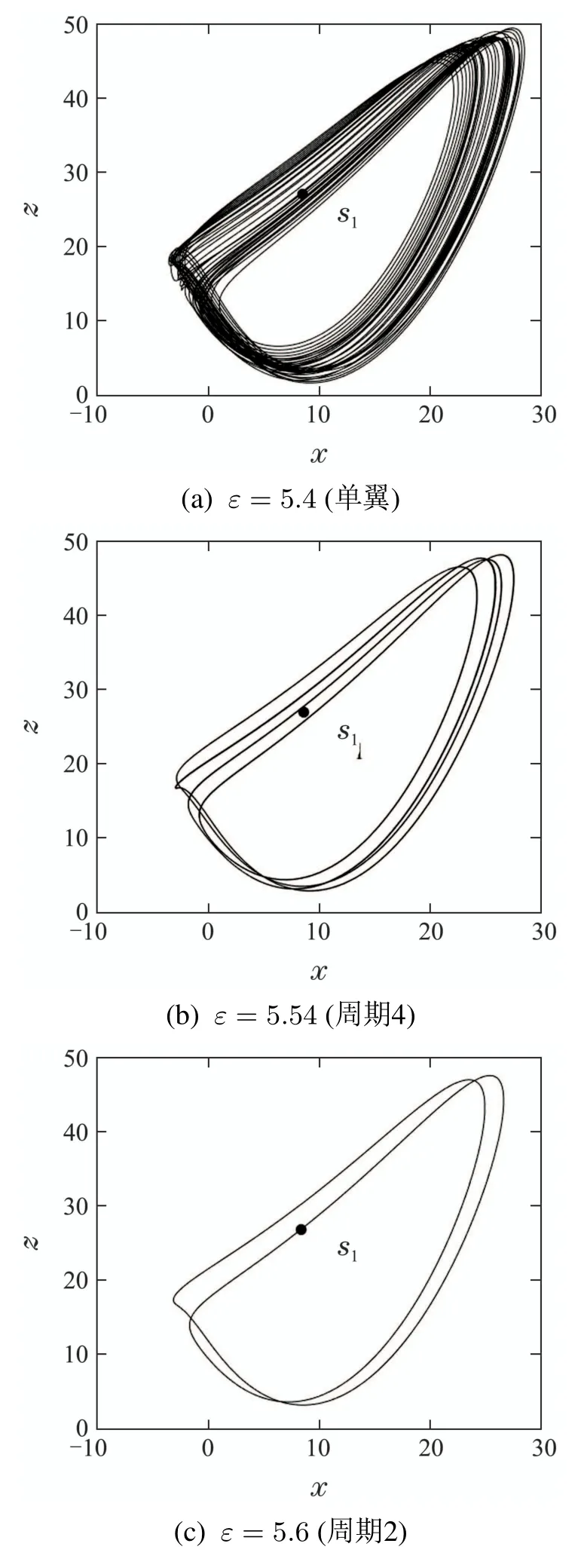
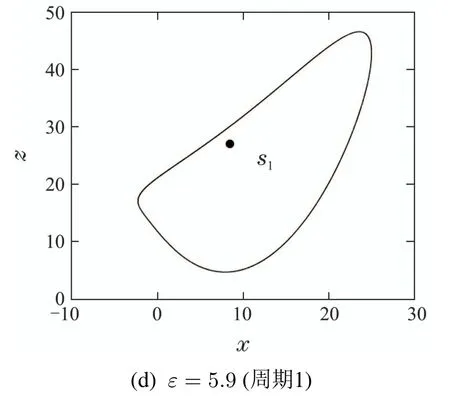
图4 系统(5)吸引子在x–z平面的相轨图Fig.4 Phase portraits of attractor of the system(5)in the x–z plane

另外,当取q=x3=−8.4858时,可以得到相同的控制结果.通过计算可得此时系统(5)的3个平衡点x坐标的计算方程式如式(7)所示.3个平衡点的x坐标随耦合参数ε增大而移动的曲线如图5(a)所示,可以发现此时坐标位置不变的平衡点是S3,消失的平衡点是S1和S2,最终的周期1极限环将围绕平衡点S3,如图5(b)所示.

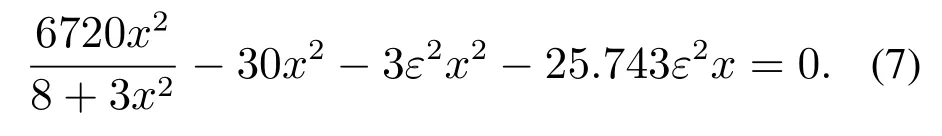
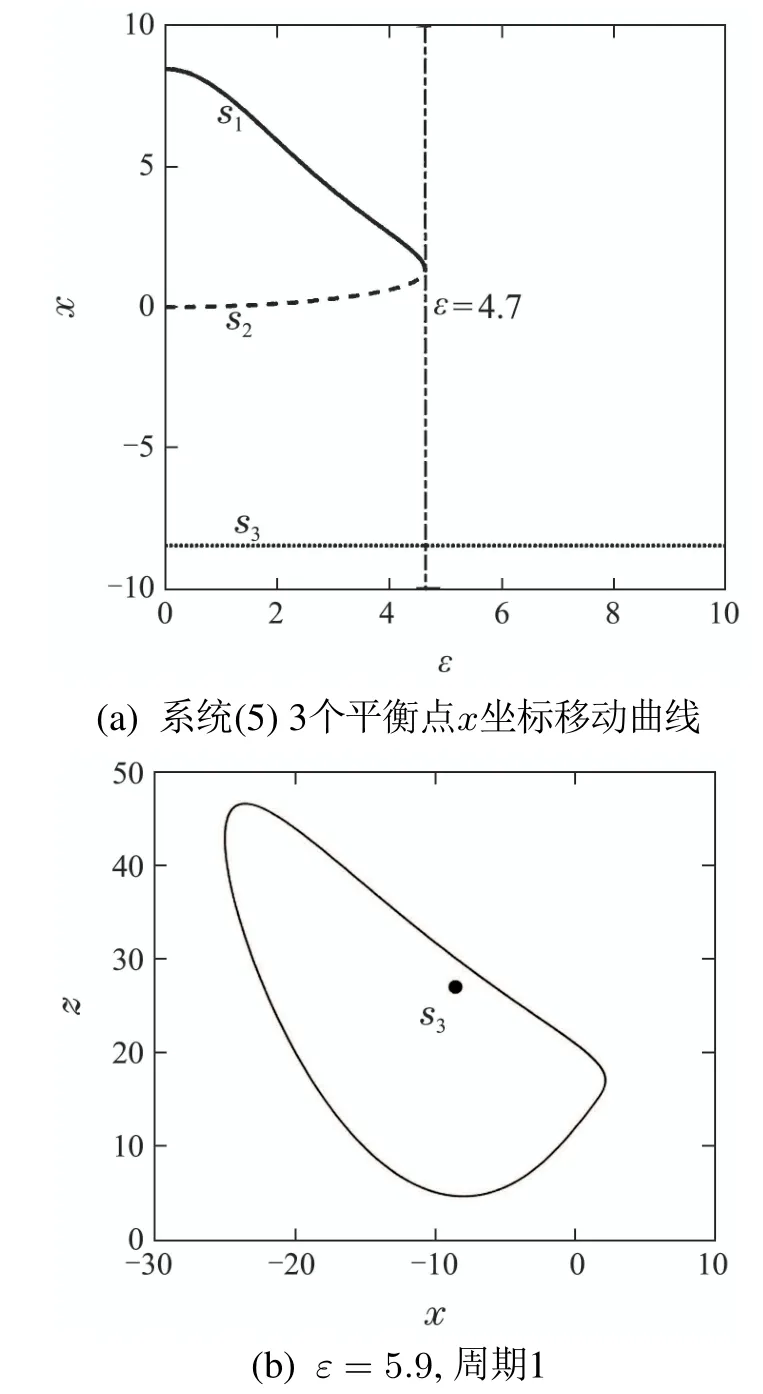
图5 q=x3=−8.4858,系统(5)Fig.5 System(5)at q=x3=−8.4858

4 三维四翼吸引子系统

在三维四翼吸引子系统中引入线性增量控制,可得到四维非线性系统如下所示:

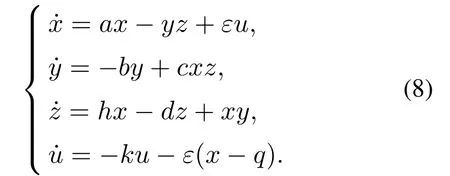
当ε=0时,即未控制情况下,三维四翼系统在参数a=3,b=8,c=4,h=1,d=2以及初始值条件(0.1,0.1,0.1)可产生一个四涡卷吸引子,且有5个平衡点:S1(2.4495,−3,−2.4495), S2(1.6630,2,2.4495), S3(0,0,0),S4(−1.6630,2,−2.4495)以及S5(−2.4495,−3,2.4495),如图6所示.经过计算知S1,S2,S4,S5是指标2的鞍焦点,S3是指标1的鞍点.

取k=1,q=x2=1.6630,且令=0,通过计算,得到系统(8)5个平衡点x坐标的计算方程如式(9),根据式(9)得到5个平衡点的x坐标随ε增大而移动的曲线如图7所示.

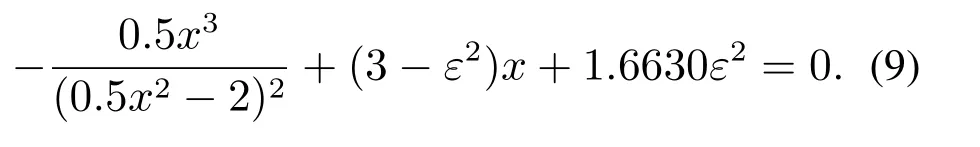
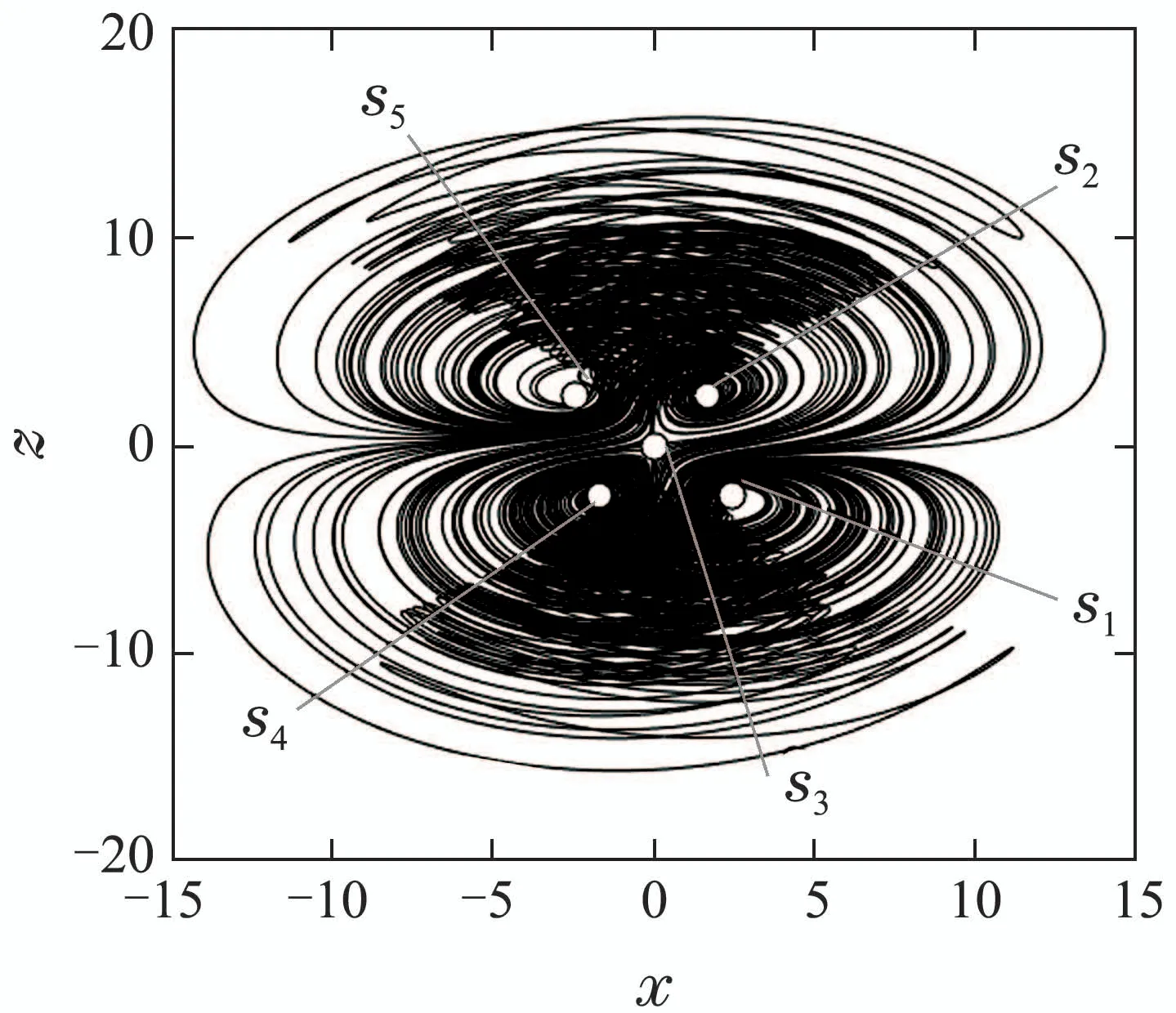
图6 ε=0,四涡卷吸引子Fig.6 Four-scroll attractor for ε=0

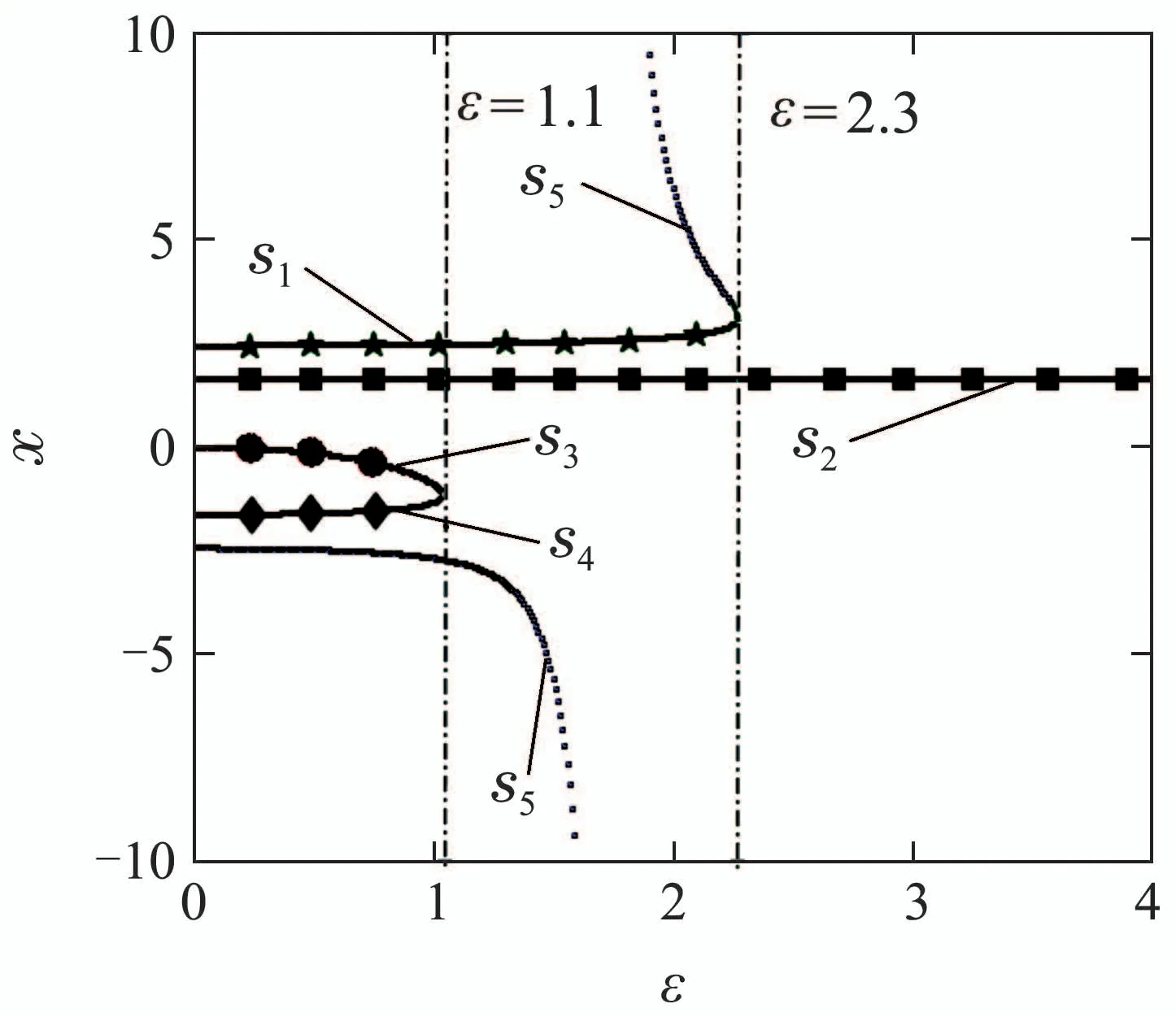
图7 系统(8)5个平衡点的x坐标随增大的移动曲线Fig.7 x(ε)curves of five equilibria of system(8)

根据图7,可以发现随着耦合强度ε的增大,S2的坐标位置保持不变,S3和S4两个平衡点的x坐标逐渐靠近,当ε=1.1 时,S3和S4两个平衡点重合后消失.而S1和S5两个平衡点会逐渐远离平衡点S2而后S1和S5互相靠近,当ε=2.3时也重合后消失,最终只剩下平衡点S2.此时其坐标为S2(1.6630,2,2.4495,0),相应的特征值为{−8.592,0.7485+4.927i,0.7485−4.927i,−0.9050},依然是指标2的鞍焦点.从0开始增大ε的过程中,系统吸引子呈现出从四涡卷变为三涡卷、二涡卷、单涡卷的趋势,最终稳定在围绕平衡点S2的周期1极限环,如图8所示,系统初始值为(0.1,0.1,0.1,0.1).随耦合参数ε变化的系统状态变量x的分岔图以及相应的Lyapunov指数谱也证明了这个系统混沌退化的过程,如图9所示.

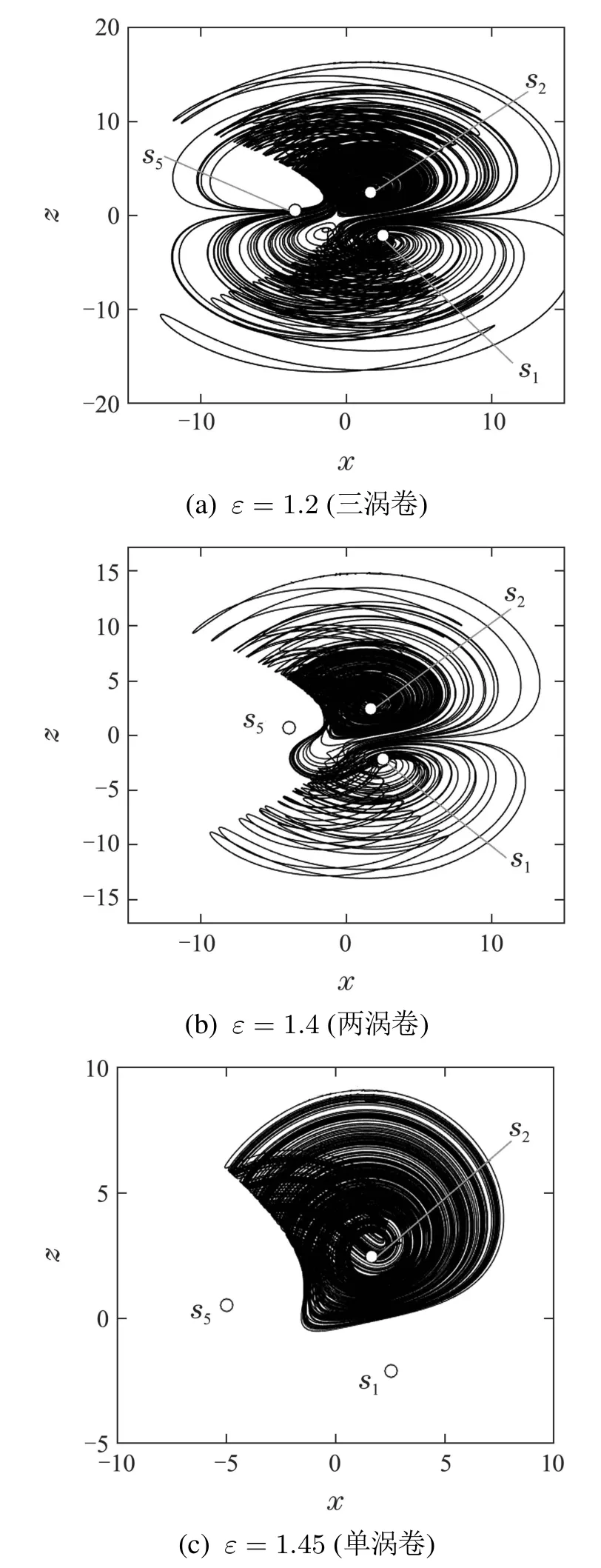
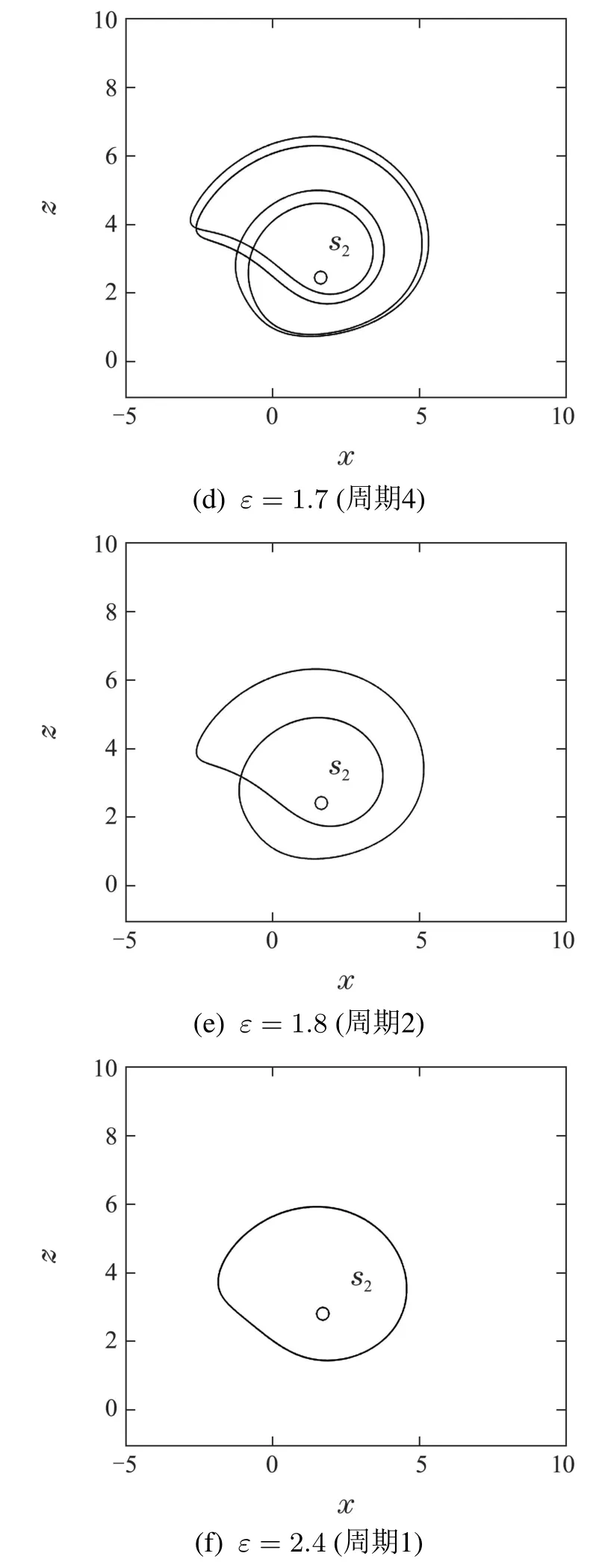
图8 系统(8)吸引子在x–z平面的相轨图Fig.8 Phase portraits of attractor of the system(8)in the x–z plane

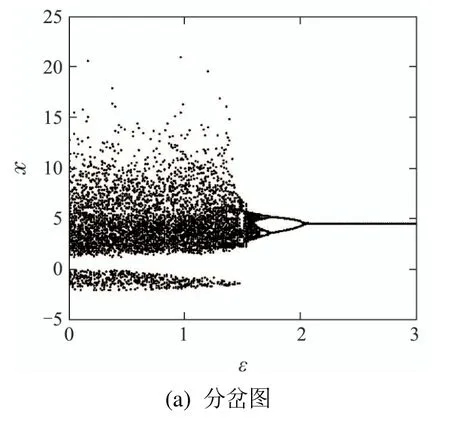
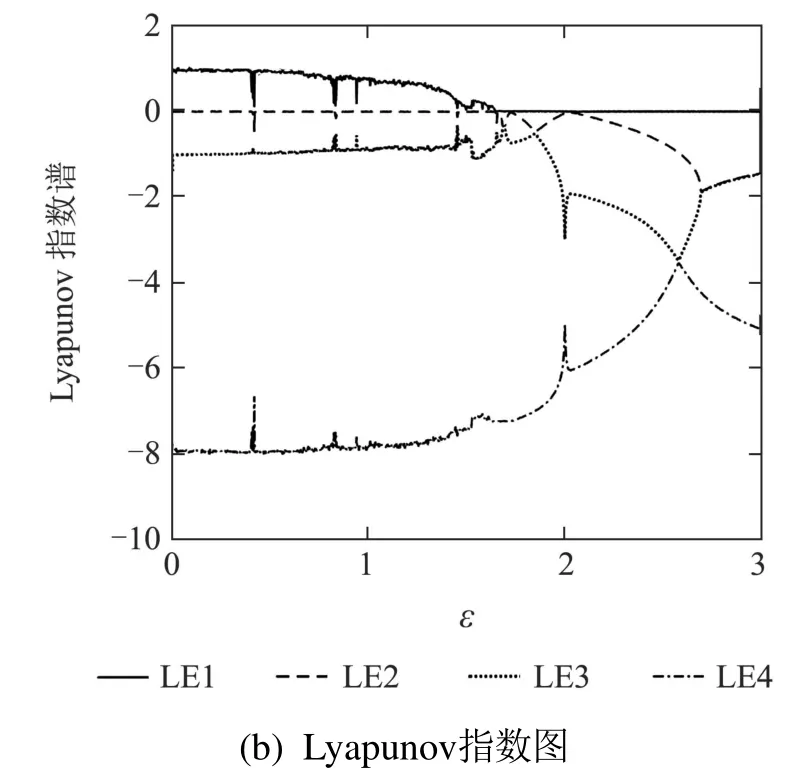
图9 系统(8)分岔图和Lyapunov指数谱Fig.9 Bifurcation diagram and Lyapunov exponent spectrum of system(8)

在控制的过程中系统的吸引域也会发生相应的变化,如图10所示.其中白色区域为无界解区域,图10(a)中黑色区域为系统(8)在ε=0(控制前)时可以产生四涡卷吸引子的吸引域,图10(b)中灰色区域为系统(8)在ε=2.4(控制后)时可以产生周期1极限环的吸引域.比较图10(a)和图10(b)可以发现,系统(8)的吸引域面积缩小,且集中在平衡点S2所在的区域.

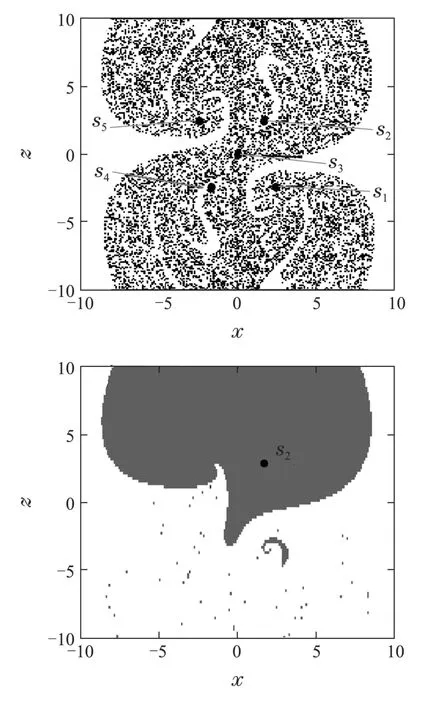
图10 系统(8)在控制前和后的吸引盆,取截面为y=u=0.1Fig.10 Basins of attraction of system(8)in y=u=0.1 plane before and after control

另外,当取q=x4=−1.6630时,可以得到相同的控制结果,只是最终剩下的平衡点为S4,最终的周期1极限环围绕平衡点S4如图11所示.

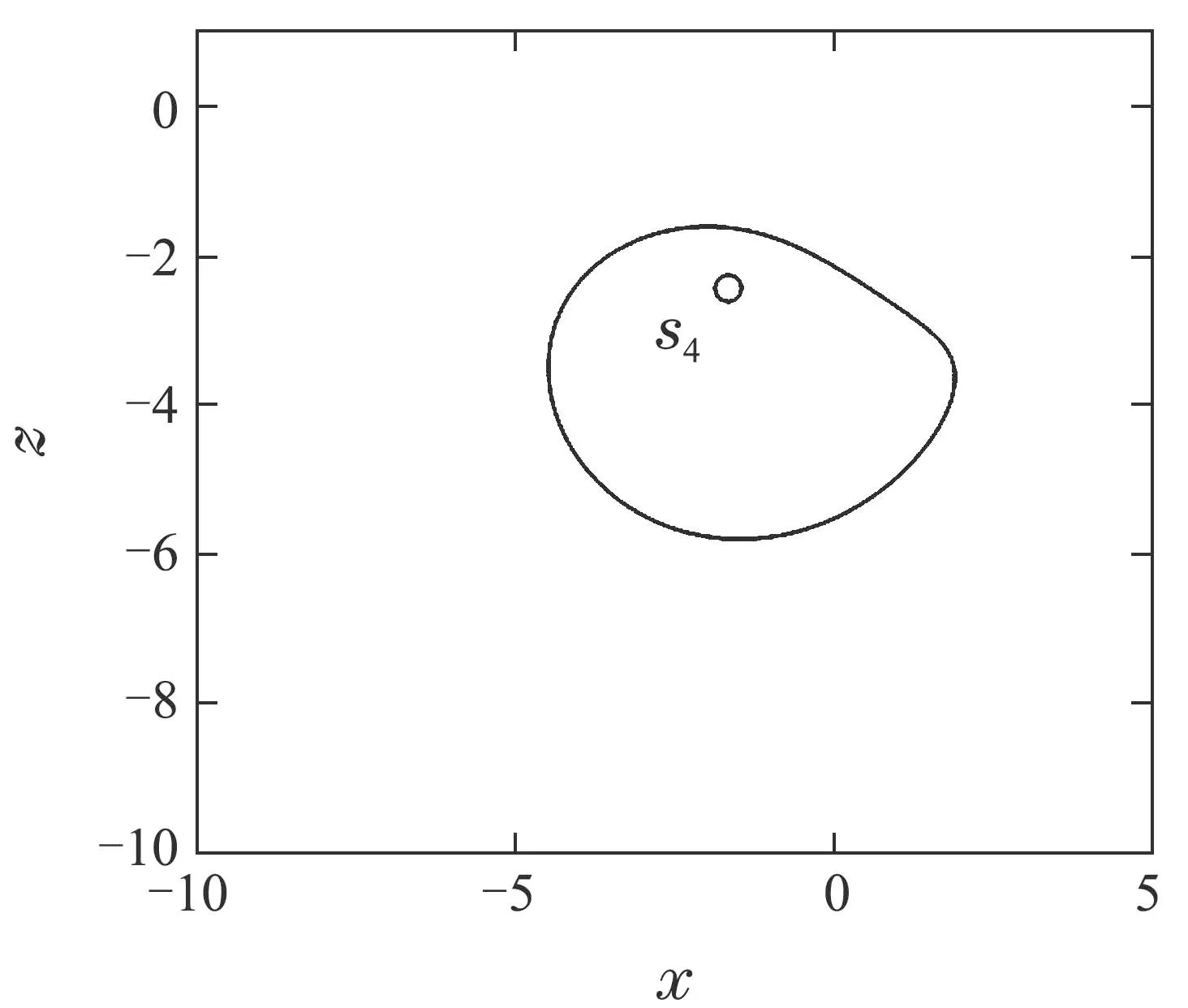
图11 q=−1.6630, ε=2.4,周期1Fig.11 period-1 limit cycle for q=−1.6630 and ε=2.4

5 四维风车型四翼吸引子系统

线性增量控制除了在不同涡卷数的三维系统中能够达到消除涡卷和抑制混沌的控制目标外,对于更高维数的多翼非线性系统一样适用.对一个四维四翼系统[23]进行改造得到一个可以产生风车型四翼吸引子的系统,引入线性增量控制后为

初始值条件为(1,1,1,1,0.1).通过不断增大耦合参数ε同样实现了蝶翼消除和混沌退化的控制目标,如图12中不同耦合参数ε下的相轨图所示.

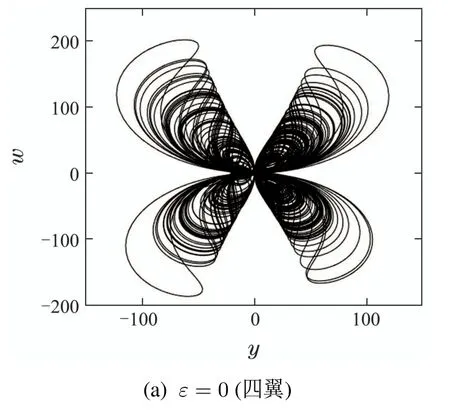
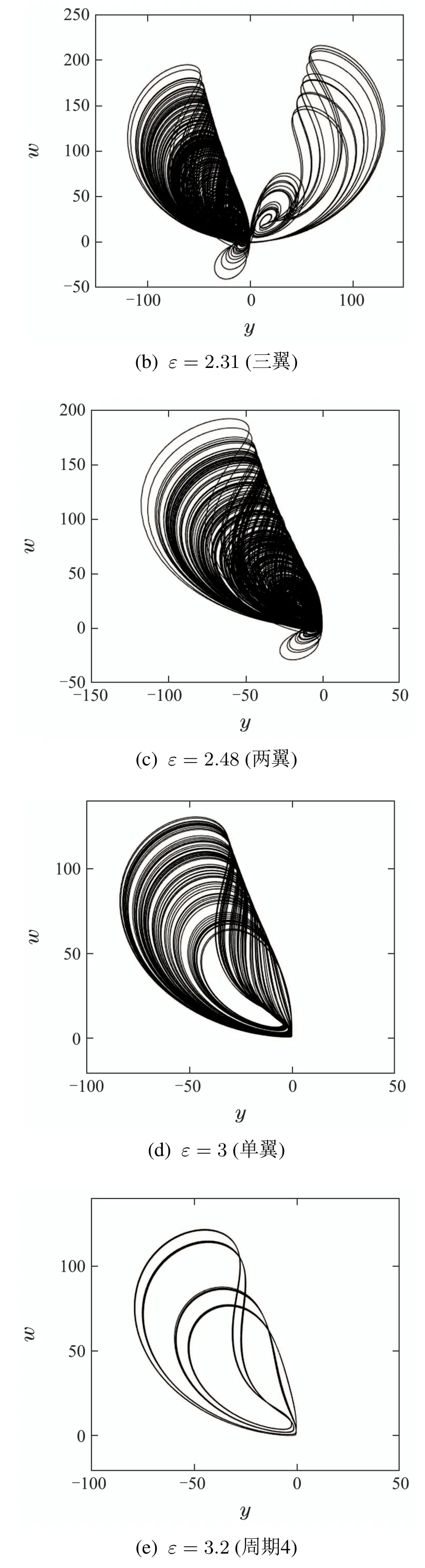
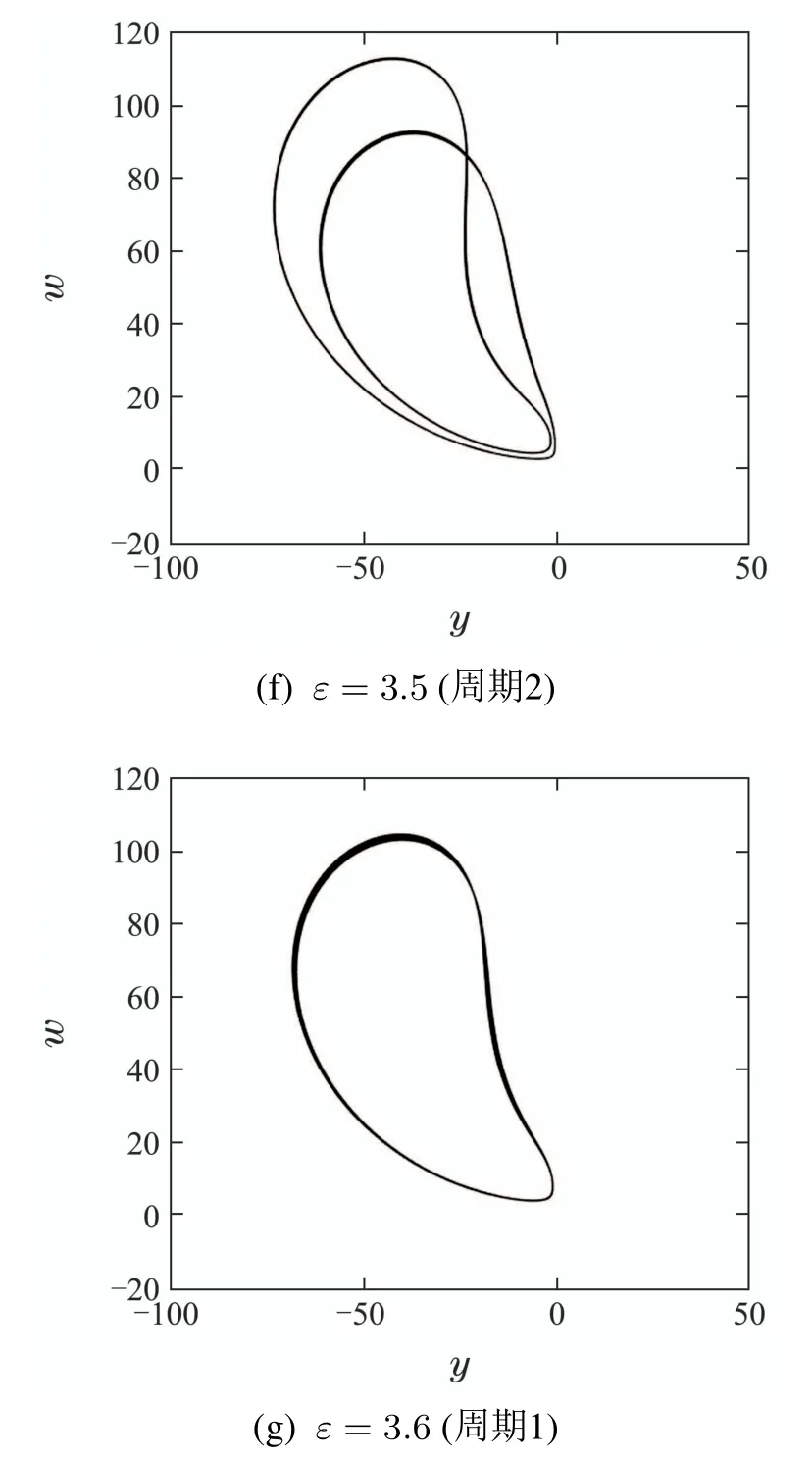
图12 系统(9)随耦合参数ε变化的吸引子在y–w平面的相轨图Fig.12 Phase portraits of attractor of the system(9)in the y–w plane under different values of ε

6 电路实现

以三维四翼吸引子系统的控制为例进行电路实现,设计的电路如图13中所示.为避免变量动态范围超出集成运放的线性动态范,在将系统(8)状态方程转换为电路方程时需将状态变量压缩10倍,而后进行时间尺度变换,时间尺度变换因子为τ0=1000.根据基尔霍夫定律,相应的电路方程可以描述为

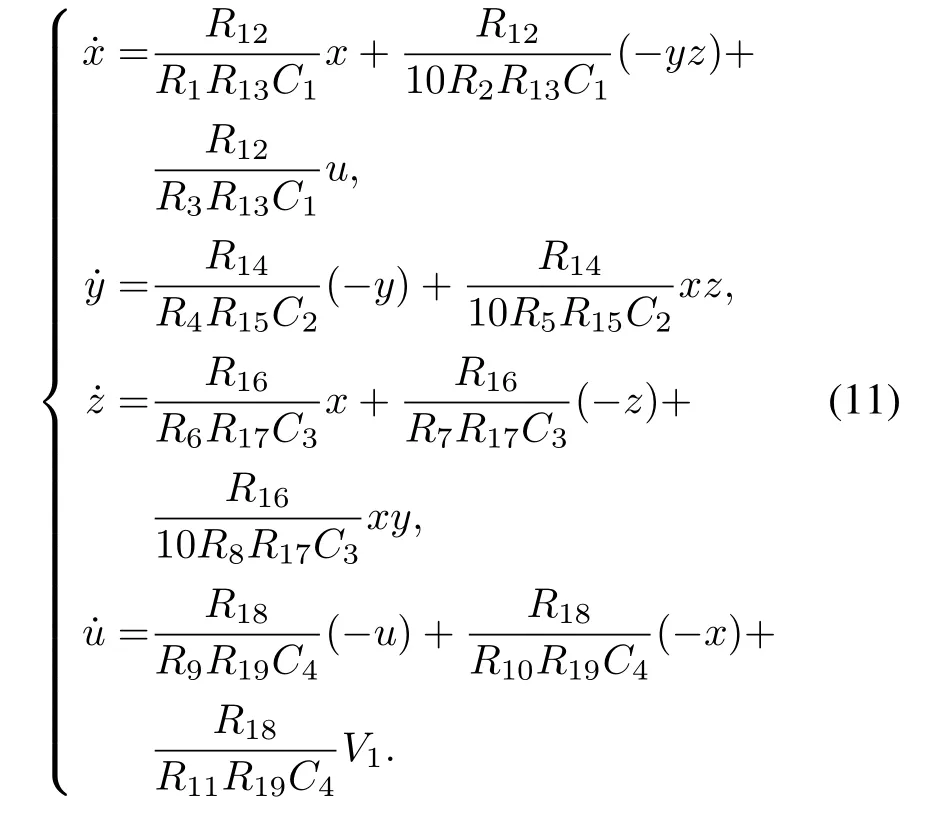
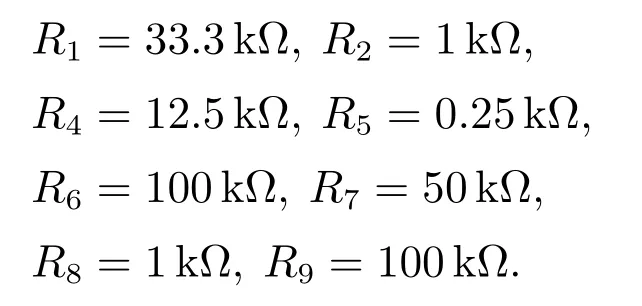
令R12至R19电阻值均为10 kΩ,电容值均为10 nF,通过计算可以得到通过调整R3,R10和R11三个电阻的电阻值即可得到在不同耦合参数ε下吸引子在x–z平面的相轨图,如图4所示.另外,为了验证该设计电路的实际可行性,搭建了硬件电路,如图15所示.在示波器上观测到的硬件电路实验结果与Multism仿真结果吻合,以四涡卷吸引子、单涡卷吸引子和周期1极限环为例,如图16所示.

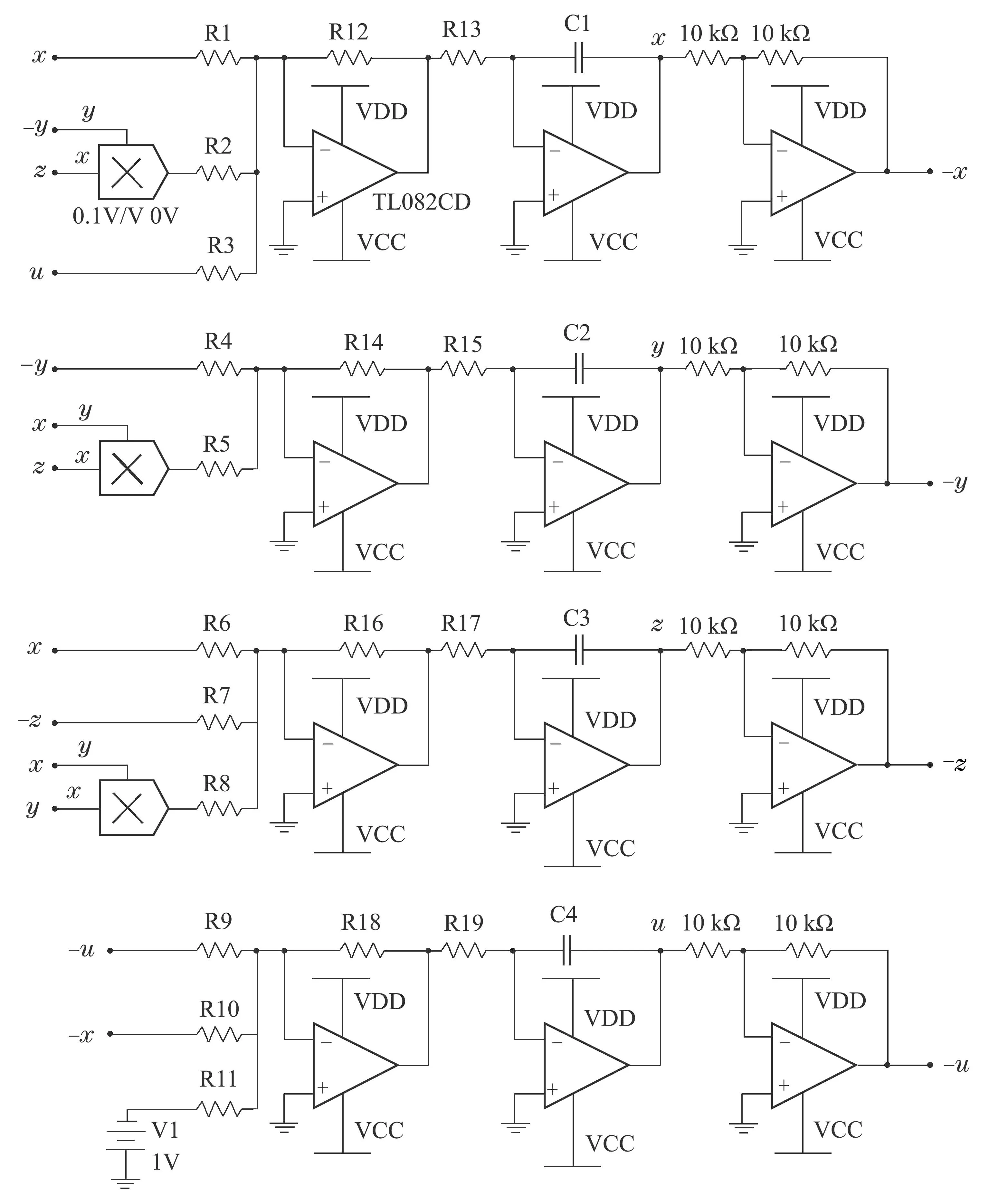
图13 系统(8)对应的电路图Fig.13 Chaotic circuit corresponding to system(8)

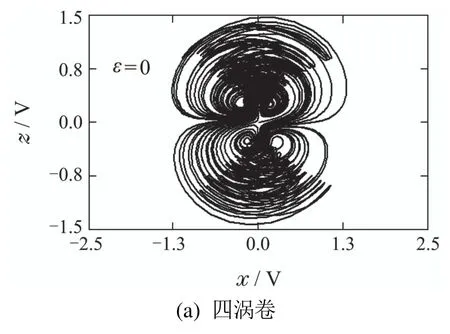
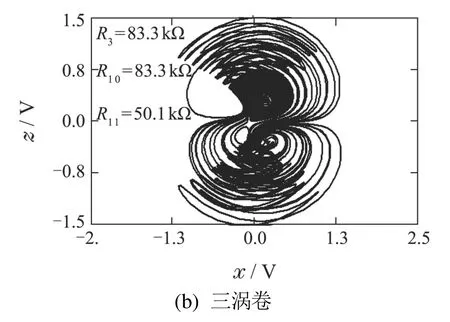
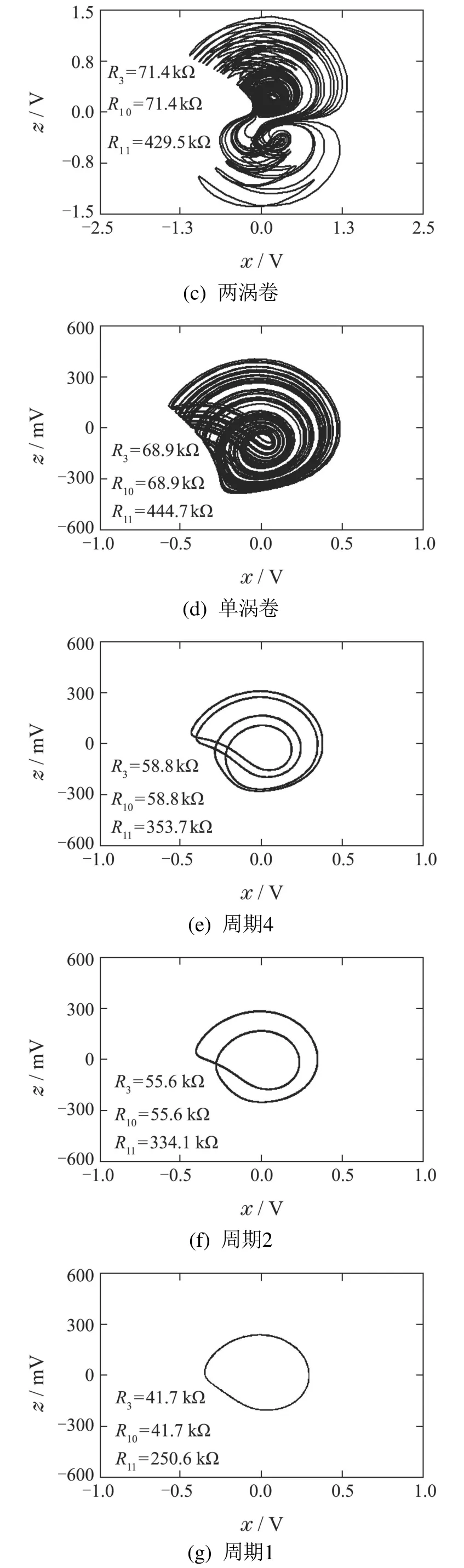
图14 Multism电路仿真结果Fig.14 Circuit simulation results captured on Multism

图15 硬件电路实验真实环境Fig.15 Real environment of hardware circuit experiment

图16 硬件电路实验结果Fig.16 Hardware circuit results captured in digital oscilloscope

7 结论

针对多涡卷非线性系统中吸引子简单化和混沌抑制的问题,本文证实了线性增量控制的有效性.三维Lorenz两翼吸引子系统、三维四翼系统以及四维风车型四翼吸引子系统作为被控制的例子,在x状态方程上引入了线性增量控制后,吸引子被退化且混沌被抑制.实际上,在其他不同维数不同涡卷数的多涡卷非线性系统中,引入此控制于任意状态变量方程上同样可以达到相同的控制效果.另外,线性增量控制电路结构简单,易于实现,仅通过调整受耦合参数影响的电阻的电阻值,即可实现在不同涡卷数的吸引子以及不同周期态之间灵活切换,将为混沌电路的控制提供一种实用方法.