武毅男,方勇纯,樊 志,王 超,刘存桓,胡子琦

(南开大学机器人与信息自动化研究所,天津 300350;天津市智能机器人技术重点实验室,天津 300350)

1 Introduction

As a powerful imaging and measuring instrument,an atomic force microscope(AFM)has been extensively used in materials[1],chemistry[2],life sciences and many other fields[3–4].An AFM has the ability to image,measure and manipulate samples at micro-nano scale with nanometer-scale accuracy[5].Meanwhile,it does not require special treatment for samples that preserves the original characteristics of samples[6],and enables observation and manipulation of samples in vacuum,atmospheric and liquid environments[7].Therefore,an AFM is reasonably expected to be applied to more practical scenarios[8–9].

Nevertheless,although an AFM has above-mentioned merits,its application is severely limited by the imaging range,since the drive unit of a commonly used AFM restricts its imaging field to the micron level[10].To compensate for this shortcoming,a common approach is to adopt such instruments with larger imaging range as an optical microscope(OM)to provide visual aid to an AFM[11].For this purpose,it is necessary to establish a confocal AFM system with an optical microscope,thus assisting AFM imaging by utilizing OM’s wide field of view[12].However,such confocal mode inevitably causes many problems when performing linkage control,positioning and imaging,since AFM and OM imaging ranges have cross-scale differences,that is,the imaging accuracy is nano-scale for an AFM and the imaging range of an AFM is micron-scale,while an OM has micron-scale imaging accuracy and centimeterscale imaging range[13].Therefore,it is necessary to figure out the corresponding location of an AFM image in the optical view by considering the difference between AFM and OM imaging,the key to which is to achieve the cross-scale registration for AFM and OM images.

For image registration,many studies have been carried out along with research results reported in the past years.For example,[14]reports an accurate,fast and robust method to correlate fluorescence microscope and electron microscope images using low densities of fducial markers.In addition,[15]presents a fast learningbased framework for deformable,pairwise medical image registration,which promises to speed up medical image analysis while facilitating novel directions in learning-based registration and its applications.Moreover,[16]proposes a simple yet surprisingly effective approach,termed as guided locality preserving matching,for robust feature matching of remote sensing images to achieve image registration.Besides,[17]introduces a fast geodesic shooting algorithm based on Fourier-approximated Lie algebras for diffeomorphic image registration.Moreover,[18]describes a method to infer voxel-level transformation from higher-level correspondence information contained in anatomical labels,which are more reliable and practical to obtain for reference sets of image pairs than voxel-level correspondence.

Although the above studies can achieve image registration,unfortunately,it is difficult to use existing methods to register AFM images in an optical image because of the different principles of AFM and OM imaging.More specifically,as a scanning probe microscope,an AFM utilizes the height information of the sample surface,obtained by probe scanning,to construct the image,so the brighter areas in the image represent the highland of the sample surface,while the darker areas correspond to the lowland of the sample surface.For an OM,because of its optical imaging principle,the brightness and darkness in the obtained image is irrelevant to the morphological height of the sample surface.Therefore,it is not feasible to directly perform image registration by utilizing gray scale information of AFM and OM images.

To solve the above issue,a cross-scale image registration algorithm based on geometric feature similarity evaluation is proposed for AFM and OM images in this paper.In particular,the relationship between AFM and OM imaging scales is first calibrated with using the specific geometric pattern imprinted by an AFM probe.Furthermore,a practical image processing algorithm is designed to effectively extract the geometric feature in AFM and OM images.Moreover,based on the proposed geometric feature similarity evaluation function,a novel cross-scale image registration algorithm is developed to accurately position the AFM image in the optical field of view,which therefore achieves registration for AFM and OM images,thus providing a powerful basis for further implementing linkage control and imaging of the confocal AFM and OM system.

The remainder of the paper is organized as follows:Section 2 analyzes the difficulty of image registration between an AFM and an OM.In Section 3,the implement process of the novel geometric feature based image registration algorithm is presented to elaborate the technique.Section 4 provides the convictive experimental results to verify the superior performance of the proposed method.The conclusions of the paper are made in Section 5.

2 Problem analysis of image registration between AFM and OM

An AFM adopts a probe to detect the sample surface,and the tiny force between the probe tip and the sample is controlled by a feedback mechanism to keep constant during the scanning process,which ensures the constant distance between the probe tip and the sample surface[20],thereby resulting in the fact that the vertical displacement of the probe is able to reflect the morphological height of the sample[19].Based on the operating principle of an AFM,the morphological image of the sample is drawn by using the height data of the sample surface[21].Hence,the gray scale values of an AFM image are determined by the sample surface morphology,that is,the brighter areas in an AFM image correspond to the highlands of the sample surface,while the darker ones denote the lowlands of the sample surface[22].

In addition,different from the imaging principle of an AFM,images captured by an optical microscope are observed from eyepiece and further stored by a charge coupled device(CCD)camera[23].A CCD camera is capable of forming a strong or weak charge on each capacitance unit by capturing the intensity of the light,thus converting optical images into digital signals.Therefore,the gray scale values of an optical image are determined by the intensity of the light,and cannot reflect the morphological height of the sample surface[24].

To further illustrate the above issue,an AFM image of HeLa cells is shown in Fig.1(a),while the corresponding optical image is presented in Fig.1(b).For the AFM image,the size is 30 µm×30 µm,and the color bar of the AFM image indicates that the higher the brightness of the area,the higher the corresponding morphology of the sample surface.However,for the optical image,the brighter areas correspond to substrate,and the dark circular areas denote HeLa cells with higher morphological height than that of the brighter areas,which are exactly different from the meaning of the brightness in the AFM image.Besides,it can be seen from the two images that,there is a huge difference between the AFM and OM imaging scales.Therefore,it is difficult to achieve the registration between AFM and OM images by directly using gray scale information of the images.

3 Image registration algorithm design based on geometry similarity evaluation

To solve the above problem,in this paper,a geometric feature similarity evaluation algorithm is proposed to achieve cross-scale image registration between AFM and OM images.To be specific,because of the difference in imaging scales between an AFM and an OM,it is necessary to first perform scale calibration for further achieving cross-scale image registration.Since scale calibration requires a calibrator that is suitable for both AFM and OM imaging,the specific geometric pattern is imprinted on the surface of a flat transparent sample and then imaged by an AFM and an OM.Based on the imaging results,the relationship between the imaging scales of the two microscopes is calibrated to provide the basis for image registration.Furthermore,since these two microscopes differ significantly in imaging principles,it is infeasible to directly adopt existing methods to implement image registration.Therefore,a geometric similarity evaluation method is necessary to be proposed for image registration with high accuracy.For this purpose,the geometric feature of the images needs to be accurately extracted for further similarity assessment,hence,an effective image processing algorithm is designed to extract the geometric feature of the AFM and OM images,which is then combined with the calibrated scale to generate inner angle vectors and side length vectors.Based on the quantized geometric feature,an advanced similarity evaluation function is proposed to accurately register the AFM image in the optical imaging result,thus achieving cross-scale image registration between an AFM and an OM.The Flow chart of the proposed method is illustrated in Fig.2.

Fig.1 AFM and OM imaging results of HeLa cells

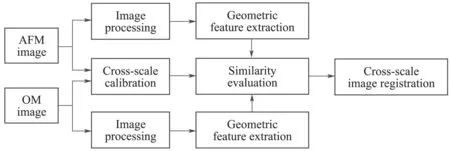
Fig.2 Flow chart of the proposed algorithm

3.1 Cross-scale calibration based on geometric pattern imprint

Due to the difference between AFM and OM imaging scales,it is necessary to first calibrate the specific proportional relationship between imaging scales to facilitate image registration.When performing scale calibration,it is important to select or produce a suitable calibrater with exact size.By comprehensively considering the scales and principles of AFM and OM imaging,the calibrater needs to be micron-sized for both AFM and OM imaging,besides,it is better to be transparent to facilitate OM imaging.Based on the above analysis,a petri dish is selected to be imprinted with specific geometric pattern by an AFM probe to produce a micron-sized calibrater,since it is transparent and has flat surface with hardness adapted to be imprinted.More specifically,the imprint process is implemented by an AFM,in a specified rectangular area,the force,applied by the probe to the sample surface,is increased by changing the set point of the distance between the probe and the sample surface,so as to conduct imprint on the sample surface.The imaging results of the imprinted sample are shown in Fig.3,where Fig.3(a) presents the AFM imaging result,and the dark square area denotes the imprinted result with the size of L×L.The imaging result of an OM is shown in Fig.3(b),where the imprint in the blue dashed square frame corresponds to the dark square area in Fig.3(a).

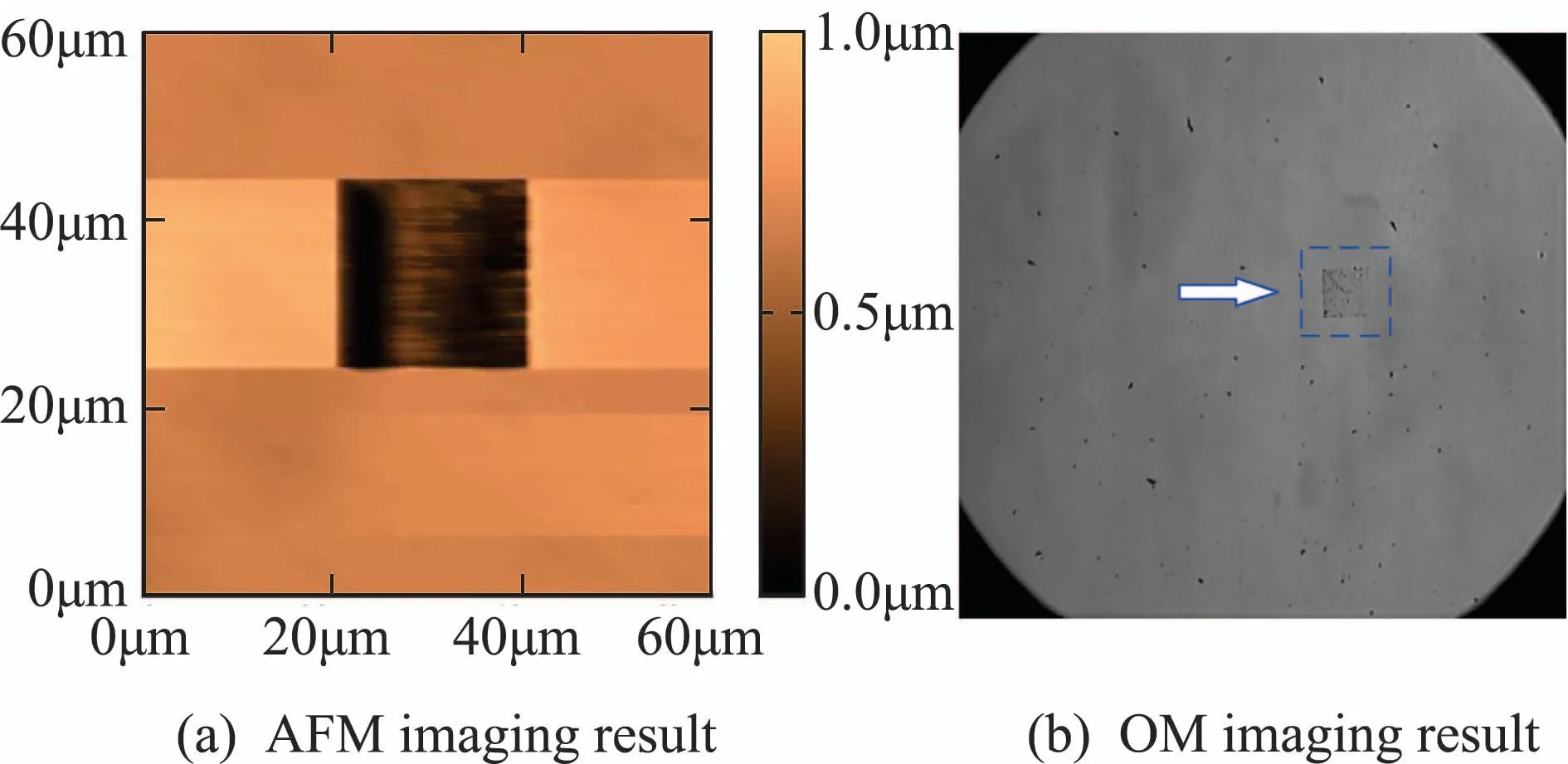
Fig.3 AFM and OM imaging results of the imprinted sample

After obtaining the imaging results of the imprinted sample,assume that the optical microscope uses k× magnification,the calibration is implemented by utilizing the correspondence between pixels and dimensions as follows:

where SAFMand SOMdenote the actual size of each pixel in AFM and OM imaging results,respectively.L represents the actual side length of the imprinted square area. NAFMand NOMstand for the number of pixels in the imprinted area in AFM and OM images,which are crucial to implement the cross-scale calibration.To obtain the accurate values of NAFMand NOM,the AFM and OM images are first processed by Gaussian filtering and then binarized by OTSU algorithm to separate the imprinted area from the background.In the binary images,the gray values of the pixels in the imprinted area are set to 1,while those in the other area are set to 0.Therefore, NAFMand NOMare calculated by counting the number of pixels with the gray value as 1.

Therefore,the cross-scale calibration between AFM and OM images is performed by calculating the proportional relationship of imaging scales:

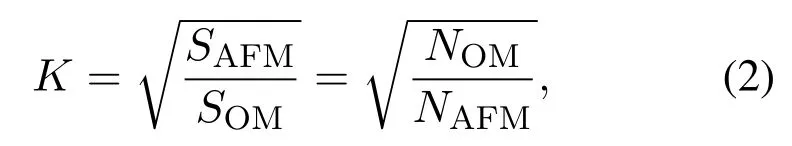
where K denotes the scale ratio between OM and AFM imaging results when the OM adopts k×magnification to image.

3.2 Geometric feature extraction based on image processing

To better achieve image registration,the petri dish is imprinted with multiple rectangles in the same manner as described above,the centroids of the rectangles thus constitute a geometric pattern that can be used as a template for image registration.Fig.4 shows four kinds of imprinted results with different geometrical shapes,where Figs.4(a)–4(d) present line,triangle,quadrangle and polygon,respectively.

After completing the imprint on the sample surface with geometric patterns,it is important to accurately extract the geometric feature of the image by adopting an appropriate algorithm,so as to provide a strong guarantee for subsequent image registration based on geometric feature similarity.Therefore,an effective image processing algorithm is designed to be applicable to geometric feature extraction for both AFM and OM images.To be specific,to extract the geometric feature of the imprinted sample,the AFM image is first filtered to eliminate the noise,the result of which is then performed image binarization to make the imprint easy to extract.Afterwards,the locations of the imprinted areas in the binary image are obtained by eight neighborhood connectivity algorithm,based on which the centroid of each imprinted area is calculated to construct a geometrical shape,thus achieving geometric feature extraction for the AFM image.The flow chart of the geometric feature extraction with image processing is shown in Fig.5.

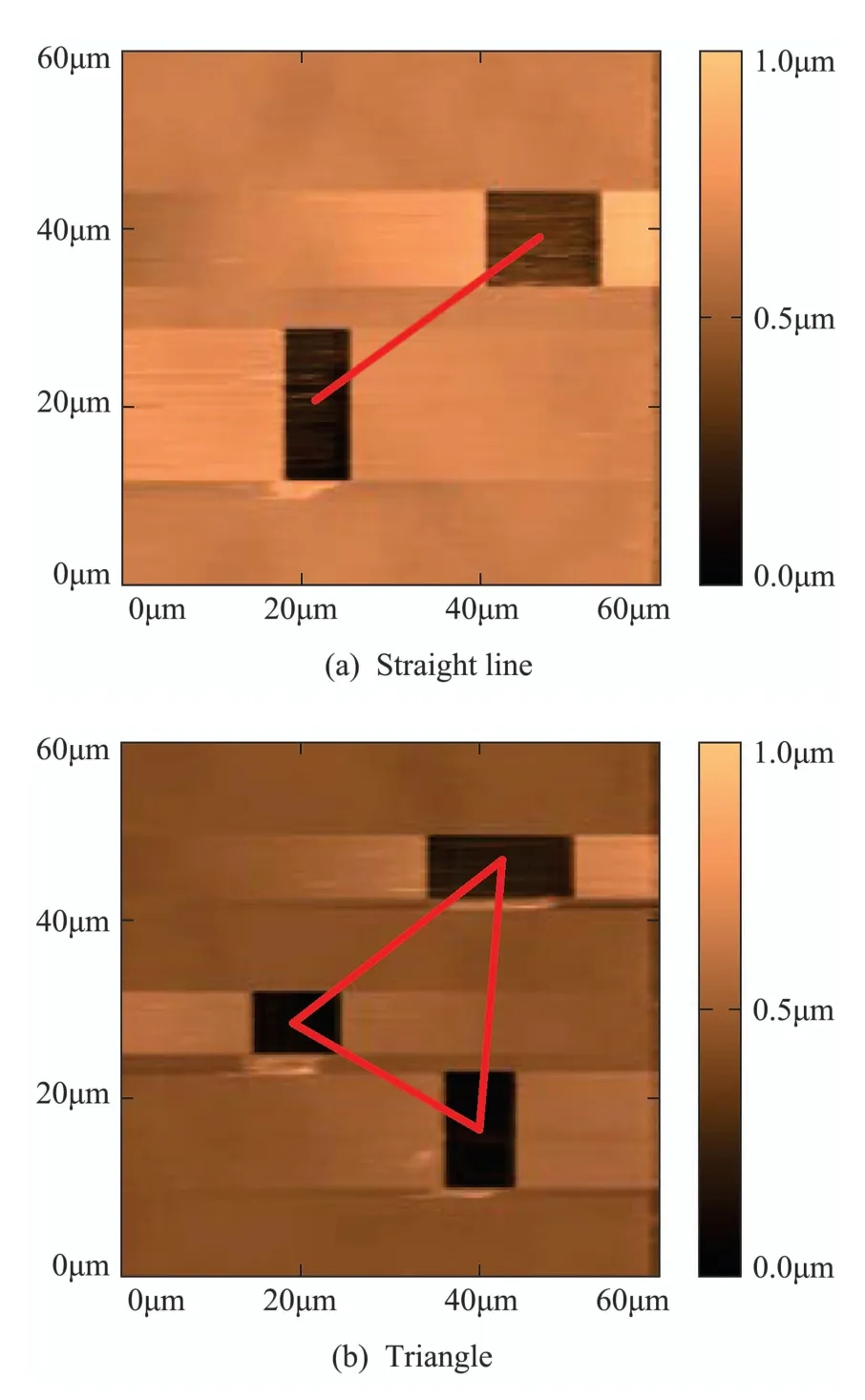
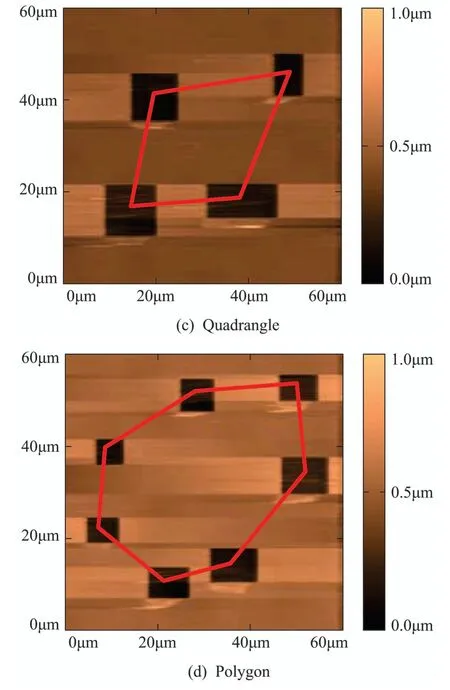
Fig.4 Four kinds of imprinted results with different patterns

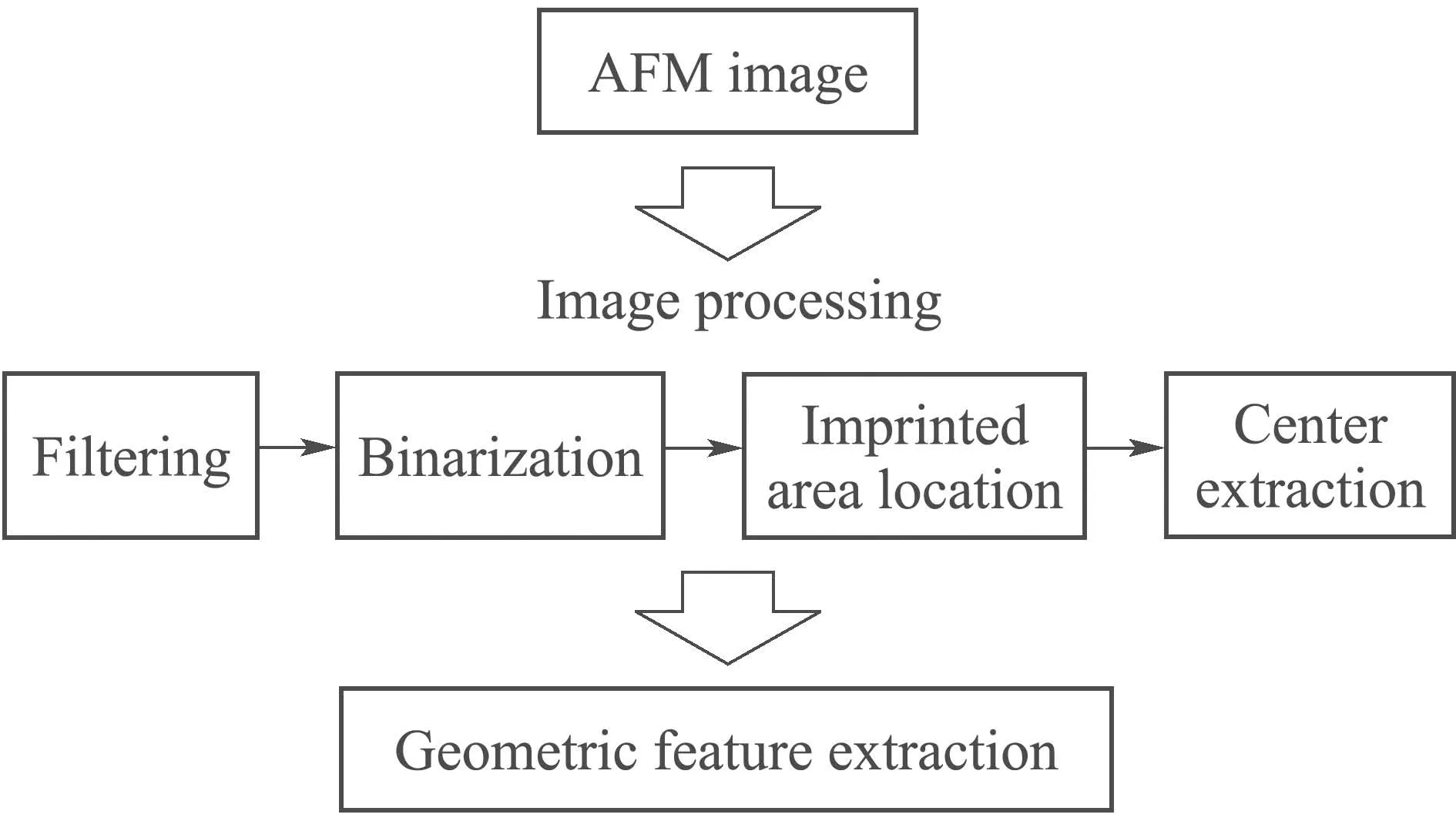
Fig.5 Flow chart of the geometric feature extraction

To be specific,since a bilateral filter introduces a spatial distribution Gaussian function to preserve true gray values near the edges[25],it is first adopted to remove image noise while guaranteeing not to impair the sharpness of the edges with the result shown in Fig.6(a),thereby contributing to subsequent image binarization and object location.Then,the filtered image is binarized by OTSU algorithm to adaptively separate the imprinted areas from the background[26],the binarization result is presented in Fig.6(b),where the white areas correspond to the imprinted results.Afterwards,the image is processed by eight neighborhood connectivity algorithm to obtain the locations of the white connected areas in the image,and the image centroid of each connected area is calculated as follows:

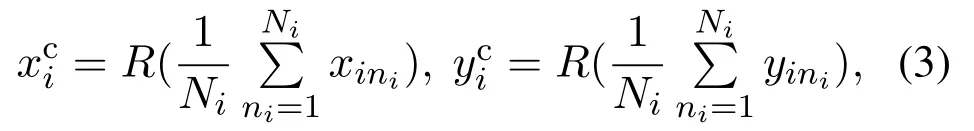
Afterwards,based on the position information of the extracted centroids,the geometric feature is quantized into an interior angle vector and a side length vector to facilitate the subsequent similarity calculation of geometric feature.The two vectors are constructed to store geometric feature as follows:

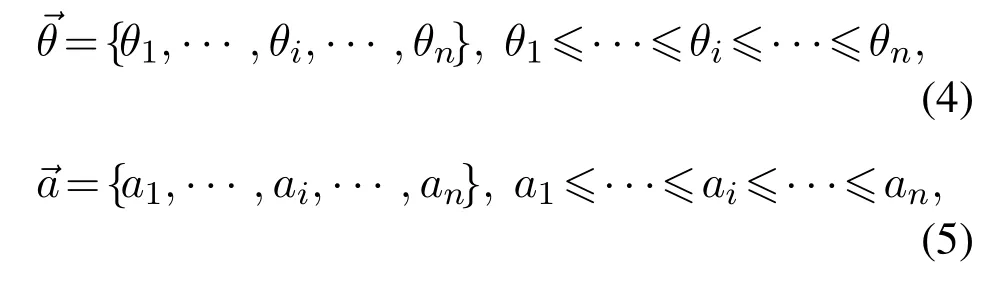
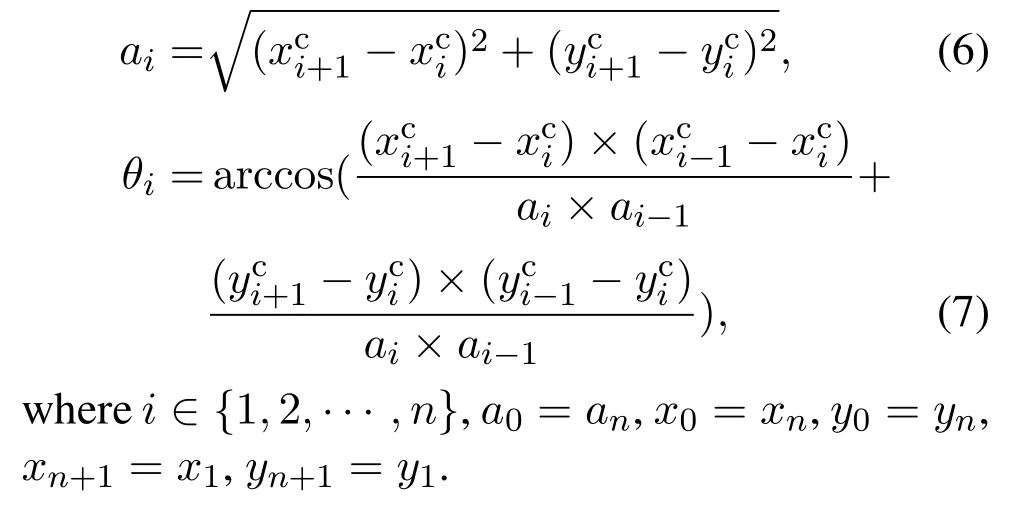
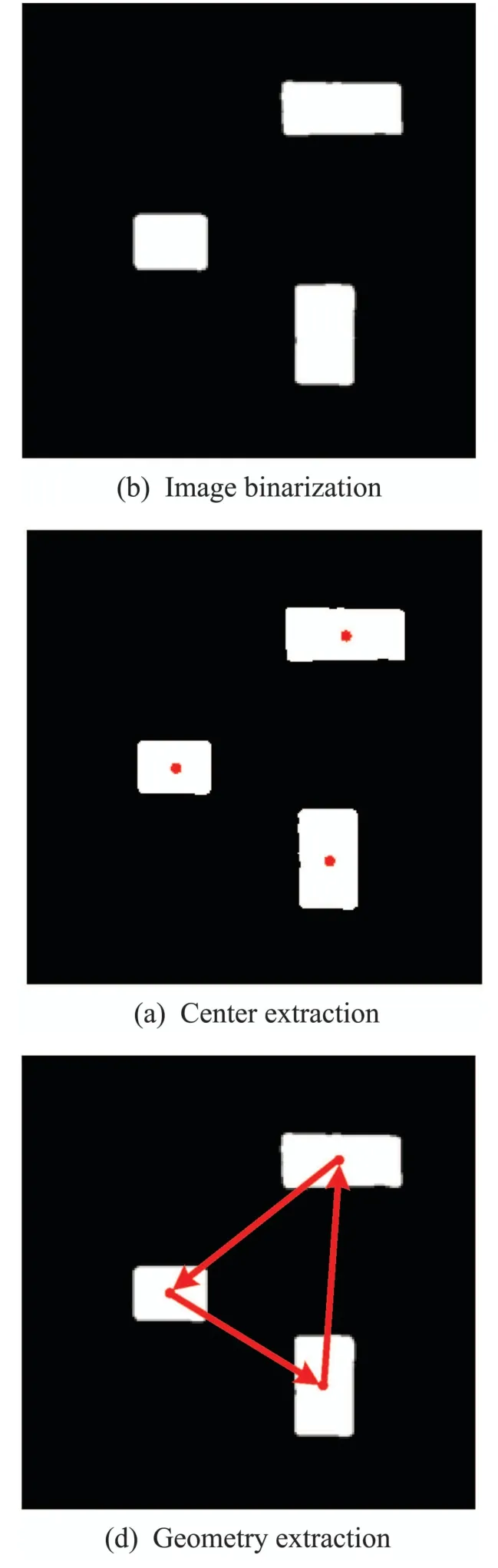
Fig.6 The result of geometric feature extraction

3.3 Cross-scale image registration based on geometry similarity evaluation

Based on the extracted geometric feature,the image registration is implemented by sliding matching while considering the imaging scale ratio.Since the final image registration is determined by the similarity evaluation results in different sliding regions,it is pivotal to design a similarity evaluation function with high accuracy and efficiency.Therefore,in this section,an advanced geometric feature similarity evaluation function is proposed to accurately achieve crossscale image registration.To be specific,for an optical image obtained at k× magnification of an OM,the length vectorof the AFM image needs to be transformed as follows:

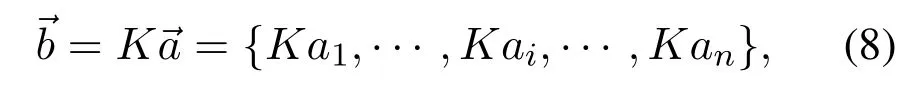
thus eliminating scale difference between AFM and OM images to facilitate image registration.Furthermore,andare utilized for sliding matching,and the size of the sliding window is determined as follows:

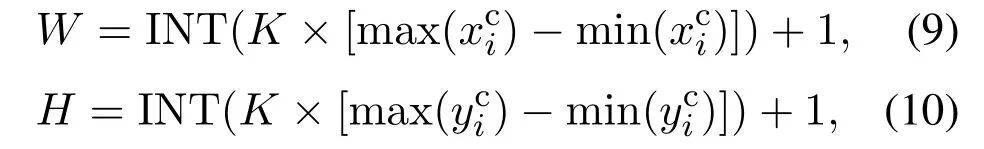
where W and H denote the width and height of the sliding window,respectively,INT(·) is an integervalued function to generate the largest integer that does not exceed the real number,max(·)and min(·)represent the maximum and minimum functions.

For each region with the size of W × H in the optical image,its geometric feature is extracted with the same method as that for the AFM image,of which two vectors are also generated as follows:

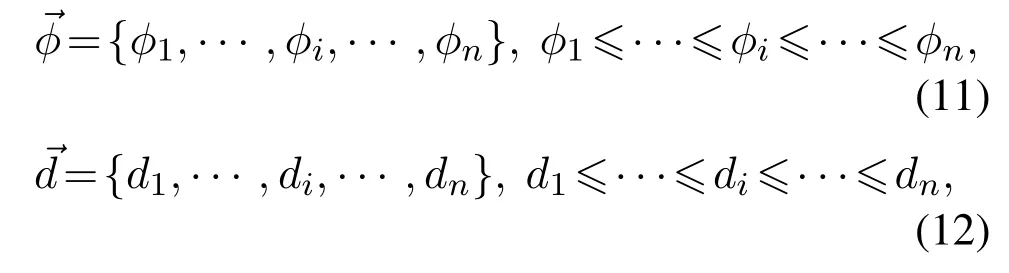
Moreover,the sum of the inner angles of the geometry,extracted from the AFM image,is first to be compared with that in the sliding window area of the OM image.The type of geometry is different in the two images when the sum of the inner angles is different,which implies that the AFM image is not matched to the current sliding window area of the OM image.In this way,there is no need to further judge the similarity of the geometries when the sum of the inner angles is different,thereby improving the efficiency of image registration.Therefore,a judgment function about the sum of the inner angles is constructed as follows:

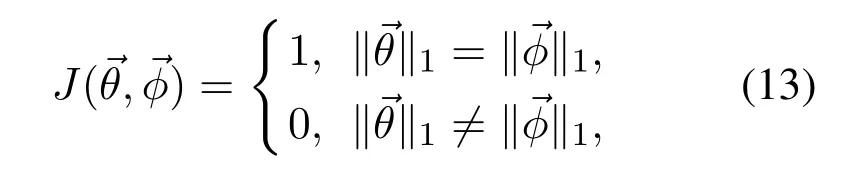
where ‖·‖1denotes 1-norm that is the sum of absolute values of vector elements.

Furthermore,a geometry similarity evaluation function is designed as follows:

where F(·)∈[0,1],and it implies that the image registration is successful when the value of the evaluation function is close to 1.

4 Experiments and Analysis

In the experiments,the proposed algorithm is applied on a confocal AFM system with an optical microscope.The confocal system is shown in Fig.7,which includes a light source,an Andor CCD camera,a Nanosurf Flex–FPM AFM and a Nikon Eclipse Ti inverted optical microscope.

Fig.7 The confocal AFM system with an optical microscope

To fully verify the performance of the proposed image registration algorithm,four kinds of imprints on a petri dish with different geometrical shapes,namely straight line,triangle,quadrangle and polygon,are used to generate the corresponding AFM and OM images to implement image registration.The calculation time of image registration for different patterns is 167.3 s for straight line,175.6 s for triangle,189.3 s for quadrangle and 217.2 s for polygon.The configuration of the computer used for image registration is Intel(R)Core(TM)i5–2400 CPU@3.10 GHz with the memory of 4 GB.The results of image registration are presented in Fig.8,where the optical image is obtained by the OM at 40× magnification,the actual size of the AFM image is 60µm×60µm,and the weights of the image registration evaluation function are set to:ω=0.5, ρ=0.5.Fig.8(a)presents the image registration areas in the optical image for the four kinds of geometric patterns according to similarity evaluation results of the proposed method,where the optical images inside the red frames are the areas extracted by the proposed image registration algorithm for different geometric patterns.To further visualize the image registration results,Figs.8(b)–8(e)show the geometric feature for the four kinds of patterns in the AFM images and the registration results of the OM images,where the tagged angles correspond to the angles of the inner corners of different geometric patterns which are obtained by the designed image processing algorithm.It can be seen intuitively from the results that,the four AFM images with different geometric patterns are accurately registered into the optical image,thus demonstrating the satisfactory performance of the proposed cross-scale image registration algorithm.

To further elaborate the calculation process of image registration,the similarity calculation results for four kinds of geometrical shapes are exhibited in Table 1,including the specific results of inner angle vectors and side length vectors.To be specific,for the geometry of straight line,the sum of the inner angles is 0◦for both the AFM and OM images,and the similarity of the registered images is calculated as 1.0000.For the geometry of triangle,the sum of the inner angles is 180◦for the AFM and OM images,and the similarity is 0.9999.For the geometry of quadrangle,the sum of the inner angles is 360◦for the AFM and OM images,and the similarity is calculated as 0.9998.For the geometry of polygon,the sum of the inner angles is 900◦for the AFM and OM images,and the similarity is 0.9922.In summary,the similarity calculation results for the four geometries are close to 1,which further verifies that the proposed algorithm enables high precision image registration.

Furthermore,to verify the advantages of the proposed method over other image registration methods,two classic similarity evaluation methods,namely structural similarity index measure (SSIM) and histogram similarity measure (HSM),are selected for comparison experiments with the proposed one,so as to fully demonstrate the effectiveness of the proposed method in the paper.SSIM comprehensively analyzes and calculates image brightness,contrast and structure from the perspective of image composition[28],so that the similarity of two images can be evaluated within the range of[0,1].As another widely used image similarity evaluation method,HSM is performed by calculating the normalized correlation coefficients of the histograms of two images[29],so as to evaluate the similarity of the images within the range of[0,1].For these two methods,the more similar the two images are,the closer the similarity calculation result is to 1,and the similarity calculation result is equal to 1 when the two images are exactly the same.Due to the effectiveness of SSIM and HSM,in many related studies,these two methods are suitable for comparative experiments to better demonstrate the performance of some novel methods[30–31].

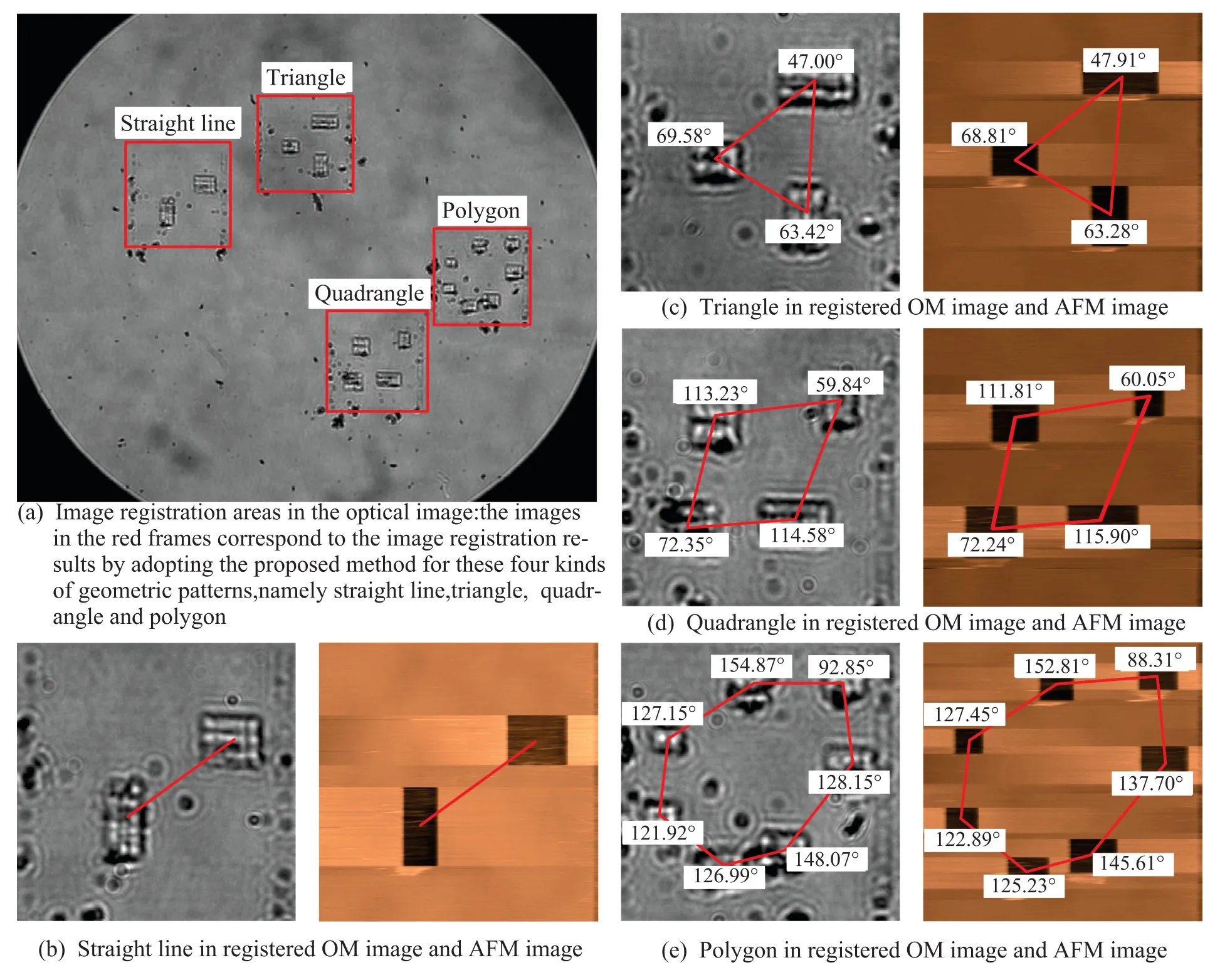
Fig.8 Image registration results of the proposed method for the four kinds of geometric patterns

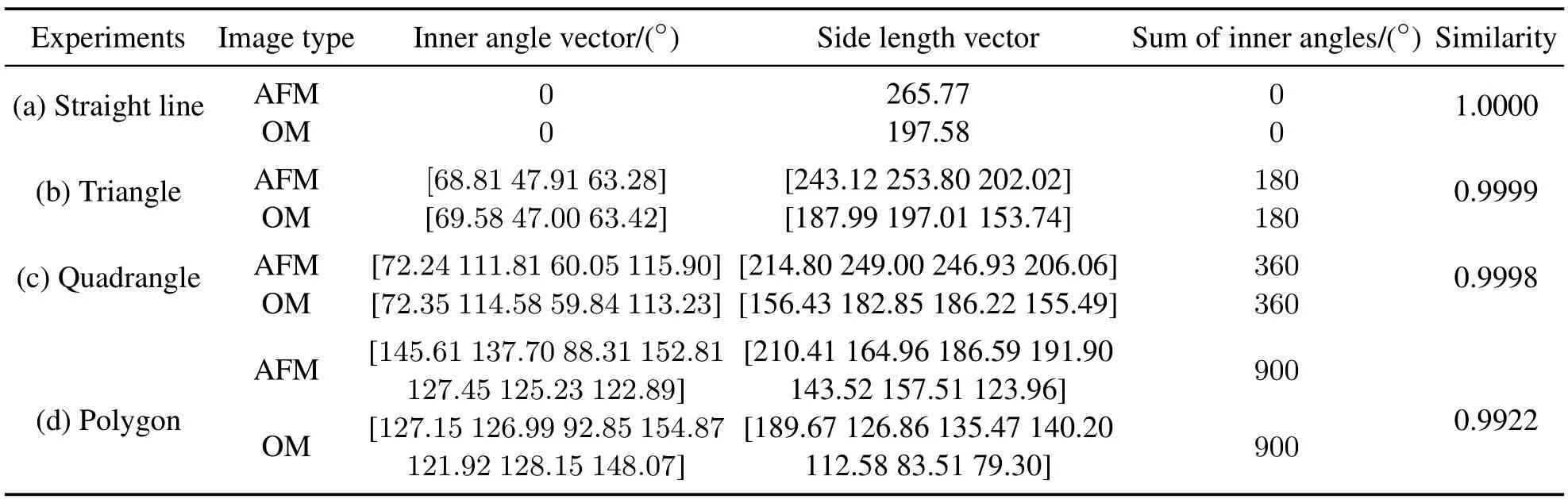
Table 1 Similarity calculation results for four kinds of geometrical shapes

The experimental results of these two methods are shown in Fig.9,where the optical images in the blue dashed frames are the registration areas obtained by using SSIM,and the optical images in the yellow dotted frames are the registration results of HSM.The image registration results of these two methods are both incorrect compared to the correct areas in the red solid frames in Fig.9 obtained by the proposed method.

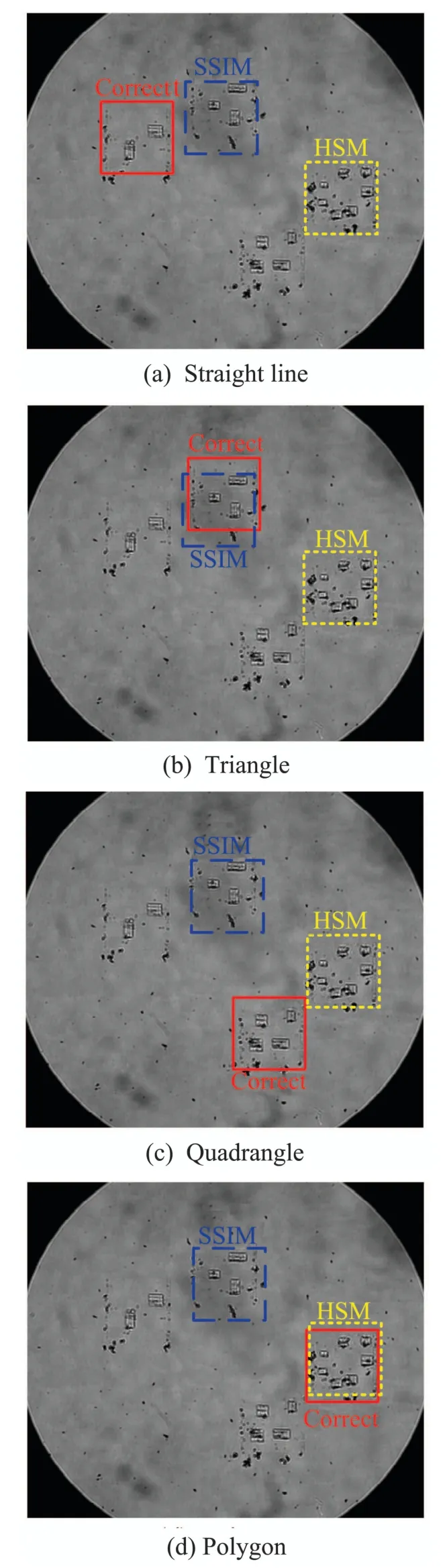
Fig.9 Image registration results of SSIM and HSM for the four kinds of geometric patterns

Meanwhile,the similarity calculation results of these two classic methods for different geometric patterns are presented in Table 2.For the method of SSIM,the image registration is implemented by determining the area with the maximum similarity in the optical image as the registration result,and the similarity calculation results of the image registration areas for the four patterns are 0.9553,0.9495,0.9423 and 0.9456.However,the similarity calculation results of SSIM for the correct areas in the red solid frames are 0.9493,0.9455,0.9365 and 0.9401,which lead to the inability to find the correct registration areas since the image registration is determined by the maximum value of the similarity calculation result,thereby verifying that SSIM is not suitable for cross-scale registration between AFM and OM images.Similarly,for the method of HSM,the maximum similarity calculation results for the four patterns are 0.1189,0.1752,0.2191 and 0.2317,which determine the registration results as shown in the yellow dotted areas in Fig.9,while the similarity for the correct registration areas in the red solid frames are calculated as 0.0947,0.1679,0.2076 and 0.2297 by using HSM,which lead to the incorrect registration results of HSM.It can be seen from the registration results of HSM that,it is not suitable for AFM and OM image registration by directly using gray scale information to perform similarity evaluation.Therefore,the comparative experiments indicate that these two classic image similarity evaluation methods are not suitable for cross-scale image registration between AFM and OM images because of the different principles of AFM and OM imaging.

5 Conclusions

This paper proposes a novel cross-scale image registration algorithm for AFM and OM images.To be specific,geometric pattern imprint is first implemented to achieve the scale calibration for AFM and OM imaging.Afterwards,the imprinted samples are used to generate AFM and OM images,and the geometric feature is then extracted by the designed image processing algorithm,which provide the basis for accurate image registration.Furthermore,an advanced geometric feature similarity evaluation function is proposed to accurately register the AFM image in the optical image,therby achieving the crossscale image registration.Experiments and analysis are provided to demonstrate the good performance of the proposed method.Future work will focus on the implementation of linkage control and positioning for the confocal AFM system with an OM based on the proposed algorithm in this paper.

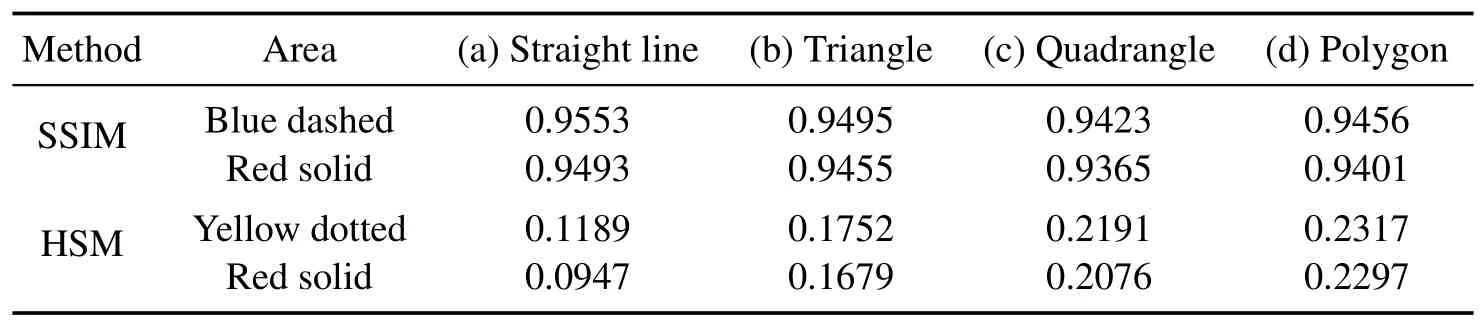
Table 2 Similarity calculation results of SSIM and HSM for different geometric patterns