徐伟建 李云萍

摘  要：“一课一题”具有切口小、针对性强的特点，是深受师生喜爱的小专题复习课型. 文章以一道中考压轴题为载体，从不同的提问角度设计案例，展示“一课一题”的设计思路与方法，体现系统架构、整体设计、拾级而上的教学理念，培养学生的数学学科核心素养，促进教师专业发展.

关键词：中考试题;一课一题;教学设计

笔者曾在一次名师工作室开展的“一课一题”教学研讨活动中，要求教师根据所给的一道中考压轴题，以“一课一题”的形式进行教学微设计. 大家在剖析试题立意，挖掘问题内涵，架构知识体系上下工夫，设计出多个“一课一题”教学微案例，现做整理，供大家研讨参考.

一、试题呈现

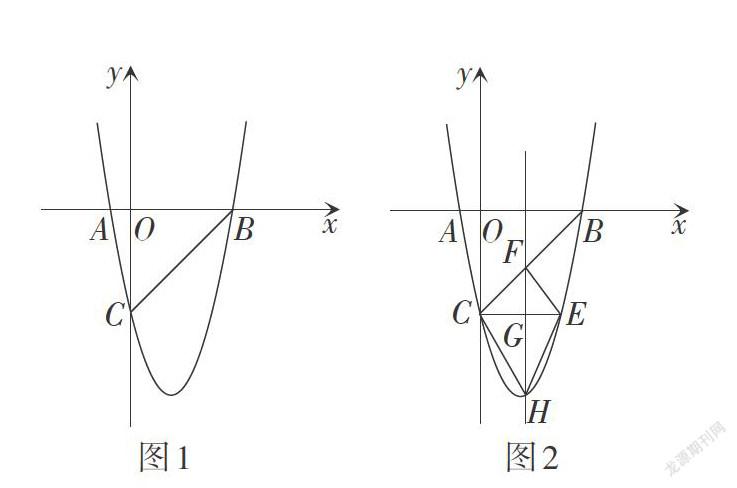
题目 （2017年湖南·怀化卷）如图1，在平面直角坐标系中，已知抛物线[y=ax2+bx-5]与x轴交于[A-1，0，] [B5，0]两点，与y轴交于点C.

（1）求抛物线的函数表达式;

（2）若点D是y轴上的一点，且以B，C，D为顶点的三角形与[△ABC]相似，求点D的坐标;

（3）如图2，[CE∥Ox]与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC，CE分别相交于点F，G，试探究当点H运动到何处时，四边形CHEF的面积最大，求点H的坐标及最大面积;

（4）若点K为抛物线的顶点，点[M4，m]是该抛物线上的一点，在x轴，y轴上分别找点P，Q，使四边形PQKM的周长最小，求出点P，Q的坐标.

【评析】该题的4道小题分别是：求二次函数表达式;特征几何图形（相似三角形）存在性;动态四边形面积的最大值;利用“将军饮马”模型求四边形周长的最小值. 除了第（1）小题较为基础，第（2）（3）（4）小题层层递进，且都有一定的综合性，蕴涵着众多数学知识和思想方法，对一般学生而言并非一蹴而就.

本文基于对学情的分析，以题目的4道小题为切入点，依据“系统架构、整体设计、拾级而上”的思路，设计出以下“一课一题”教学微设计案例，运用于二次函数小专题复习.

二、設计案例

案例1：从梳理二次函数基础知识进行设计.

原题第（1）小题是求抛物线的函数表达式，属于二次函数的基础知识. 众所周知，二次函数的性质丰富、运用广泛. 因此，将二次函数的重要性质与思想方法进行系统梳理，并融入该抛物线背景中，可以设计二次函数基础复习课.

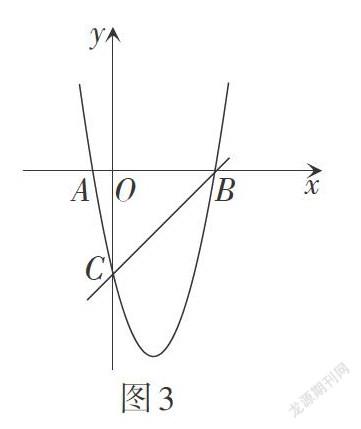
如图3，在平面直角坐标系中，已知抛物线[y=ax2+][bx-5]与x轴交于[A-1，0，B5，0]两点，与y轴交于点C.

问题1：求抛物线的函数表达式.

问题2：结合函数的图象，写出该函数的几条性质.

【评析】问题2属于开放式设计，“以题带点”让学生自主梳理二次函数的基本性质，如开口方向、顶点、对称轴、最值、增减性、与坐标轴的交点等性质，最后师生归纳小结.

问题3：若抛物线的图象上有三点[-2，y1，] [1，y2，][4，y3，] 则[y1，y2，y3]的大小关系为      .

问题4：抛物线变换.

（1）将抛物线[y=x2-4x-5]向右平移2个单位长度，再向下平移3个单位长度后，得到的抛物线的函数表达式是      ;

（2）将抛物线先向右平移2个单位长度，再向下平移3个单位长度后得到抛物线[y=x2-4x-5，] 则原抛物线的函数表达式是      ;

（3）将抛物线[y=x2-4x-5]绕顶点旋转[180°]后，得到的抛物线的函数表达式是      ;

（4）将抛物线[y=x2-4x-5]沿直线[y=-3]作轴对称变换后，得到的抛物线的函数表达式是      ;

（5）将抛物线[y=x2-4x-5]沿直线[x=1]作轴对称变换后，得到的抛物线的函数表达式是      .

【评析】问题3回顾了二次函数中函数值大小比较的常用方法——轴对称变换法、代入法. 问题4系统梳理了二次函数平移、旋转、轴对称的图象变换，最后提炼方法，当抛物线形状不变时，只关注抛物线顶点与开口方向的变化.

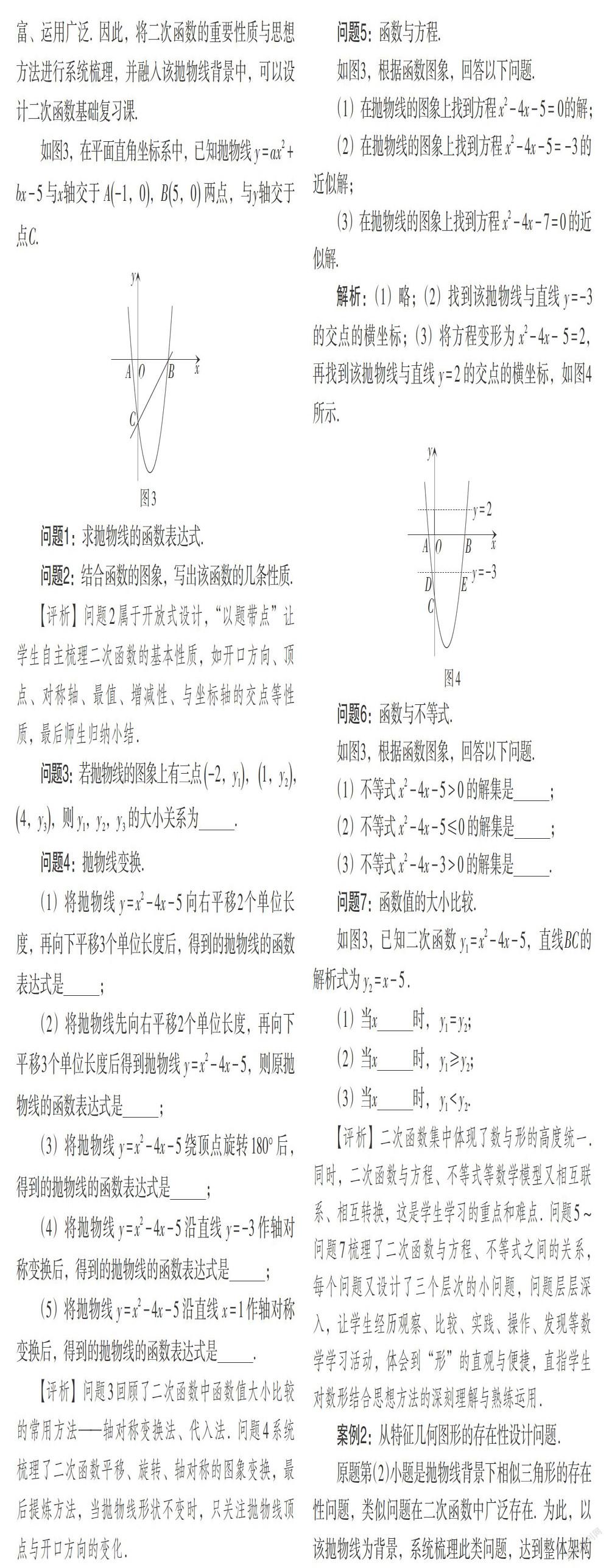
问题5：函数与方程.

如图3，根据函数图象，回答以下问题.

（1）在抛物线的图象上找到方程[x2-4x-5=][0][的解;]

（2）在抛物线的图象上找到方程[x2-4x-5=][-3]的近似解;

（3）在抛物线的图象上找到方程[x2-4x-7=0]的近似解.

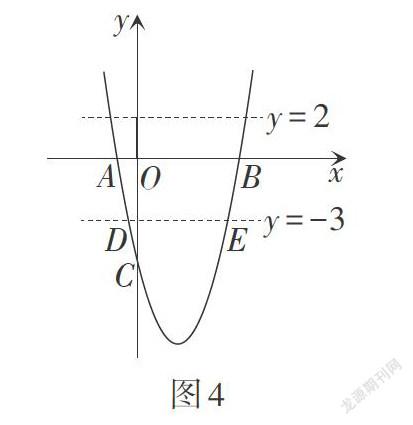
解析：（1）略;（2）找到该抛物线与直线[y=-3]的交点的横坐标;（3）将方程变形为[x2-4x-][5=2，] 再找到该抛物线与直线[y=2]的交点的横坐标，如图4所示.

问题6：函数与不等式.

如图3，根据函数图象，回答以下问题.

（1）不等式[x2-4x-5>0]的解集是      ;

（2）不等式[x2-4x-5≤0]的解集是      ;

（3）不等式[x2-4x-3>0]的解集是      .

问题7：函数值的大小比较.

如图3，已知二次函数[y1=x2-4x-5，] 直线BC的解析式为[y2=x-5].

（1）当x      时，[y1=y2;]

（2）当x      时，[y1≥y2;]

（3）当x      时，[y1<y2.]

【评析】二次函数集中体现了数与形的高度统一.同时，二次函数与方程、不等式等数学模型又相互联系、相互转换，这是学生学习的重点和难点. 问题5 ～ 问题7梳理了二次函数与方程、不等式之间的关系，每个问题又设计了三个层次的小问题，问题层层深入，让学生经历观察、比较、实践、操作、发现等数学学习活动，体会到“形”的直观与便捷，直指学生对数形结合思想方法的深刻理解与熟练运用.

案例2：从特征几何图形的存在性设计问题.

原题第（2）小题是抛物线背景下相似三角形的存在性问题，类似问题在二次函数中广泛存在. 为此，以该抛物线为背景，系统梳理此类问题，达到整体架构的目的.

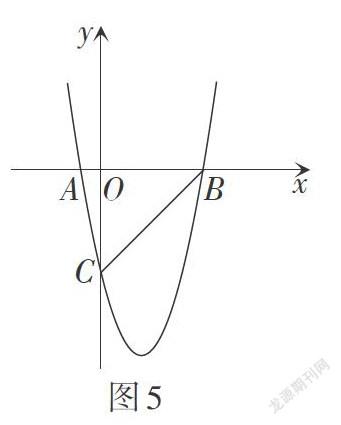
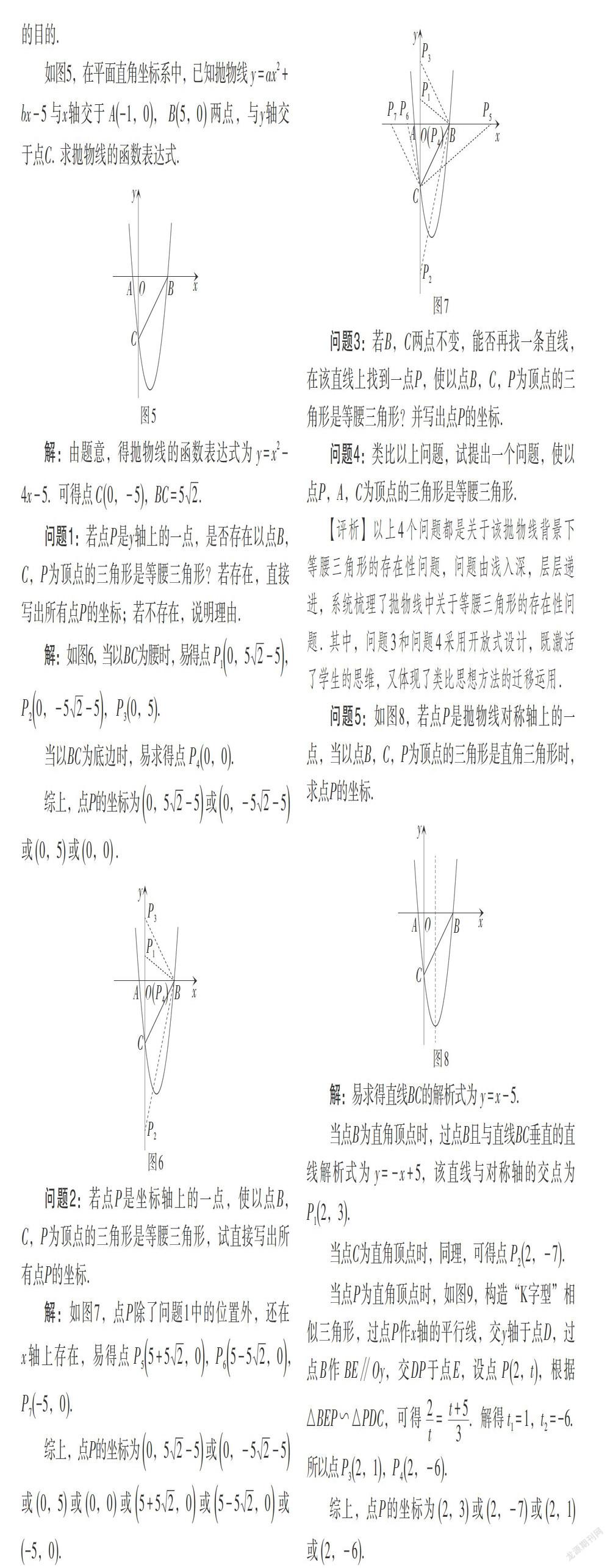
如图5，在平面直角坐标系中，已知抛物线[y=ax2+][bx-5]与x轴交于[A-1，0，] [B5，0]两点，与y轴交于点C. 求抛物线的函数表达式.

解：由题意，得抛物线的函数表达式为[y=x2-][4x-5.] 可得点[C0，-5，BC=52.]

问题1：若点P是y轴上的一点，是否存在以点B，C，P为顶点的三角形是等腰三角形？若存在，直接写出所有点P的坐标;若不存在，说明理由.

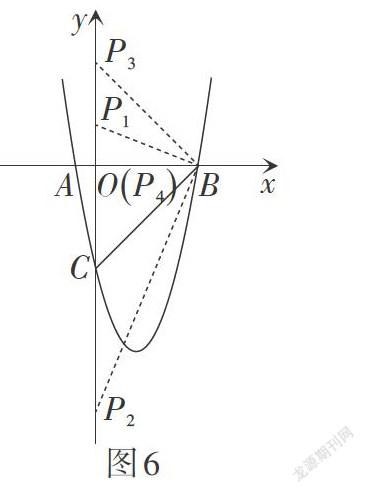
解：如图6，当以BC为腰时，易得点[P10，52-5，] [P20，-52-5，] [P30，5.]

当以BC为底边时，易求得点[P40，0.]

综上，点P的坐标为[0，52-5]或[0，-52-5]或[0，5]或[0，0].

问题2：若点P是坐标轴上的一点，使以点B，C，P为顶点的三角形是等腰三角形，试直接写出所有点P的坐标.

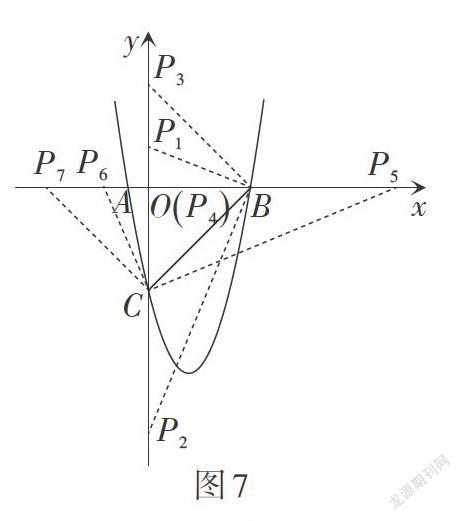
解：如图7，点P除了问题1中的位置外，还在x轴上存在，易得点[P55+52，0，P65-52，0，][P7-5，0.]

综上，点P的坐标为[0，52-5]或[0，-52-5]或[0，5]或[0，0]或[5+52，0]或[5-52，0]或[-5，0.]

問题3：若B，C两点不变，能否再找一条直线，在该直线上找到一点P，使以点B，C，P为顶点的三角形是等腰三角形？并写出点P的坐标.

问题4：类比以上问题，试提出一个问题，使以点P，A，C为顶点的三角形是等腰三角形.

【评析】以上4个问题都是关于该抛物线背景下等腰三角形的存在性问题，问题由浅入深，层层递进，系统梳理了抛物线中关于等腰三角形的存在性问题. 其中，问题3和问题4采用开放式设计，既激活了学生的思维，又体现了类比思想方法的迁移运用.

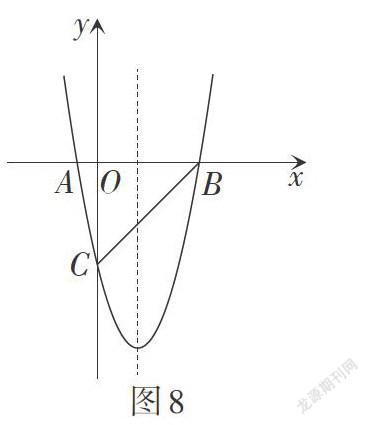
问题5：如图8，若点P是抛物线对称轴上的一点，当以点B，C，P为顶点的三角形是直角三角形时，求点P的坐标.

解：易求得直线BC的解析式为[y=x-5.]

当点B为直角顶点时，过点B且与直线BC垂直的直线解析式为[y=-x+5，] 该直线与对称轴的交点为[P12，3.]

当点C为直角顶点时，同理，可得点[P22，-7.]

当点P为直角顶点时，如图9，构造“K字型”相似三角形，过点P作x轴的平行线，交y轴于点D，过点B作[BE∥Oy，] 交DP于点E，设点[P2，t，] 根据[△BEP∽△PDC，] 可得[2t=][t+53.] 解得[t1=1，t2=-6.] 所以点[P32，1，P42，-6.]

【评析】问题5是探究抛物线背景下直角三角形存在性问题，通常采用解析法或构造相似三角形列出方程，渗透了分类讨论、方程、转化等数学思想方法. 该问题还可以进一步变式. 例如，在抛物线上找到一点P，使得B，C，P三点构成的三角形是直角三角形.

问题6：若点P在抛物线上，点Q在x轴上，当以点B，C，P，Q为顶点的四边形是平行四边形时，求点P的坐标.

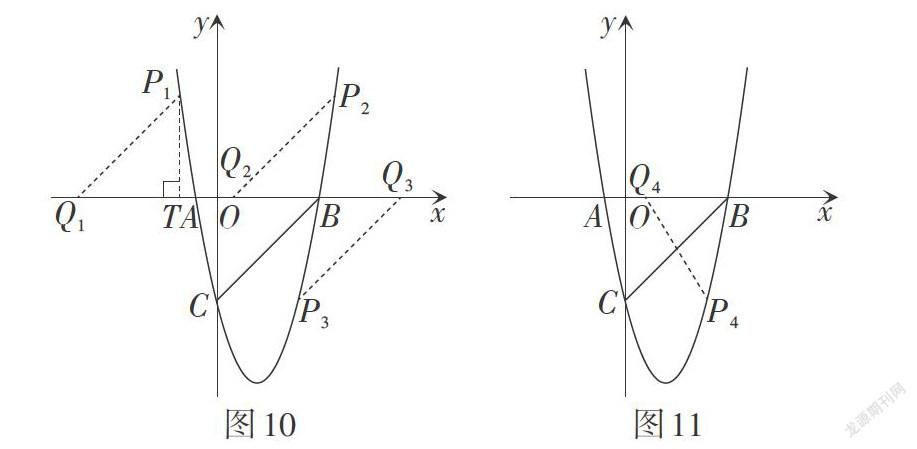
解：如图10，当以BC为边时，向左平移线段BC，分别交抛物线和x轴于点[P1，Q1，] 过点[P1]作[P1T⊥Ox]于点T，易证[△Q1TP1≌△BOC.] 易得点[P1]的纵坐标为5. 所以点[P12-14，5，] 同理，可以求出点[P22+14，5，] [P34，-5.]

如图11，当以BC为对角线时，易求得点[P4]与点[P3]重合，即[P44，-5.]

问题7：若点P在抛物线上，点Q在抛物线的对称轴上，当以点B，C，P，Q为顶点的四边形是平行四边形时，求点P的坐标.

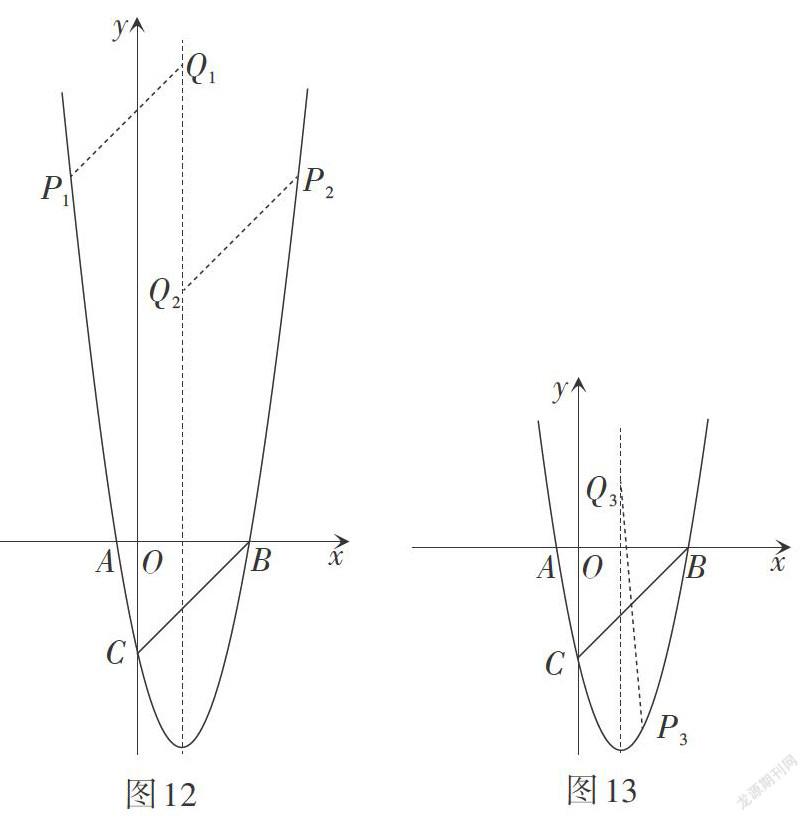
解：如图12，当以BC为边时，易求得点[P1-3，16，] [P27，16.]

如图13，当以BC为对角线时，易求得点[P33，-8.]

综上，点P的坐标为[-3，16]或[7，16]或[3，-8.]

【评析】问题6和问题7是在该抛物线背景中，系统罗列了平行四边形存在性的常见类型. 其解法是运用图形性质，将平行四边形问题转化为全等直角三角形，建立方程求解，渗透数形结合、化归、方程等思想方法.

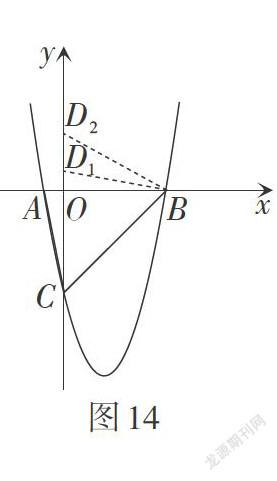
问题8：若点D是y轴上的一点，且以B，C，D为顶点的三角形与[△ABC]相似，求点D的坐标.

解：如图14，根据[∠OBC=∠OCB=45°，] 分两种情况讨论.

当[△ABC∽△DCB]时，得[ABDC=CBBC.] 因为[CD=AB=6，] 易求得点[D10，1.]

当[△ABC∽△BCD]时，得[ABBC=CBDC，] 即[652=52CD.] 所以[CD=253.] 所以点[D20， 103.]

综上，点D的坐标为[0，1]或[0， 103.]

【评析】通过设计问题1 ～ 问题8，依托同一问题背景，将平时学习中割裂的、零散的有关抛物线背景中特征几何图形的存在性问题进行有效链接、系统梳理、整体架构，促进学生结构化学习，达到由此及彼、融会贯通的目的.

案例3：利用图形面积设计问題.

原题第（3）小题考查的是动态四边形面积，动态的数学问题往往是学生学习的难点之一. 我们从静态到动态、特殊到一般、三角形到四边的设计思路出发，为学生的思维与推理搭建“脚手架”，促进学生高认知水平和能力的发展.

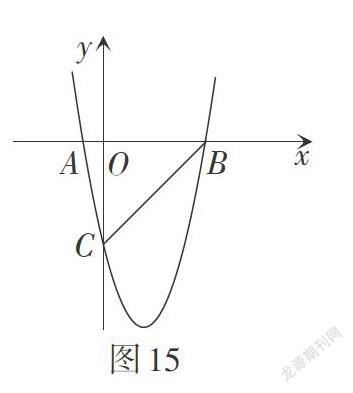
如图15，在平面直角坐标系中，已知抛物线[y=ax2+bx-][5]与x轴交于[A-1，0，B5，0]两点，与y轴交于点C.

问题1：求[△ABC]的面积.

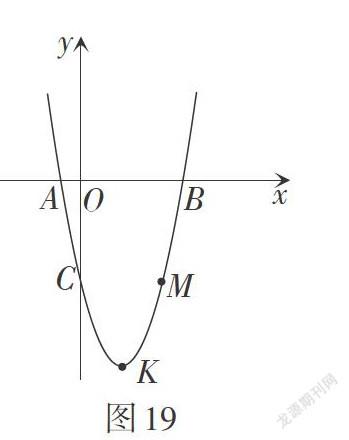
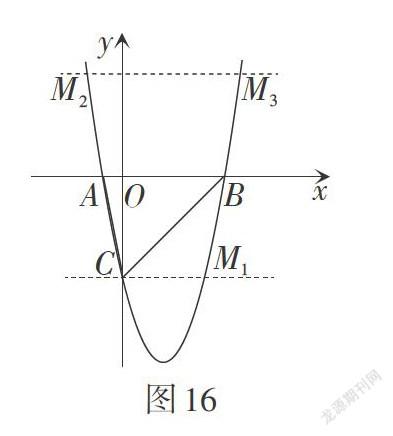
问题2：点M在抛物线上，求满足条件[S△ABC=S△ABM]的点M的坐标（点M异于点C）.

解：如图16，运用三角形等积变换，同底等高的三角形面积相等，易求得[M14，-5，M22-14，5，][M32+14，5.]

【评析】问题1和问题2均为静态三角形的面积问题，以低起点的问题调动学生学习的积极性，为后续探究打好基础.

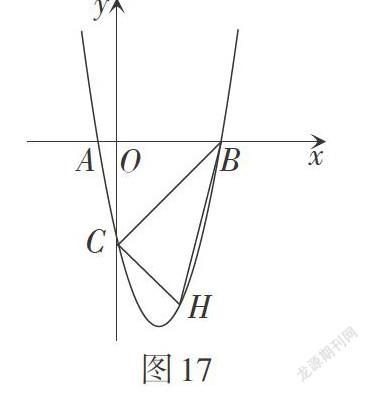
问题3：如图17，若点H是直线BC下方抛物线上的一动点，设点H的横坐标为t，连接BH，CH.

（1）求[△BCH]的面积;

（2）当[△BCH]的面积最大时，求点H的坐标;

（3）若[S△BCH∶S△ABC=2∶3]，求点H的坐标.

解：（1）求[△BCH]的面积，可采用分割法.

方法1：水平分割，过点C作x轴的平行线，将[△BCH]分割为两个水平放置的三角形.

方法2：竖直分割，过点H作y轴的平行线，将[△BCH]分割为两个竖直放置的三角形. 容易求得[S△BCH=][-52t2+252t 0<t<5.]

（2）略;（3）略.

【评析】该题是关于“一个动点”的动态三角形面积，相比问题1，思维含量明显提升. 问题3第（1）小题求[△BCH]的面积是关键，可以采用多种方法，而分割法尤其重要. 教师需讲清怎样分割，为什么要这样分割，既渗透化归思想方法（将问题3转化为问题1的形式），又顺势推出求斜三角形的面积公式，即[S=12×水平宽×铅直高.]

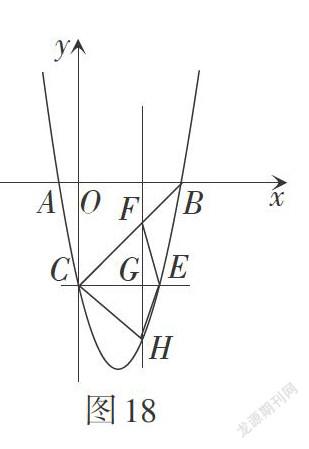
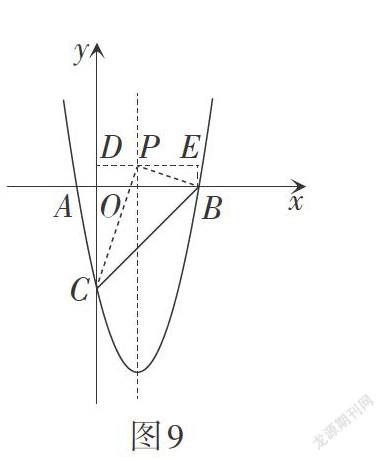
问题4：如图18，[CE∥Ox]与抛物线相交于点E，点H是直线CE下方抛物线上的动点，设点H的横坐标为t，过点H且与y轴平行的直线与BC，CE分别交于点F，G，如何求四边形CHEF的面积？你有几种求法？

解：求四边形面积有以下3种方法.

方法1：水平分割，将四边形的面积转化为[△CEF]与[△CEH]的面积之和. 由已知可得点[Ht，t2-4t-5，] [CE=4，] 直线BC的解析式为[y=x-5]，则点[Ft，t-5.] 易求得[S四边形CHEF=][-2t-522+252.]

方法2：竖直分割，将四边形面积转化为[△FHC]与[△FHE]的面积之和. 过程略.

方法3：利用对角线互相垂直四边形的面积公式[S四边形CHEF=12CE ⋅ HF]求解. 过程略.

问题5：当四边形CHEF的面积最大时，求点H的坐标及最大面积.

解：当[t=52]时，四边形CHEF的面积最大，最大值为[252.] 此时点[H52，-354.]

【评析】问题4是求由“两个动点”构成的动态四边形面积，问题更加复杂. 但在问题3解法的正向迁移下，学生不难想到采用水平或竖直分割的方法（此处分割线已存在），可将四边形面积转化为两个三角形面积之和，起到化生为熟、化难为易的目的.

案例4：借助数学模型设计问题.

原题第（4）小题是根据确定的两个点，即顶点[K2，-9]和点[M4，-5]，在坐标轴上分别找两个动点P，Q，求四边形PQKM周长的最小值. 该问题是运用“将军饮马”模型，分别将点M，K以x轴，y轴进行轴对称变换，采用“化曲为直”的求解方法. 第（4）小题综合性强，多数学生会“望题生畏”. 为此，可以以“将军饮马”模型的基础运用为切入点，从易到难、从简到繁进行设计，攻克学习难点.

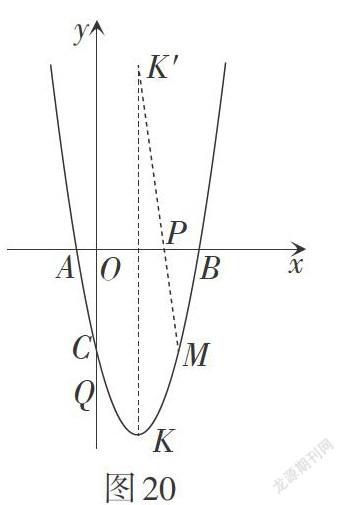
已知，如图19，在平面直角坐标系中，已知抛物线[y=x2-4x-5]的顶点为K，点[M4，m]是该抛物线上的一点.

问题1：在x轴上找一点P，使得[PK]与[PM]的和最小. 求点P的坐标.

解：如图20，作点K关于x轴的对称点[K，] 连接[KM，] 当点P为[KM]与x轴的交点时，[PK]与[PM]的和最小. 由题意，得点[K2，-9，] [M4，-5，] 通过解析法易求得点P[237，0.]

问题2：在y轴上找一点Q，使得[QK]与[QM]的和最小. 求点Q的坐标.

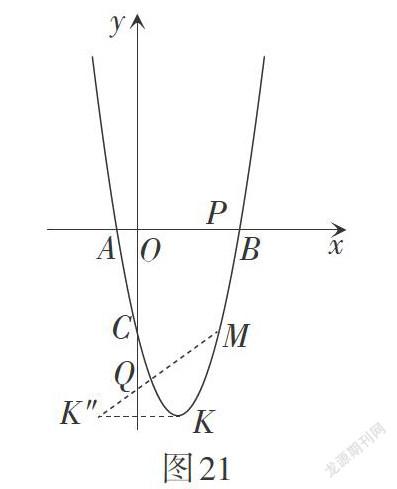
解：如图21，作点K关于y轴的对称点[K，] 连接[KM，] 当点Q为[KM]与y轴的交点时，[QK]与[QM]的和最小. 由题意，得点[K2，-9，] [M4，-5，] 通过解析法易求得点Q[0，-233.]

问题3：观察图19，你能另外再找两个点和一条直线（水平或竖直），设计一个类似问题吗？

【评析】将模型的基础运用作为设计起点，符合初中生的心理特征与认知规律. 问题1和问题2既有在水平线上找点，也有在竖直线上找点，是该模型在抛物线背景中运用的常见类型. 问题3运用开放式设计，让学生自己提出问题、解决问题. 实践表明，学生思维活跃，探究欲强，方法灵活多样. 例如，“K，M两点”不变，“线”改变，或“两点”改变，“线”不变，或“点”与“线”同时改变. 通过以上三个问题的解决，学生熟练掌握该模型在坐标平面内的基础运用，为后续学习做铺垫.

问题4：在x轴上找一点P，使得[△PMK]的周长最小. 求点P的坐标.

【评析】[△PMK]的周长等于[PM+PK+KM.] 因为KM长为定值，所以[△PMK]的周长最小时就是[PM+PK]的值最小. 这就自然转化到问题1，体现了化归数学思想方法.

问题5：在x轴和y軸上，分别找点P，Q，使四边形PQKM的周长最小，求出点P，Q的坐标.

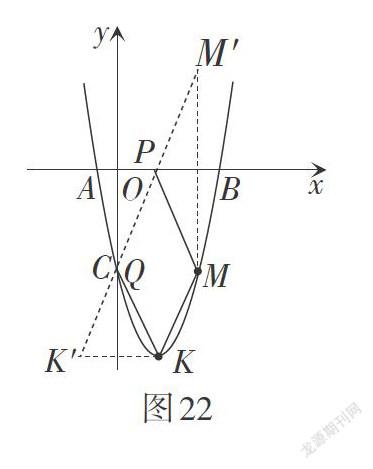
解：如图22，先利用轴对称变换找到点P，Q的位置，再分别求出点P，Q的坐标，点[P137，0，] 点[Q0，-133.]

该问题有一个疑惑，若“作点K关于x轴、点M关于y轴的对称点”，这样可以吗？这需要给学生解释不可以的理由.

问题6：你还能提出一个类似的求四边形周长最小值的问题吗？

【评析】以三角形周长最小值为铺垫，再求四边形周长的最小值，为学生铺设台阶，拾级而上，有助于学生自主探究，掌握方法，攻克难点. 问题6采用开放式设计，既突出学生的主体地位，让学生自己提出问题、解决问题，也顺势迁移，达到及时巩固的目的. 以上系列问题的层次逐渐提升，但万变不离其宗，都是运用轴对称变换，化曲为直，将问题解决回归到“两点之间，线段最短”的基本原理上去，给学生豁然开朗的学习愉悦感，有助于学生消除畏难情绪，树立学习信心.

三、思考

1. 题干是设计“一课一题”的“根”

有教师曾问，“一课一题”与通常的变式教学有什么区别？“一课一题”设计思路是什么？笔者浅见，认为“一题”即指问题的题干不变，依托同一个问题背景或情境，从某些重要的知识、方法或模型运用等为切入点，将平时学习中割裂的、碎片化的知识有效连接起来，系统架构，整体设计“一课”，使学生由此及彼，达到知识与方法的融会贯通. 显然，问题题干是设计“一课一题”的“根”，“一课一题”的设计具有更强的针对性，是具有更高要求的专题变式教学设计. 例如，本文四个案例均以抛物线[y=x2-4x-5]为“根”，以原题为切入点，将二次函数的基本性质及数形结合思想方法，特征几何图形的存在性，三角形、四边形的面积计算，“将军饮马”模型运用等融入同一个抛物线背景中，对知识与方法进行系统整合，给人以变式自如、结构紧凑、浑然一体之美感，彰显“一课一题”的魅力.

2. 系统架构是“一课一题”的“径”

如果在教学设计中能够强调系统地、整体地、联系地看待问题，把握好整体性，那么教师在教学中就能够对内容的系统结构了如指掌，心中有一张“网络图”，从而把握教学的方向，使教学有的放矢. 也只有这样，才能使学生学到结构化的、联系紧密的、迁移能力强的知识. 例如，案例2中关于二次函数中特征几何图形的存在性问题，在二次函数的学习过程中反复出现，在教学设计时，教师可以细细梳理，并做如下思考：主要有哪几类常见图形？它们以何种方式存在？解决问题的思想方法是什么？这样系统地思考，我们就有了“一课一题”设计的路“径”，可以围绕题干，采用横向拓展、纵向延伸的策略，系统架构，整体呈现，指向学生的深度学习，提升学生的数学学科核心素养.

3. 揭示本质是“一课一题”的“魂”

授人以鱼，不如授人以渔.“一课一题”的设计其实质就是通过这一课的学习，要让学生探究出一类问题的本质规律，掌握解题的本质方法，实现思想方法的归一，让数学学科核心素养落地. 为此，在教学环节或者课堂小结中，教师要适时让学生自主提炼（或师生共同提炼），并感悟解决问题的思想方法，这样学生才能举一反三、迁移运用、融会贯通. 例如，案例2中几何图形的存在性，渗透了分类讨论思想，为此，就需要学生提炼并感悟到：分几类？如何分类？为什么要这样分类？同时，在直角三角形和平行四边形的存在性问题中，还需要揭示出“如何将图形化归到相似（全等）直角三角形，并建立方程”，深刻领悟化归、方程等数学思想方法. 案例4中关于“将军饮马”模型的运用，虽然问题多变，但万变不离其宗，其本质都是运用轴对称变换“化曲为直”，将问题解决回归到“两点之间，线段最短”的基本原理. 史宁中教授曾说：数学学科核心素养是数学思想方法的具体体现. 加强学生数学学科核心素养的培养，就需要我们在解题过后，适时提炼数学思想方法，这就是“一课一题”的“魂”之所在.

“一课一题”具有切口小、内容精、方法准的特点，广受师生喜爱，是一种行之有效的小专题复习课类型. 加强“一课一题”的教学设计与研究，既能使学生将所学知识关联化、体系化，促进知识方法的联通与融合，也有助于教师更好地把握教材体系，提升教师的教学设计能力，促进教师的专业成长.

参考文献：

[1]章建跃. 从整体性上把握好数学内容[J]. 中小学数学（高中版），2010（3）：封底.