王 博 宋义壮

( 山东师范大学数学与统计学院,250358,济南 )

1 引 言

MRI和CT等成像模式总是受到各种伪影的影响，比如MRI中的运动伪影、CT中的金属伪影和射线束硬化等[1]. 此外，各种随机因素的干扰会使成像中含有噪声. 这些伪影和噪声的存在降低了成像质量而导致图像达不到临床应用对高分辨率医学图像的需求. 对受到伪影和噪声影响的医学图像进行图像恢复是实现高分辨率医学成像的一种方法. 本文考虑伪影造成图像模糊且噪声为高斯白噪声的特殊情形，针对这一特殊情形给出降噪和去模糊的数学算法，并对算法的可行性进行理论和数值验证.

记u0∈n×n为由医学成像设备所得到大小为n×n含有噪声的模糊图像，A∈m×m表示尺寸为m×m的模糊核，η∈n×n为随机高斯噪声，则A以及η之间满足如下线性关系：

u0=A*u+η.

(1)

其中*表示卷积.本文旨在由(1)式恢复高分辨图像u∈n×n. 注意到利用人体某些部位的MRI、CT图像的稀疏性，本文拟采用如下稀疏优化模型：

(2)

上式右端第一项为保真项，第二项为正则化项，λ>0为权衡两项的参数.Dv=(D(1)v;D(2)v)∈2n×n表示v的离散梯度，其中D(1)v,D(2)v∈n×n分别为水平方向与垂直方向具有边界条件的一阶离散偏导. 当q=0时，模型(2)为精确模型;当l0最小化,为著名的N-P难问题[2]. 文献[3]提出了经典的总变差降噪模型，陶哲轩和Candes利用压缩感知(即q=1)的方法实现了稀疏正则化，但l1正则化在图像细节上的恢复效果还需进一步提升. 文献[4]发现超拉普拉斯分布更符合自然图像的梯度分布，由此提出了lq(q∈[0.5,0.8])正则化模型.

注意到问题(2)的非凸性，为求解(2)式的lq(q∈[0.5,1])稀疏优化模型，文献[5]提出半二次最小化方法：其基本想法是引入辅助变量w=(w(1);w(2))∈2n×n，并通过二次惩罚项使辅助变量w逼近梯度Dv,w(1),w(2)∈n×n. 由此得出(2)式的lq(q= 1,1/2,2/3)近似优化模型：

(3)

其中α为二次惩罚参数. 当α→时，(3)式的解收敛于(2)式的解. 文献[4,6]利用交替迭代的半二次算法求解(3)式. 为提高算法的有效性，文献[4]对参数α进行递增迭代.即设第k步迭代参数α的值为αk=α1·(αloc)k-1,其中初值α1>0，实数αloc>1.lq(q= 1,1/2,2/3)半二次分裂算法可表示为

(4)

(5)

这里的wk与uk分别表示(4)式与(5)式迭代第k步的解. 为方便介绍，在下文称(4)式为w子问题，(5)式为u子问题. 由于相关文献均未涉及半二次分裂算法的收敛性分析，本文旨在对算法的收敛性分析进行讨论，并通过实验结果得出医学图像梯度的稀疏性与各正则化算法选取的关系. 为叙述方便起见，下面将首先给出半二次算法的一个简要回顾.

2 半二次算法回顾

对于w子问题(4)(q=1,1/2,2/3)，文献[6,7]给出了求解该问题的解析表达式. 设[ · ]i,j,i,j=1,…,n表示矩阵的第(i,j)个分量，那么w子问题(4)可分解为2n2个一维最小化问题：

(6)

这里的l=1,2，v∈. 定义(6)式的解算子为

(7)

下面分别给出当q= 1,1/2,2/3时，算子(7)的解析表达式.

1) 当q=1时，可利用经典的软阈值公式求解：即∀x∈，

(8)

2) 当q=1/2时，可利用硬阈值公式[5]求解：即∀x∈，令则

(9)

3) 当q=2/3时，可利用闭阈值公式[6]求解；即∀x∈，令

则

(10)

定义w子问题的解算子为

(11)

通过(8)-(10)式及算子(11)可知，lq(q= 1,1/2,2/3)半二次算法w子问题第k步迭代的解可表示为

[wk]i,j=Sαk,q([Duk-1]i,j)=(hαk,q([D(1)uk-1]i,j);hαk,q([D(2)uk-1]i,j)) ,i,j=1,…,n.

(12)

对于u子问题(5)，设N=n2，矩阵D(1),D(2),A∈N×N分别为算子D(1),D(2),A的矩阵形式，N分别为的列向量形式,则(5)式的欧拉-拉格朗日方程表示为

(13)

文献[4]提出了求解(13)式的快速算法，若边界条件为周期边界条件，由周期边界条件与模糊核定义可知ATA，(D(1))TD(1)，(D(2))TD(2)均为块循环阵，因此(13)式可转化为相应的卷积形式. 利用二维离散傅里叶变换与卷积定理，得lq(q= 1,1/2,2/3)半二次算法u子问题第k步迭代的解为

(14)

其中F(·)表示快速傅里叶变换，IF(·)表示傅里叶逆变换，F(·)*为F(·)的复共轭，°表示分量乘法，除法为分量除法. 由于D(1),D(2),A的快速傅里叶变换可以预先计算，因此上式每次迭代只需进行两次傅里叶变换和一次傅里叶逆变换. 下面将在第3部分给出半二次算法的一个收敛性分析.

3 收敛性分析

本部分主要对lq(q= 1,1/2,2/3)半二次算法收敛性进行讨论.u子问题快速算法与算法的收敛性分析难以同时保障，我们将通过医学图像的先验信息解决此问题. 由于医学图像u边界点的像素值恒为0，在此基础上可得出下列半二次算法的收敛性定理.

定理1序列{(uk,wk)}由lq(q= 1,1/2,2/3)半二次算法给定，那么当k→时，{(uk,wk)}收敛.

证由半二次算法定义可知，系数α1>0且αloc>1. 因此当k→时，αk=α1·(αloc)k-1→. 下面证明当k→时，w子问题(q=1,1/2,2/3)的解算子Sαk,q为恒等算子.

1) 若q=1. 代入(8)式可知，当αk→时，阈值则当x≠0时，有hαk,1(x)→x. 又因为hα,1(0)=0，因此∀x∈

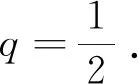
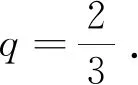
由上述结论可知，当k→时

[wk]i,j=Sαk,q([Duk-1]i,j)

=(hαk,q([D(1)uk-1]i,j);hαk,q([D(2)uk-1]i,j))

= ([D(1)uk-1]i,j;[D(2)uk-1]i,j)

=[Duk-1]i,j,i,j=1,…,n.

(15)

对于u子问题，设wk=(wk(1);wk(2))∈2N为wk的列向量形式，矩阵D=(D(1),D(2))∈2N×N，则(13)式可表示为

通过上式可知，当αk→时，DTDuk=DTwk. 由(15)式可知wk=Duk-1，因此DTDuk=DTwk=DTDuk-1. 在周期边界条件下D(1),D(2)为奇异矩阵，此时DTD为非满秩矩阵，为实现u子问题快速算法的同时保证D(1),D(2)为满秩矩阵. 可令u在边界条件下对应的离散梯度为

由于医学图像边界点的像素值恒为0，此时该离散梯度与周期边界条件对应的离散梯度相同，由于在该条件下矩阵D为列满秩矩阵，因此可知DTD∈N×N为满秩矩阵. 当k→时，uk=(DTD)-1DTDuk-1=uk-1,再由(15)式可知wk=wk-1. 从而得出结论，当k→时，序列{(uk,wk)}收敛.

下面将在第4部分给出该算法的数值仿真实验.

4 数值仿真

为验证算法的有效性，本部分将通过几组实验比较l1、l1/2与l2/3稀疏优化模型通过半二次分裂算法对医学图像的恢复情况，实验参数α1=1，αloc=4，迭代次数T=15. 图像质量通过信噪比[5](PSNR)衡量，定义如下

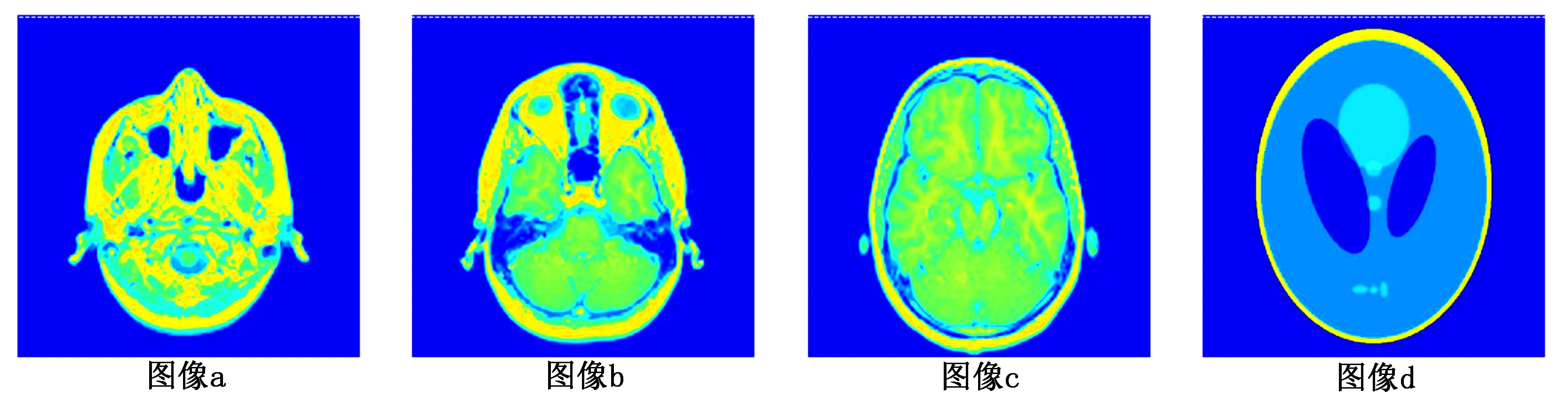
图1 测试图像

算法有效性将从图像恢复质量(PSNR)与算法迭代速度(迭代时间)两个方面衡量. 表1展示了退化图像(含有噪声的模糊图像)u0与l1、l1/2、l2/3正则化方法恢复图像的PSNR值，后三栏展示了l1、l1/2、l2/3正则化方法迭代所需时间. 通过实验数据可知，在迭代速度方面，l1与l1/2正则化方法恢复速度具有明显优势. 在图像质量方面，根据表1可知，测试图像a、b、c运用l1正则化方法恢复图像的PSNR值高于其它方法. 对于测试图像d，则是l1/2正则化方法更有优势. 出现这一现象可能与图像的梯度分布有关，为验证这一猜想， 定义图像的稀疏比为

表1 不同正则化方法下恢复图像的PSNR值以及算法的迭代时间

SR(u)≜Z(u)/P(u),

其中u为清晰图像，Z(u)为u梯度模的零项个数，P(u)为图像像素个数.通过上述定义可知稀疏比可以衡量图像梯度分布的稀疏程度，稀疏比越高则图像梯度越稀疏. 各正则化方法的相对恢复效果则由恢复图像PSNR值的离差(即真实值与平均值的差值)衡量，离差越大则说明恢复效果相对更好. 表2给出了各稀疏正则化方法恢复图像的离差与相应清晰图像稀疏比之间的对应关系，并通过图2展示该稀疏比与离差的变化关系. 根据表2及图2可知，清晰图像的稀疏比与l1/2正则化恢复图像离差的数值关系成正相关；随着清晰图像稀疏性增强，恢复图像离差由负值递增为正值，由此可知清晰图像的稀疏比越高，l1/2正则化方法的相对恢复效果越好. 对于l1正则化方法，清晰图像稀疏比与恢复图像离差的数值关系成负相关，因此l1正则化方法更适合对梯度分布非稀疏的图像进行恢复. 对于l2/3正则化方法，其恢复图像的离差值稳定且近似为0，说明l2/3正则化方法恢复图像的PSNR值与各正则化方法恢复图像的PSNR值均值一致，因此l2/3正则化方法的图像恢复效果更稳定. 在已知图像先验信息的前提下，对于梯度分布稀疏的图像可以选择l1/2正则化算法进行恢复，反之则选择l1正则化算法. 对于图像梯度分布未知的图像，可选取l2/3正则化算法进行恢复.

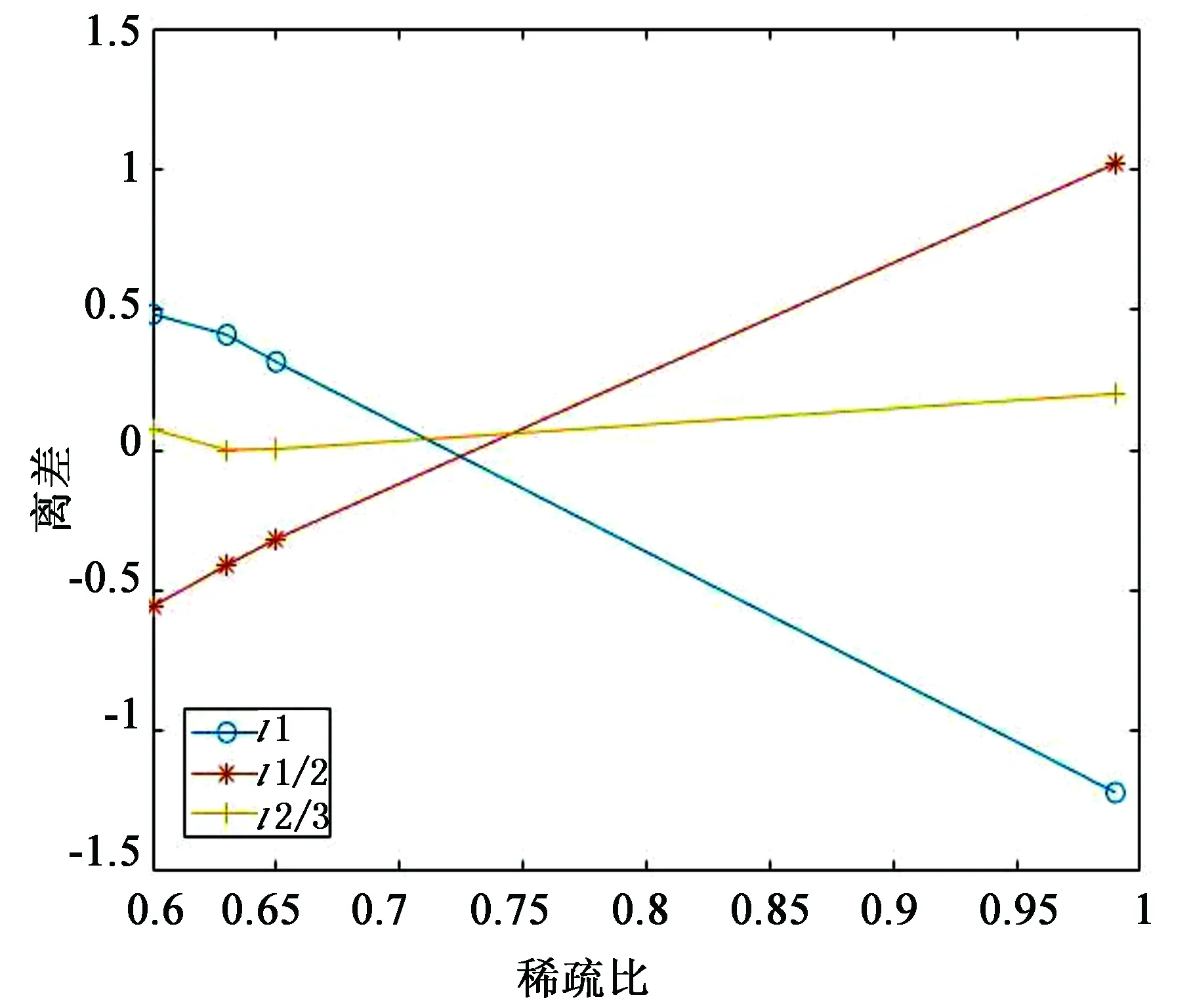
图2 稀疏比与各正则化离差对比图

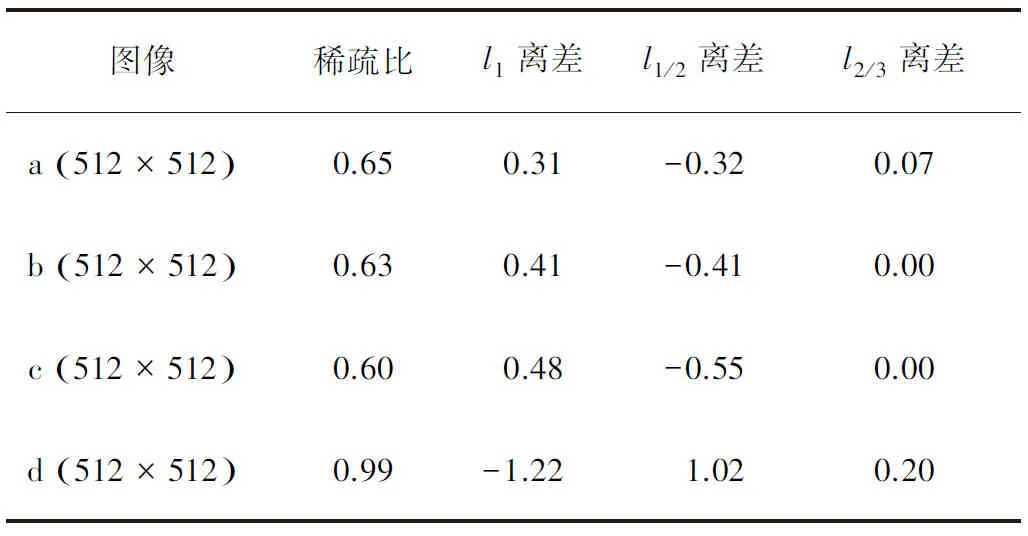
表2 各图像的稀疏比与不同正则化方法的离差值

由于篇幅有限，图3仅展示了图像a与图像d在不同正则化方法下的恢复图像的对比图. 为更直观地比较图像细节的恢复效果，图3最后一栏展示了图像d的部分区域. 为凸显图像恢复细节的对比效果，本文对局部区域恢复结果进行了放大与对比度增强处理. 通过图3可以看出，运用l1/2与l2/3正则化方法对稀疏图像d进行恢复，其细节恢复效果基本一致.l1正则化算法则无法有效兼顾降噪与去模糊的效果.

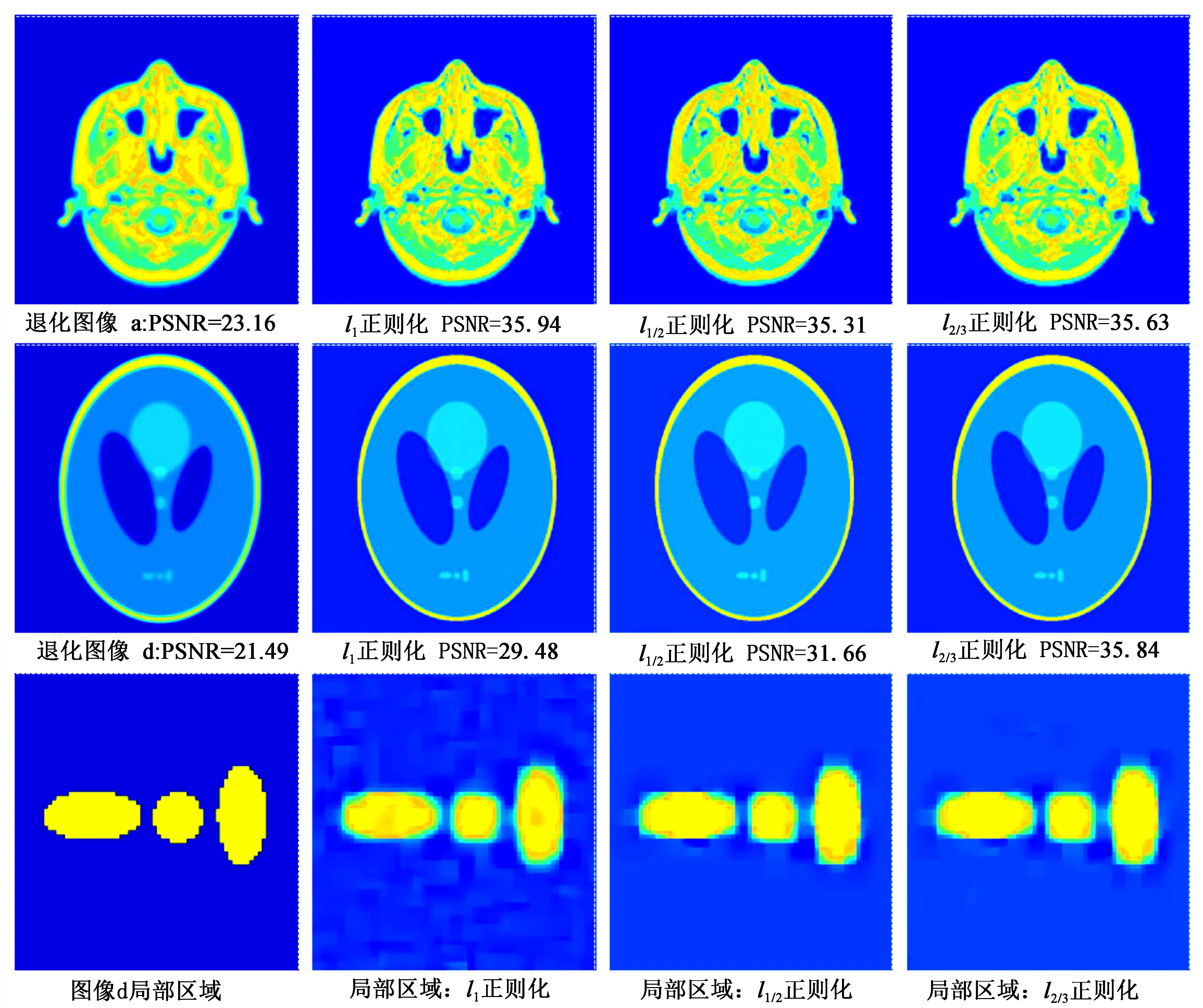
图3 恢复图像对比图

通过实验可得出下列结论.从算法速度考虑，l1与l1/2正则化算法在速度上更有优势. 从算法质量考虑，对于身体不同部位的MRI和CT图像，可以通过医学图像的先验信息给出不同图像的梯度分布，由图像的梯度分布选择恰当的稀疏优化模型对图像进行恢复.l1/2正则化算法在迭代速度具有优势的基础上，针对梯度分布稀疏的医学图像，具有良好的降噪与去模糊效果.

5 总结与展望

本文基于稀疏优化模型实现医学图像的降噪与去模糊，并利用半二次算法对模型进行求解. 为解决非凸优化问题半二次算法的收敛性问题，通过医学图像的先验信息给出了非凸情况下半二次算法的一个收敛性定理. 数值实验部分，本文针对梯度分布不同的四组医学图像，分别运用l1、l1/2、l2/3正则化的半二次算法对医学图像进行降噪与去模糊处理，并通过实验结果得出各正则化算法的恢复效果与医学图像梯度分布的关系. 对于梯度分布稀疏的医学图像，本文建议利用l1/2正则化方法对图像进行恢复，针对梯度分布稀疏图像的细节部分，l1/2正则化方法可以在图像去模糊的同时有效进行降噪，在迭代速度上该方法也具有一定优势.

本文工作依然存在一些局限性，虽然给出了非凸情况下半二次算法的收敛性定理，但算法的数值解是否收敛到真解还需进一步研究. 如何给出图像梯度分布与算法恢复效果相关性的严格证明，是下一步工作中的重点. 近几年分数阶导数在不同领域上具有很多进展[8]，能否把分数阶导数引入到非凸稀疏优化模型中对医学图像进行恢复，这将是一个新的研究课题.