胡星宇, 肖经渊, 李东行

（1. 广州工商学院 基础教学部，广东 广州 510850；2. 广东金融学院 金融数学与统计学院，广东 广州 510521）

文献[1]中，在广义拓扑中引入了可数μ-强仿紧空间，可数μ-θ加细空间，并证明如果广义拓扑空间X是可数μ-强仿紧空间，那么X满足条件(A*)：对于空间X中任意一个递增的非空μ-开子集列{Wi} ，并且满足X ，都存在X的μ-闭子集序列{Fi} , 使得对于每一个i=1,2,…，都有 Fi⊂Wi成立，并且=X. 此外，通过一个例子证明存在既是可数μ-θ加细同时又是μ-正规的空间X，但是X不满足条件 ( A*). 在此基础上，还给出了可数μ-θ加细空间，可数μ-强仿紧空间和条件(A*)之间的关系.在这里自然有一种想法，如果将可数μ-θ加细空间换成可数μ-弱仿紧空间，那么他们之间的关系是否仍然成立呢？在这里将详细讨论.

1 预备知识

首先给出一些基本概念和符号.

定义1[2]设X是一非空集合，如果X的子集构成的集族μ满足下面2个条件：

（2）μ的任意多个元素的并属于μ，

那么，μ称为X上的广义拓扑，(X,)μ称为广义拓扑空间.

令β⊂exp(X)和 Ø ∈β，如果 μ ={∪β':β'⊂ β}，那么β被称作μ的基，也可以说μ是通过β生成的. 如果Х∈β，那么广义拓扑空间(X,μ)被称作μ-空间.

如果X的子集B∈μ(ХВ∈μ)，则В被称作μ-开集（μ-闭集），μc表示X的全体μ-闭集构成的集族.所有包含点x∈X的μ-开集都将用μx表示，即μx= { U ∈μ:x∈U}.（△代表指标集）

定义2[3](1) 则如果对任意x, y∈X 并且x≠ y，都存在和 Uy∈μy，使 y ∉Ux和 x ∉ Uy.

(2) 则如果对任意x, y∈ X 并且x≠ y，都存在和 Uy∈μy，使.

(3) 则如果对任意x∈X和X任意一个μ-闭子集，当x∉F，都存在和UF∈μ使 F ⊂UF，并且 Ux∩UF=Ø.

(4) 则如果对X的任意2个不相交的μ-闭子集F1和F2都存在U1, U2∈μ，使 F1⊂ U1和 F2⊂ U2,并且U1∩U2=Ø.

定义4[4]令X是广义拓扑空间，再令ξ和ψ是X的μ-开覆盖，如果ξ⊂ψ，那么ξ被称作是ψ的μ-子覆盖.

定义5[4]设(X,μ)是广义拓扑空间，ς是X的子集族，ς被称作是μ-局部有限的(μ-点有限的），当且仅当对于每一个x∈X，都存在，并且Ux只跟有限个ς的元素相交（x属于ς中有限个元素）.

定义6[4]设(X,)μ是广义拓扑空间，ς是X的-μ开覆盖，X的-μ开子集构成的集族ϑ被称作是ς的-μ开加细，如果ϑ是X的覆盖，并且对于每一个U∈ϑ，都存在V∈ς,有U⊂V成立.

定义7[1]广义拓扑空间(X,)μ被称作是可数μ-强仿紧空间，当且仅当对X的每一个可数μ-开覆盖都有一个星有限的-μ开加细覆盖.

定理2[5]如果X是拓扑空间，那么下面2个结论是等价的：

(1) X是正规空间.

(2) 对于X每一个点有限的开覆盖{Uα：α∈Δ} ,都存在X的开覆盖{Vα：α∈Δ} ，并且对于每一个α∈Δ，都有成立.

2 主要结果

首先在广义拓扑空间中给出可数-μ仿紧空间，可数-μ弱仿紧空间的定义.

定义8[1]广义拓扑空间(X,)μ被称作是可数-μ仿紧空间（可数-μ弱仿紧空间）当且仅当对X的每一个可数-μ开覆盖都有一个-μ局部有限（-μ点有限）的-μ开加细.

推论1[1]在一般拓扑空间中，参考文献[6]中的图6.4，有可数强仿紧空间可数仿紧空间⇒可数弱仿紧空间⇒可数θ加细空间. 在广义拓扑空间中，很显然也有可数μ-强仿紧空间⇒可数μ-仿紧空间⇒可数μ-弱仿紧空间⇒可数μ-θ加细空间成立.

定义9[5]拓扑空间X是可数仿紧空间当且仅当X满足下列条件：(A)对于空间X中任意一个递增的非空开子集列 W ⊂W ⊂…，并且满足，都存在X的闭子集序列 F ⊂F⊂…使得对于每一个i=1,2,…,1212都有 F ⊂W，并且.ii

将要证明定义9在广义拓扑空间中是不成立的.

接下来，将会用一个例子来说明存在一个-μ空间X，它是μ-T4空间而且满足下面这个条件*(A)，但是它不是可数-μ弱仿紧空间（同样也不是可数-μ仿紧空间或可数-μ强仿紧空间）：

(A*)对于μ-空间X中任意一个递增的非空μ-开子集列W ⊂W ⊂…，并且满足，都存在X12的μ-闭子集序列F⊂F⊂…使得对于每一个i=1,2,…，都有 F ⊂W，并且.12ii

例1[1]令 X = ( 0,1)是单位开区间， β ={Ø } ∪ （ { 0， a ) ,(a , 1):a ∈(0,1)}.考虑X上的μ-基β生成的广义拓扑空间μ( β)，以下结论成立：

(1)如果A是X的μ-开子集，那么A是下面其中一种集合：

(2)如果B是X的-μ闭子集，那么B是下面其中一种集合：

(e)[r, s]; r, s ∈ ( 0,1)和r≤s（在这里假设[a, a]={a}）.

结论1[1]( X ,μ( β) )是μT2空间.

结论2[1]( X ,μ( β) )是μT4空间.

结论3[1]如果 W1⊂W2⊂…是X非空递增的μ-开子集序列，那么集合 W1, W2，…不可能有如下形式：(0,r) ∪ ( s, 1 ),r, s ∈ ( 0,1)且r≤s.

结论4[1]X满足条件 ( A*).

结论5[1]X拥有一个μ-可数基.

现在将会证明X不是可数μ-弱仿紧空间（可数μ-强仿紧空间）. 考虑X的可数μ-开覆盖并且，C满足如下结论：

结论6C没有点有限的μ-开加细覆盖.

证明 用反证法. 假设X存在点有限的μ-开加细覆盖，令C*={Uα：α∈Δ}是C的一个点有限的μ-开加细覆盖，因为 C*是C的μ-加细，所以对于每一个α∈Δ，一定存在aα∈ ( 0,1)，使得 Uα= ( 0,aα).因为 C*覆盖 X = ( 0,1)，并且sup{aα:α ∈Δ} =1. 所以，对于每一个x∈(0,1)，x都被 C*覆盖了无限多次，从而产生了矛盾，因此， C*不是点有限的μ-开加细覆盖.

结合推论1，通过以上讨论有如下定理：

定理 3存在满足条件 ( A*)的 μ -T4空间X，X不是可数μ-弱仿紧空间（同样也不是可数μ-仿紧空间或可数μ-强仿紧空间）.

接下来将会研究可数μ-强仿紧空间、可数μ-弱仿紧空间和满足条件(A*)的μ-正规空间之间的关系.

仿照在一般拓扑空间中Engelking关于可数仿紧空间［5］定理5.2.1(i) ⇔ (ii)的证明，从而给出可数仿紧空间（可数弱仿紧空间）等价刻画的方法［5］，引理5.3.5.给出在广义拓扑空间中相似的等价刻画.

引理1[1]对于任意一个μ-空间X，下面2个条件是等价的:

(1)X是μ-正规空间.

(2)对于每一个点有限的μ-开覆盖{Uα:α ∈Δ}，都存在X的一个μ-开覆盖{Vα:α ∈Δ} ，并且对于每一个α∈Δ，都有成立.文献[1]已经证明对于每一个可数μ-强仿紧空间（不一定是μ-正规空间）满足条件 ( A*).

定理4[1]每一个可数μ-强仿紧空间都满足条件 ( A*).

定理5每一个满足μ-正规性的可数μ-弱仿紧空间X都满足条件 ( A*).

最后，得到了可数μ-强仿紧空间，可数μ-弱仿紧空间和条件(A*)之间的关系，并且通过图1来表现它们之间的关系，进一步推广了文献[1]的结论.

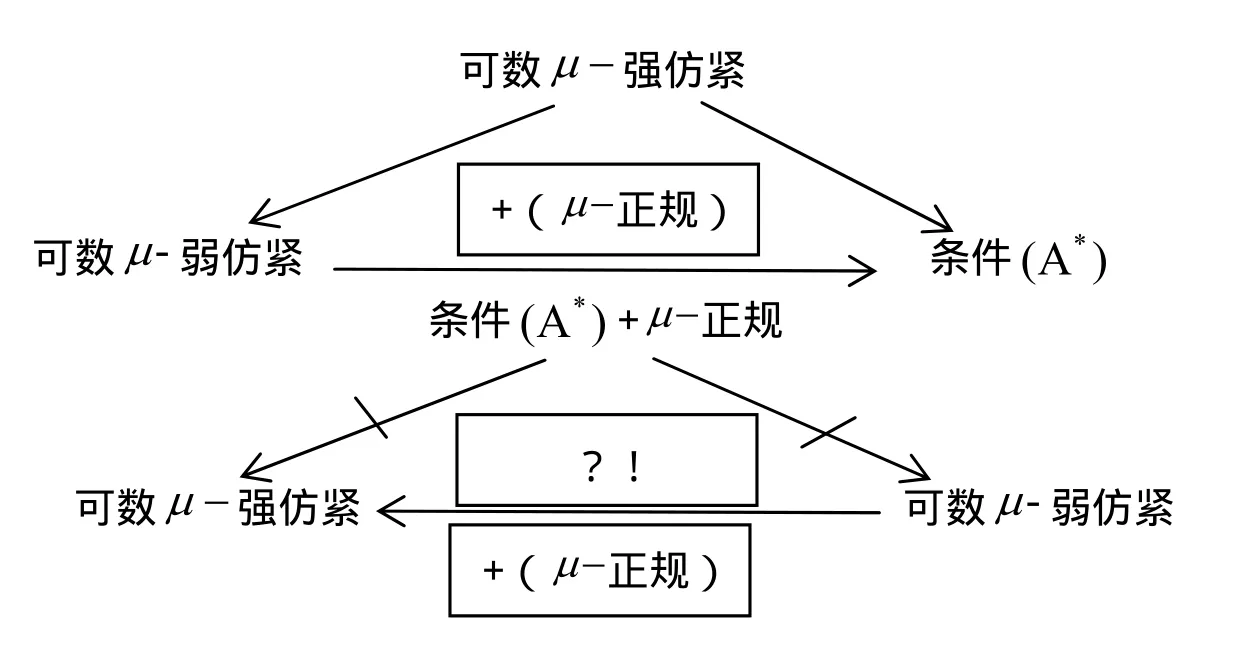
图1 可数-μ弱仿紧空间关系图