杨兆新，魏岳嵩，贾伟亚①

（淮北师范大学 数学科学学院，安徽 淮北235000）

0 引言

在线性回归模型中进行变点检测和估计是统计学中的一个常见的研究内容. 文献［1］考虑线性回归模型中变点数目问题，但在检测变点位置时需要2个阶段. 文献［2］考虑用分位数LASSO（Least absolute shrinkage and selection operator）方法对变点的数目和位置进行后验检测，但使用的方法相对笨拙. 文献［3-5］考虑LASSO估计框架内分段常数模型中的一个简单位置变点问题. 文献［6］考虑将分段常数变点问题推广为分段线性模型，并在［7-10］中给出一个更一般的线性场景. 本文利用分位数LASSO 方法研究线性回归模型变点位置估计问题，主要给出当估计的变点数和变点的真实数目一致时，变点位置估计的收敛速度.

1 模型与假设

考虑如下线性回归模型：

假设1 均值μ∗k∈R，其中k=1,2,…,K∗+1.

假设2 随机误差项有概率密度f(x)，且 |f′(x)|＜∞.

假设3其中{δn} 是递减序列，且δn→0(n→∞).

假设4 记且n→∞时，λn δn→0.

假设5 变点的数目Κ∗∈Ν 固定不变.

2 主要结论与证明

变点位置βn的分位数LASSO估计量为

证明根据文献［11］中引理3，引理得证.

引理2 设A 和B 是2个随机变量，x是任意正实数，，则对于任意常数v ＞1，有

证明由于 ||A+B ≥ ||A-||B ，故由题设知

因此

引理得证.

引理3 令是两个正的序列，满足且满足假设2. 则有

其中F是εi的分布函数.

证明首先，由概率的性质有

通过Dvoretzky-Kiefer-Wolfowitz's不等式［12］对于独立的伯努利随机变量I{}

εi≤t，当ε ＞0，

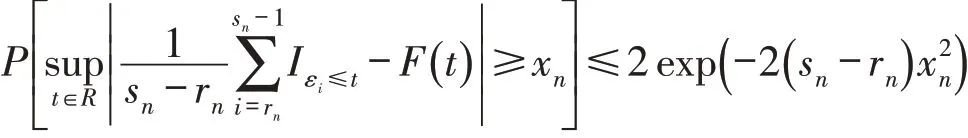
引理得证.

定理1 当，且满足假设1到假设5，有

证明根据引理1，当，当l=k时

根据引理2，当x=2nλn，不变量令随机变量A 和B 为

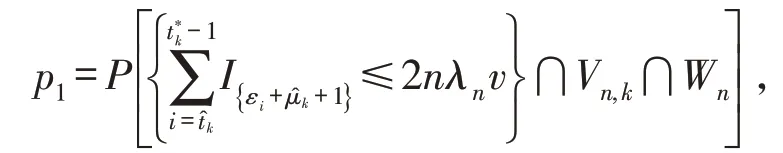
根据假设2假设4和假设5，通过引用文献［13］中的定理2，可以得到以下等式成立：

这意味着存在一个不变量c1＞0，

根据文献［14］和式（3），可以得到

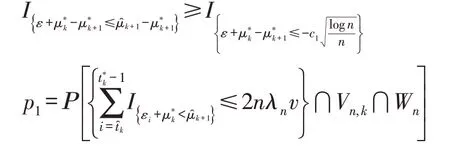
通过假设2对于所有x∈R，，存在一个不变量C ＞0，使

当n趋向于无穷大时概率收敛到1. 由假设4，可得

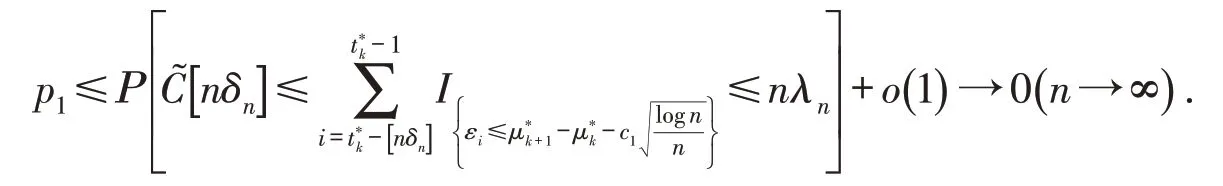
p2的证明过程与p1相似，最终可以得到

而

根据式（3）可知

且概率收敛到1，因此得

由引理3可得

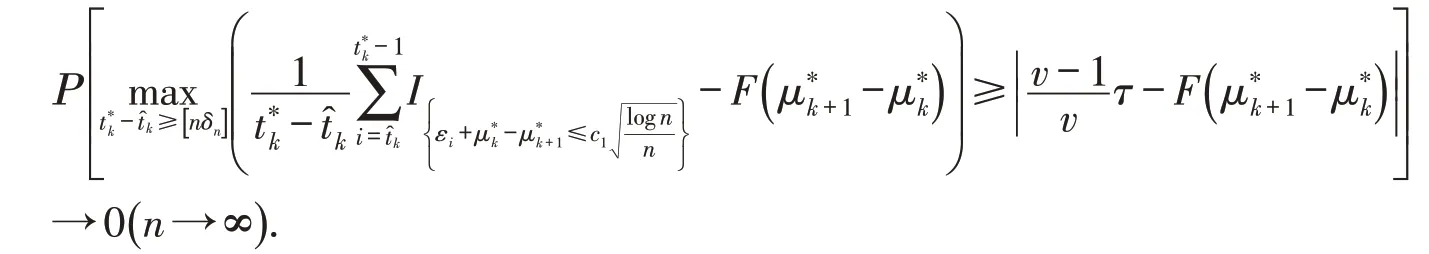
定理2 当，且满足假设1到假设5，有

证明其中，使用文献［11］中的符号

所以

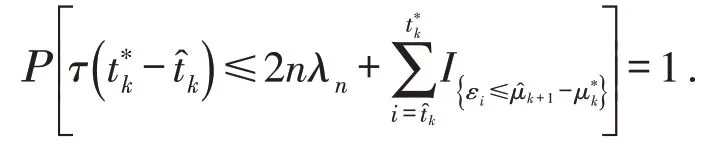
因此

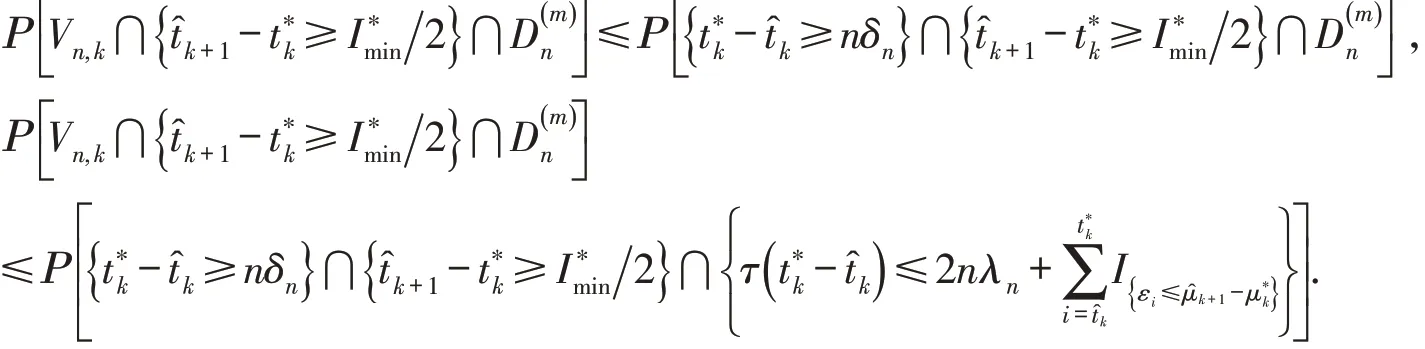
对于任意的i=k+1,k+2,…,K∗，

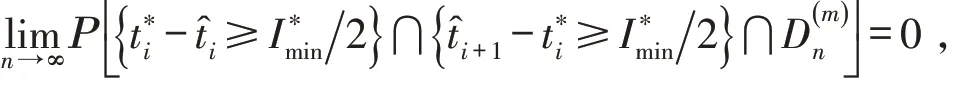
定理3 当，且满足假设1到假设5，有

证明由假设5和文献［15］，对于任意的k=1,2,…,K∗，定理可以变换为根据定理1和定理2的证明结果，定理得证.