曹振民

（中国路桥工程有限责任公司，北京 100011）

0 引言

本福特定律给出了一堆按照一定方法选取的数字中首位数字的一些分布规律，并在实际工作中得到了应用.而在数论研究中，我们有时也经常需要了解一堆有一定规律（如连续自然数）的数字中末位数字[1]或者各种数字位数的分布规律情况，如连续自然数及其乘积在数论分析、计算机浮点计算等方面就得到了一定的应用.一些学者对此进行了相关研究[2-3]，但都是针对一些特例进行，不具备全局性.总的来说，目前对连续自然数及其乘积专门研究的还不多.

今设集合X，Y 分别为：

其中，[x1，x2]表示从x1到x2的连续自然数，[y1，y2]同理.在X 和Y 之间建立一个的二元关系——一般意义上的相乘关系，设它们的乘积为S={（x，y）|x∈X，y∈Y，x*y}，显然X，Y 和S 均为有限集.本文将在对集合X，Y 及其乘积S 中的各种数字的奇偶性分析的基础上[4]，再对其位数进行分析.

所谓位数，指的是对于任意自然数x 有几位数，本文用符号Len（x）（x∈Z）表示.例如Len（345）=3（位），Len（988667）=6（位），Len（0）=1（位）.

1 一组连续自然数的位数分析

先分析一组连续自然数中位数个数的计算公式.

定律1 对于给定的集合X=[x1，x2]（x1，x2∈N，x2≥x1），其中位数为n 的个数为：

式（1）中，S（xn）为X 中位数为n 的个数，n=[n1，n2]，n∈N；n1，n2分别为x1和x2的位数，n1=len（x1），n2=len（x2）.

证明 对于任意n 位数来说，当n=1 时，最小的n 位数为10n-1-1=0；当n>1 时，最小的n位数为10n-1，而最大的n 位数为10n-1.给定x1的位数n1=len（x1），当n=n1时位数的个数需从最大的n1位减去x1加1，即10n-1-x1+1=10n-x1（同样适合于n=1 的情况）；同理，当n=n2=len（x2）时位数的个数需要从x2减去最小位数，即x2-（10n-1+1）=x2-10n-1-1；当n1＜n＜n2时，n位数的个数为最大n 位数减去最小n 位数，即（10n-1）-（10n-1）+1=9×10n-1.

定律1 证毕！

2 两组连续自然数乘积的位数分析

设两组连续自然数集合为X=[1，x]（x∈N，x≥1），Y=[1，y]（y∈N，y≥1），其乘积S={（x，y）|x∈X，y∈Y，x*y}.我们下面分析S 中的各种数字位数的个数.可分为如下三种情况.

2.1 第一种情况：x，y 充分大

由于x＜∞，y＜∞都充分大，所以S 中包含了任意多的位数，对此有如下定律.

定律2 对于给定的连续自然数集合X=[1，x]，Y=[1，y]（x，y∈Z+），其乘积S={（x，y）|x∈X，y∈Y，x*y}中位数为n 的数字的个数为

式（2.1）中，S（n）为S 中位数为n（n∈N+）的个数，⎿x」为对实数x 向下取整的值；k（n）为参数，k（n）=10n-1，n 为所求的数字位数的编号.

证明 为了形象理解集合S={x*y} 中各种数字位数的分布情况，现引入一组如图1 所示的双曲函数族xy=k（n），其中k（n）=10n-1（n，x，y∈N+）.可以看出，S 中n 位数的个数，实际上可以转化为求不等式xy≤k（n）整数解的问题.

对于充分大的x 和y，S 中的1 位数为区间{x>0，y>0，xy≤9}内的整数点集合，2 位数为9＜xy≤99 内整数点集合，…，n 位数则分布于10n-1＜xy≤10n+1-1 区间内.图2 给出了所有1 位数的个数，即y≤9/x 的整数解的点阵分布；其余位数点阵分布同理.从而得出1 位数的个数为：

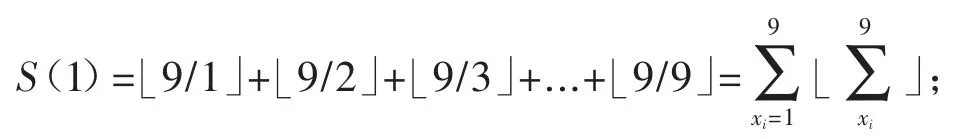
同样，1 位数和2 位数的总个数为y≤99/x 中整数解的集合，即

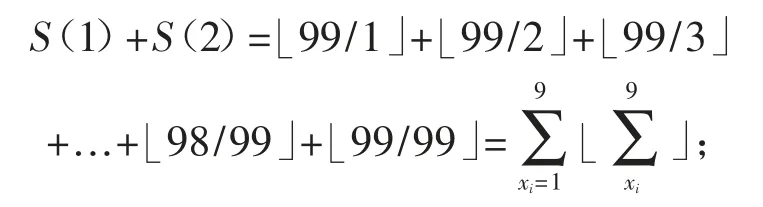
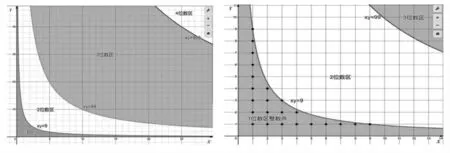
图1 双曲函数及数字位数区域示意图

图2 一位数整数点阵示意图

所以

定律2 证毕！

根据“向下取整”的定义，在公式（2.2）中，当xi>10n-1-1 时有⎿（10n-1-1）/xi」=0，所以，公式（2.2）也可表达成

例2 当x 和y 充分大时，求S=（1～x）*（1～y）中各种位数的个数.

解 把n=1，2，3…代入（1）式，求得k1=9，k2=99，k3=999，…，再分别求得S（1），S（2），…，如下：

同理可求出其他各种位数的个数，计算结果见表1.

表1 S 中各种位数计算结果

2.2 第二种情况：y=y0，x 充分大

这可看成y≤y0，x＜∞与双曲函数族的相交范围内各种位数的情况（见图3）.

图3 y=y0 与双曲族相交示意图

定律3 设X=[1，x]，Y=[1，y0]（x，y0∈N），其乘积S={（x，y）|x∈X，y∈Y，x*y，y≤y0}中位数为n 的数字的个数为：

定律3 证毕！

当给定x≤x0，y＜∞时，原理相同.有兴趣者可以试着给出计算公式.

2.3 第三种情况：x=x0，y=y0

定律4 设X=[1，x0]，Y=[1，y0]（x0，y0∈N），其乘积S={（x，y）|x∈X，y∈Y，x*y，x≤x0，y≤y0}中位数的种类和位数的个数为：

式（2.5）中，S（n）为S 中位数为n 的个数，n∈N+，⎿x」为对x 向下取整；m 为S 中最大位数，m=len（x0*y0），它同时也表示着S 中位数的种类；k（n）为参数，k（n）=10n-1，当k（n）>x0取k（n）=x0；x0i为y=y0与xy=k（n）的交点坐标向下取整的 值，x0i=⎿k（n）/y0」（i=1，2，3，…，m），当x0i＞x0时，取xi0=x0.

证明 引入双曲函数族xy=k（n），设y=y0与xy=k（n）交点向下取整分别为x01，x02，…，x0i，…，x0n，其中x0i=⎿k（n）/y0」（i=1，2，3，…，n），最大的位数为m=len（x0*y0），如图4 所示.显然，当位数n＜m 时，各种位数的个数计算公式与（2.3）基本相同，不同点只在于计算范围的变化，即当x0i＞x0或k（n）>x0时，取x0i=k（n）=x0，从而证得（2.5）式；当n=m 时，所有数字的个数等于集合S 的基数，即S（1）＋S（2）＋…＋S（m）=|S|=x0*y0，证得（2.6）式.

定律4 证毕！

图4 x=x0，y=y0 与双曲族相交示意图

例3 求S=（1～398）*（1～252）乘积中位数为5 和6 的数字的个数.

解 设x0=398，y0=252，其乘积S 的基数|S|=x0*y0=100296，最大位数m=len（|S|）=6 位，即S中共有6 种位数的数字.由k（n）=10n-1 得，k4=104-1＞x0，k5=105-1＞x0，故取k4=k5=x0=398，而y0=252 与xy=k（n）的交点集合为：x0i=⎿k（n）/y0」={⎿9/252」，⎿99/252」，⎿999/252」，…，⎿999999/252」={0，0，3，39，396，398}（注意x06＞x0，取x06=x0=398），由公式（2.5）得：

需要指出，对于X=[x1，x2]与Y=[y1，y2]（x1，y1，x2，y2∈N，x2≥x1≥1，y2≥y1≥1） 的乘积S 的位数计算，可先按照公式（2.5）求出S（i）={（x，y）|x∈X，y∈Y，x*y，x≤xi，y≤yi}（i=1，2）中各种位数的个数，再由公式S（n）=S（2）-S（1）求出S中各种数字的位数，这里不再赘述.

致谢：本文英文部分的翻译工作得到了陈钟同志的帮助，在此表示感谢！