龙汉青,　于克凡,　张必成

(湘潭大学 数学与计算科学学院, 湖南 湘潭 411105)

图的连通度是图论中的基本研究对象. 有许多方式去强化这个概念, 比如要求哈密顿性,k-连 通性, 限定直径的值,等等. 一种有趣的强化——彩虹连通, 在2008年首先由Chartrand G等学者在[1]中提出. 这个新概念来自政府与下级机构间的信息传输. “911”事件等致命袭击的一个意想不到的后果是使得执法机构和情报机构无法通过正常渠道相互沟通.为了保护涉及国家安全的信息,同样需要保证部门之间能够准确通讯.这两方面的问题可以通过设计部门间的信息传输通道(可能需要其他部门作为中间传输者)来解决.这需要大量的密码以抵御网络入侵者.为了便于管理,密码又需尽可能的少.保证部门间通信渠道所需要密码均两两不同的最小密码数是多少？这个问题可以通过图论语言来描述.用顶点代表机构,边代表机构间的沟通渠道,把所得到的图记为G.用不同颜色代表不同密码,则所要求的最小密码数就是图G的彩虹数cr(G).

我国学者李学良教授的团队在图的彩虹连通方面做了大量的研究,他们研究了稠密图[2],3-连通图[3],直径为2的图[4]等一系列图的相关性质.图的彩虹数与其他参数,比如最小度,连通控制数,连通度之间的联系以及图与其线图,补图的彩虹数的关系在[5]～[9]中被研究.更详细的内容可参见综述文章[10].

作为无向图的彩虹连通的推广,有向图的彩虹连通这一概念由Dorbec P等学者于2014年在[11]中提出.有向图的彩虹连通方面的研究工作较少.[11]和[12]分别研究了竞赛图和循环有向图的彩虹连通.

在本文中我们考虑直径为2的有向图的彩虹连通.

为了方便起见,下面介绍一些必要的概念.本文未提及的符号和术语与[13][14]一致.

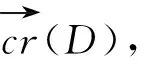
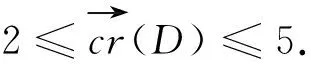
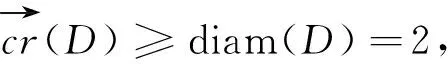
设D={V,E}是直径为2的有向图,对任意给定顶点v∈V,令N1:=N+(v)N-(v),N2:=N+(v)∩N-(v),N3:=N-(v)N+(v).令顶点集V的子集R满足R=V({v}∪N1∪N2∪N3).如图1所示,将E(v,V)和E(V,v)中的弧分别着颜色1和5；E(R,N1∪N2∪N3)和E(N1∪N2∪N3,R)中的弧分别着颜色3和2；弧集E(N2,N3),E(N1,N2),E(N1,N3)中的弧分别着颜色2,3和4；D[N1],D[N2],D[N3],D[R]中的弧分别着颜色5,4,1,5；剩余的弧用颜色1,2,3,4,5任意着色.

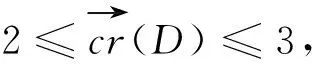
定理2设k-正则有向图D={V,E}的直径为2,那么

如果k2≤2μ1-4,那么

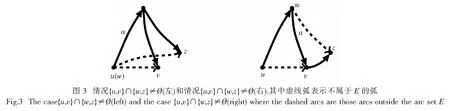
注意到对于具有参数(n,k,μ,λ,t)的有向强正则图D,μ1(D)=μ2(D)=μ.

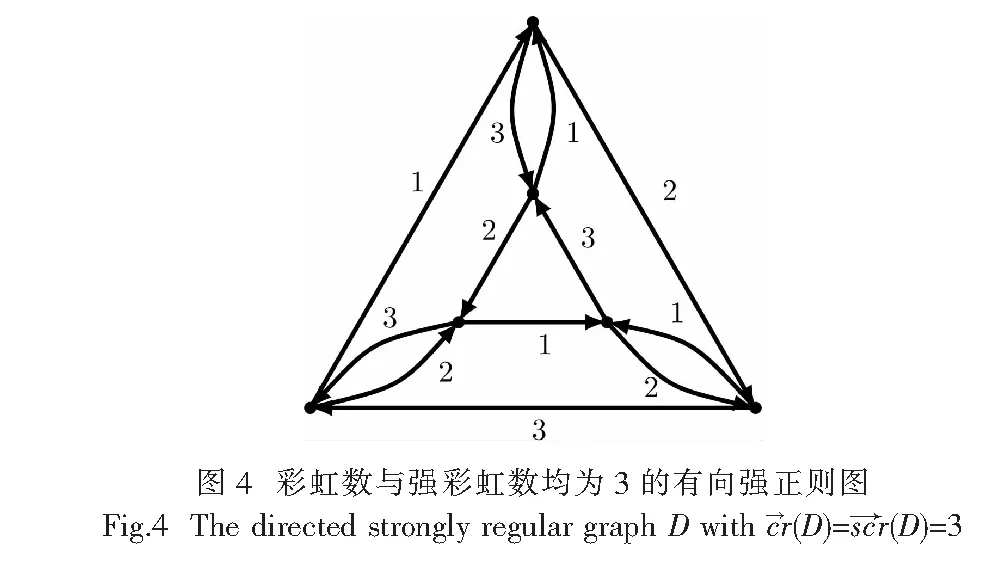
如图4中的有向图为6阶的有向强正则图D,它的参数集(n,k,μ,λ,t)=(6,2,1,0,1).注意到该图仅使用两种颜色的彩虹着色,如果存在,一定是强彩虹着色,而在这样的强彩虹着色下,由μ=1知“外围三角形”一定是“彩虹”的,与着色仅使用两种颜色矛盾,故D的彩虹数至少为3,实际上D的彩虹数与强彩虹数皆为3,图4给出了一种仅用3种颜色的强彩虹着色.

[1]CHARTRAND G, JOHNS G L,MCKEON K A ，et al.Rainbow connection in graphs[J].Mathematica Bohemica,2008,133(1):85-98.

[2]LI X, LIU M,SCHIERMEYER I. Rainbow connection number of dense graphs[J].Discussiones Mathematicae Graph Theory,2013，33(3):603-611.

[3]LI X,SHI Y. Rainbow connection in 3-connected graphs[J]. Graphs and Combinatorics,2013,29(5):1471-1475.

[4]LI H, LI X,LIU S.Rainbow connection of graphs with diameter 2[J].Discrete Mathematics,2012,312(8):1453-1457.

[5]KRIVELEVICH M, YUSTER R.The rainbow connection of a graph is (at most) reciprocal to its minimum degree[J].Journal of Graph Theory,2010,63(3):185-191.

[6]SUNIL CHANDRAN L,DAS A, RAJENDRAPRASAD D,et al.Rainbow connection number and connected dominating sets[J].Journal of Graph Theory,2012,71(2):206-218.

[7]LI X,LIU S, CHANDRAN L S,et al.Rainbow connection number and connectivity[J].The Electronic Journal of Combinatorics,2012,19(1):20.

[8]LI X, SUN Y.Rainbow connection numbers of line graphs[J].Ars Comb,2011,100:449-463.

[9]CHEN L, LI X, LIAN H. Nordhaus-gaddum-type theorem for rainbow connection number of graphs[J].Graphs and Combinatorics,2013:1-13.

[10]LI X,SHI Y, SUN Y.Rainbow connections of graphs:a survey[J].Graphs and Combinatorics，2013:1-38.

[11]DORBEC P,SCHIERMEYER I, SIDOROWICZ E,et al.Rainbow connection in oriented graphs[J].Discrete Applied Mathematics,2014,179:69-78.

[12]ALVA-SAMOSJ,MONTELLANO-BALLESTEROS J J. Rainbow connection in some digraphs[J].Graphs and Combinatorics，2016,32(6):2199-2209.

[13]BONDY J A,MURTY U S R. Graph theory with applications[M].Citeseer,1976：290.

[14]DUVAL A M.A directed graph version of strongly regular graphs[J].Journal of Combinatorial Theory, Series A,1988,47(1):71-100.

[15] ALON N, SPENCER J H.The probabilistic method[M]. John Wiley & Sons, 2004.