林上为，吴姝煜

（山西大学 数学科学学院，山西 太原 030006 ）

0 引言和术语

对于这里没有定义的图论术语和符号，请参见文献［1］。本文讨论的有向图都是有限的且没有环和多重弧。对有向图D，用V=V(D)和A=A(D)分别表示D的顶点集和弧集。对有向图D中的一个顶点v，它的外邻域为N+(v)={u∈V(D)：vu∈A(D)}，出度为

D的最小出度是

点v的内邻域N－(v)，入度d－(v)和D的最小入度δ－(D)可类似定义。顶点v的度定义为d(v)=min {d+(v)，d－(v)}，有 向 图D的 最 小 度 定 义 为δ(D)=min {d(v)：v∈V(D)}=min {δ+(D)，δ－(D)}。对于非空顶点子集对X，Y和D的弧子集S，记S(X，Y)={xy∈S：x∈X，y∈Y}。若Y=Xˉ，则用A+(X)或者A－(Y)表示

若有向图D中任意两个顶点互相可达，那么称有向图D是强连通的。约定只有一个顶点的有向图是强连通的。称有向图D的极大强连通子图为D的强连通分支。一个强连通分支是平凡的，如果它只包含一个顶点。对强连通有向图D，称S⊆A(D)是有向图D的一个弧割，如果D－S是不强连通的。有向图D的一个最小弧割的弧数称为D的弧连通度，记为λ(D)。

众所周知，当用有向图为有向互联网络建模时，有向图的弧连通度越大，对应网络越可靠。且对所有有向图D都有λ(D)≤δ(D)成立，称满足λ(D)=δ(D)的强连通有向图D为极大弧连通的。极大弧连通有向图的充分条件曾得到广泛的研究[2]。特别地，文献［3］给出极大弧连通图的一个度条件。

定理1[3]设D是一个n阶有向图。若所有满足uv∉A(D)的点对{u，v}都有

则D是极大弧连通的。

文献［4］给出另外一种类型的度条件。

则有向图D是极大弧连通的。

为了将Esfahanian 和Hakimi[5]提出的无向图的限制边连通度推广到有向图，Volkmann[6]引入了限制弧连通度的概念。设D是一个强连通有向图。称D的一个弧割S是D的一个限制弧割，如果DS有一个非平凡的强连通分支D1使得D－V(D1)包含一条弧。如果强连通有向图D中存在一个限制弧割，则称D是λ′-连通的。一个λ′-连通有向图D的限制弧连通度λ′(D)是D的一个最小限制弧割所含的弧数。

2008 年，Wang 和Lin[7]在研究限制弧连通度上界时引进弧度的概念。对有向图D的一条弧xy，记

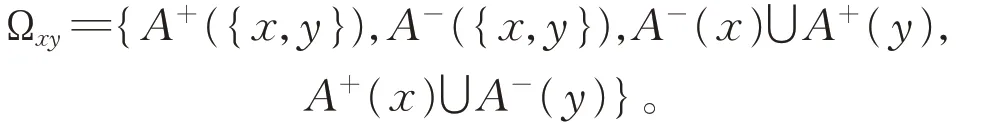
将弧xy的弧度定义为ξ′(xy)=min {|S|：S∈Ωxy}，有向图D的最小弧度定义为

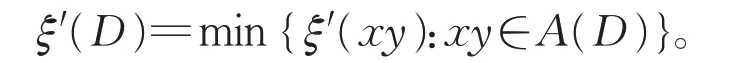
文献［7］也证明了以下结果。

定理3[7]设D是一个满足δ+(D)≥3 或者δ－(D)≥3 的强连通有向图，那么有向图D是λ′-连通的且λ′(D)≤ξ′(D)。

2013 年，Balbuena 等[8]证 明 了 一 个 类 似 的结果。

定理4[8]设D是阶数至少为4 的强连通有向图。如果D的最小度δ(D)≥2，那么D是λ′-连通的且λ′(D)≤ξ′(D)。

由定理3 和定理4 可知对大多数有向图D，最小弧度ξ′(D)是限制弧连通度λ′(D)的上界。据此，文献［7］引入了极大限制弧连通图的概念。称一个λ′-连通有向图D是极大限制弧连通的，如果λ′(D)=ξ′(D)。近年来，限制弧连通度得到了一些研究［9-12］，这其中极大限制弧连通有向图的充分条件尤其受到关注，比如度条件［13-17］，直径围长条件[18]和邻域条件[19]。特别地，文献［7］也证明了极大限制弧连通有向图的一个邻域交条件。与定理1 同样考虑，可由邻域交条件得下面的度条件。

定理5[7]设D是一个n阶有向图。若所有满足uv∉A(D)的点对{u，v}都有

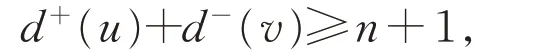
则D是极大限制弧连通的。

本文将沿定理2 的思路，给出与定理5 不同的极大限制弧连通有向图的一个度条件。在最后也给出例子说明本文得出的结果与定理5 的结果是独立的并且在某种意义上本文所得的结果是最优的。

1 极大限制弧连通有向图的度条件

在给出主要结果之前，先介绍两个引理。由文献［8］中定理1.2 的证明可得下面的引理1。

引 理1[8]设D是 一 个 满 足λ′(D)≤ξ′(D)的λ′-连通有向图，且设S是D的一个最小限制弧割，那么要么存在一个顶点子集X⊆V(D)使得导出子图D[X]和D[V－X]中都至少包含一条弧且S=A+(X)，要 么 存 在 一 条 弧uv∈A(D) 使得S∈Ωuv。

引理2 设D是一个阶数为n≥4 的强连通有向图。若除可能的一个点外，D的所有顶点的度都至 少 为 3，则 有 向 图D是λ′- 连 通 的 且λ′(D)≤ξ′(D)。

证明 对任意给定的一条弧xy∈A(D)，因为除可能的一个点外，D中所有顶点的度都至少为3，所以除可能的一个点外，D－{x，y}中所有顶点的度都至少为1。这说明D－{x，y}包含一个圈。因此，D－{x，y}有一个非平凡的强连通分支D1。对任意的S∈Ωxy，D1也是D－S的一个非平凡的强连通分支并且D－V(D1)含弧xy。这说明S是一个限制弧割，从而D是λ′-连通的并且λ′(D)≤|S|。由弧xy的任意性和S的任意性可得λ′(D)≤ξ′(D)。

则D是极大限制弧连通的。

证明 因为对任意的u∈V(D)都有d(u)≤n－1，所以除可能的一个点外，满足题设条件的D的所有顶点的度都至少为

由引理2，D是λ′-连通的且λ′(D)≤ξ′(D)。用反证法，假设D不是极大限制弧连通的，则有λ′(D)＜ξ′(D)。设S是D的一个最小限制弧割。若存在一条弧xy使得S∈Ωxy，则λ′(D)=|S|≥ξ′(D)，矛盾。因此，由引理1，存在一个顶点子集X⊆V(D)使得D[X]和D[Y]都包含至少一条弧且S=A+(X)，其中Y=V(D)－X。显然，|X|≥2。若|X|=2，则可设X={x，y} 且xy是 一 条 弧。此 时S=A+(X)=A+({x，y})∈Ωxy。从而，

λ′(D)=|S|=|A+({x，y})|≥ξ′(D)，矛盾。

因此，|X|≥3。同理可得|Y|≥3。记p=|X|和q=|Y|。不失一般性，假设p≤q。

设Y′={y∈Y： 存 在 一 个 顶 点y′∈Y使得{y，y′}∈π(D)}，Yi={y∈Y：存在一个顶点x∈Xi使得{x，y}∈π(D)}，i=0，1，2，3，4。 显 然有

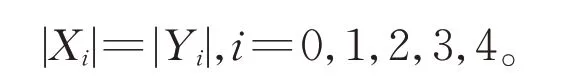
对任意的i∈{0，1，2，3}和y∈Yi，存在一个顶点x∈Xi使得{x，y}∈π(D)，因此

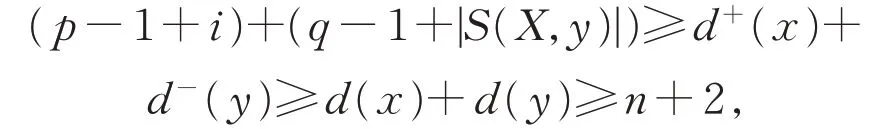
整理得|S(X，y)|≥4－i，从而有|S(X，Yi)|≥(4－i)|Yi|=(4－i)|Xi|。因此

将（2）式和（3）式相加，得到

对两个互相配对的顶点x，x′∈X′，有

记

则

记|Y′|=2t，同理可得

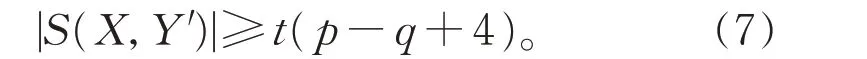
若n是偶数，则D中所有点都是配对点，因此

设x1，x2是X中一对顶点，使得x1和x2之间有弧且|S(x1，Y)|+|S(x2，Y)|最小。记

下面对k的取值分情况讨论，得到想要的矛盾。

情形1k≤2。

此 时，ξ′(D)≤|A+({x1，x2})|=A({x1，x2}，|X－{x1，x2})|+|S(x1，Y)|+|S(x2，Y)|≤2|X－{x1，x2}|+|S(x1，Y)|+|S(x2，Y)|=2(p－2)+|S(x1，Y)|+|S(x2，Y)|=2(p－2)+k≤2(p－1)。结 合（8）式 有λ′(D)≥ξ′(D)，与 假 设λ′(D)＜ξ′(D)矛盾。

情形2k≥3。

不妨设|S(x1，Y)|≤|S(x2，Y)|。设

则有

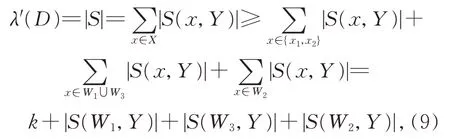
和

对任意的x∈W1∪W3，有弧x1x。由x1x2的选取有

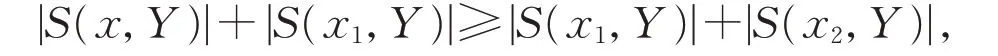
由此可得对任意的x∈W1∪W3，

同 理，对 任 意 的x∈W2，有|S(x，Y)|+|S(x2，Y)|≥|S(x1，Y)|+|S(x2，Y)|，由此可得对任意的x∈W2，

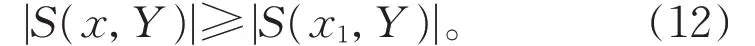
情形2.1 |S(x1，Y)|≥1。

若|S(x1，Y)|=1，则

|S(x2，Y)|=k－|S(x1，Y)|≥3－1=2。

若|S(x1，Y)|≥2，则

|S(x2，Y)|≥|S(x1，Y)|≥2。

综上都有|S(x2，Y)|≥2。

由（11）式和（12）式可知，对任意的x∈W1∪W3有|S(x，Y)|≥|S(x2，Y)|≥2，且 对 任 意 的x∈W2有|S(x，Y)|≥|S(x1，Y)|≥1。再结合（9）式和（10）式可得λ′(D)≥k+2|W1|+2|W3|+|W2|≥k+|W1|+|W2|+2|W3|≥ξ′(D)，矛盾。

情形2.2 |S(x1，Y)|=0。

此时|S(x2，Y)|=k。结合（9）式和（11）式有

由（8）式可得

结合（10）式、（14）式和假设可得

整理得

结 合（10）式、（13）式 和 假 设 可 得k+|W1|+|W2|+2|W3|≥ξ′(D)＞λ′(D)≥k+k|W1|+k|W3|，整理得

结合（15）式和（16）式有

由此可得

这 说 明N+(x1)∩(X－{x1，x2})=∅， 又 由|S(x1，Y)|=0，故N+(x1)⊆{x2}，从而d+(x1)≤1。

由（17）式可知，W2≠∅，若W2中一点x′1使得|S(x′1，Y)|=0， 则x2x′1是 一 条 弧 ， 且|S(x′1，Y)|+|S(x2，Y)|=k，同上面对x1，x2的讨论可得d+(x′1)≤1，此时图D中有两个度小于等于1的顶点x1和x′1，与（1）矛盾。因此，对W2中任意一点x′1都有|S(x′1，Y)|≥1。再结合（9）式、（10）式和（18）式 可 得λ′(D)≥k+|W2|≥ξ′(D)，与 假 设λ′(D)＜ξ′(D)矛盾。定理得证。

2 对结果的讨论

则称有向图D具有性质Pk。定理2 表明，若一个有向图具有性质P0，则该图是极大弧连通的。本文证明了每个满足性质P2的有向图都是极大限制弧连通的。下面用例子说明，由性质P1不能推出极大限制弧连通性，因此定理6 在某种意义上是最优可能。

例1 设U={u1，u2，···，up}，

是基数都为p的4个不相交集合，其中p≥3。设H1和H2是 顶 点 集 分 别 为V(H1)=U∪X和V(H2)=V∪Y的两个完全无向图。设H3是具有二划分(U，V)的1-正则二部无向图并且设H4是具有二划分(X，Y)的 2- 正 则 二 部 无 向 图 。 设G是 并 图H1∪H2∪H3∪H4，设有向图D是图G的完全双定向。 对 任 意 的 一 个 点 对{u，v}∈{{u1，y1} ，{u2，y2} ，…，{up，yp} ，{v1，x1} ，·· ·，{vp，xp} }都有

d(u)+d(v)=2p+(2p+1)=|V(D)|+1，因此D具有性质P1。但是A+(U∪V)是一个限制弧割，从而有