刘 邓

(江汉大学，武汉 430010)

广义积分上的一致收敛问题

刘 邓

(江汉大学，武汉 430010)

文章主要讨论并总结含参变量的广义积分以及一些常规的判别法，展示并举例了Cauchy判别法﹑M判别法﹑Dirichlet判别法﹑Abel判别法﹑微分法﹑级数判别法以及含参量广义积分的Heine定理在实际问题中的运用，同时对各个判别法进行了详细的阐述并对其优缺点简要的说明与归纳，希望对读者们有所帮助。

广义积分；一致收敛;判别法

我们知道定积分有两个最重要且最基础的限制：①积分区间的有穷性；②被积分函数的有界性,而广义积分是突破其限制的推广，当积分的有穷区间变为无穷区间，我们便得到了无穷积分，而当被积函数有界变为无界时，我们便得到了无界积分，也称为瑕积分。生活中面临的大多数实际问题经常会突破有限或有界的限制，因此广义积分便有了诞生的意义和必要。由于许多广义积分的计算非常困难，于是人们希望通过对其性质的判断来为计算带来方便，其中敛散性的判别尤其重要。

在实际生活中，自然条件远比人为假设要复杂的多，故含参量广义积分的应用范围要比非含参量广义积分的应用范围要广阔的多，而含参量广义积分的计算相应的更为的复杂。而为了方便人们去计算这类积分，我们希望广义积分和被积函数所具备性质更加优化，故广义积分上的一致收敛就是人们所关注的。

首先我们给出含参量广义积分以及一致收敛的两个具体概念。

统一规定下面的I都表示实数轴上的区间，且区间没有有限或无限的限制。

定义1设f(x,y)R=[a,∞]×I上，若对∀yI，广义积分都收敛，则它是y在I上函数，记作I(y)，即：

I(y)称为含参数yI的无穷积分，也就是我们所说的含参量广义积分。

定义2若对∀ε>0，∃A0=A0(ε)，(A0c)，当A',A≥A0时，对一切yI，成立：

一、一致收敛的充要条件

我们可以直接通过定义2，得出如下直接判断一致收敛的方法。

解因为对充分大的M>0时，有：

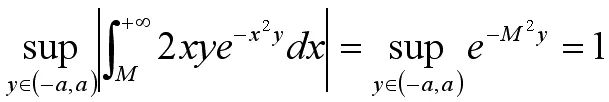
二、Cauchy判别法

定理1 设f(x,y)与F(x,y)定义在无界区域R=[a,∞]×I上.如果存在a'>a使得：

很明显，当目标积分中的某部分可以与 的幂函数组成常用的积分时，使用 判别法可以将有效的对原积分进行处理，确定后续的验证方向。

三、M判别法

设有函数g(y)，使得

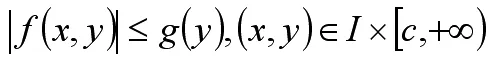
M判别法类似于夹逼定理，通过与一些常见积分进行比较，可以快速判定原积分.注M判别法得到的结论是绝对一致收敛，但不是绝对一致收敛就能用M判别法来判断。

四、Dirichlet判别法

参照级数的Dirichlet判别法，将原积分看做两个单独的积分，且对两个新的积分要求和级数Dirichlet判别法十分相似。

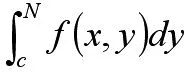
对参量x在I上一致有界，既∃M，(M>0)，对∀N>c及x∈I∀ ，有

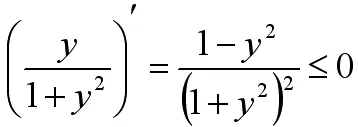
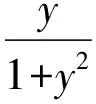
五、Abel判别法

参照级数的Abel判别法，将原积分看做两个单独的积分，且对两个新的积分要求和级数Abel判别法十分相似。

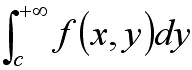
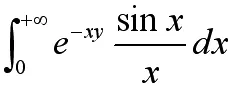
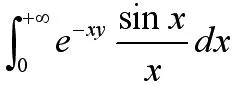
我们可以看到Dirichlet判别法与Abel判别法的运用方法都是将目标积分拆分成两个我们熟悉的积分，在运用这两种方法对其进行判定。

六、微分法

当给出y在其取值范围内可微且在范围内使得原积分收敛时，我们可以通过求其偏导对原积分是否一致收敛进行判定。

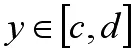
我们可将定理3中的条件1)放宽，将条件2)变强.得如下定理：

七、级数判别法

通过教材[2]，我们可以知道含参变量反常积分的一致收敛与函数项级数的一致收敛是有一定联系的，所以相应的可以通过函数项级数来帮助对含参量反常积分的判定。

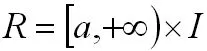
八、含参量广义积分的Heine定理

Heine定理也被称之为归结原理，在函数极限与数列之间起到相互关联的作用，同时可将Heine定理的应用通过函数项级数向含参量积分做出推广。

证明必要性，定理5可直接证明其必要性。

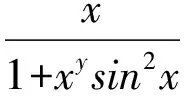
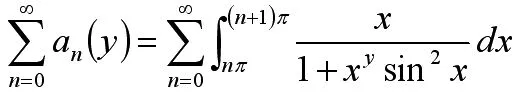
令x=nπ+t，得

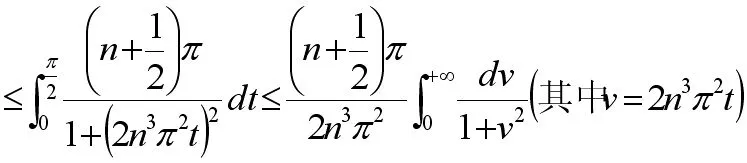
[1]华东师范大学数学系.数学分析：上册[M].北京：高等教育出版社，2010.

[2]华东师范大学数学系.数学分析：下册[M〗北京：高等教育出版社，2010.

[3]董立华, 叶盼盼. 关于含参量广义积分一致收敛性的讨论[J]. 枣庄学院学报, 2008, 25(5):51-55.

[4]赵文强. 关于含参量广义积分一致收敛性的教学研究[J]. 重庆工商大学学报:自然科学版, 2011, 28(5):458-462.

[5]王秀红. 含参变量广义积分一致收敛的Heine定理[J]. 烟台师范学院学报:自然科学版, 2003, 19(4):305-307.

[6]谢胜利. 含参变量广义积分与瑕积分一致收敛的一个判别法[J]. 荆州师专学报, 1982(2)：74-78.

[7]吴传生. 含参变量的Fuzzy值函数广义积分一致收敛性[J]. 武汉工学院学报, 1990(1):47-56.

[8]郭小春. 含参变量的广义积分非一致收敛的一个判定定理[J]. 宜春学院学报, 2008, 30(S1):156-157.

[9]薛访存. 函数项级数一致收敛定理的证明和广义积分收敛的充要条件[J]. 嘉应学院学报, 2003, 21(6):19-22.

[10]张庆政. 一致收敛的二元函数与含参量广义积分的两个性质[J]. 黄淮学刊:自然科学版, 1990(S4):66-71.

[11]郝勇. 收敛的广义积分被积函数趋于零的条件[J]. 信阳师范学院学报：自然科学版, 1987(1)：74-76+73.

[12]刘德祥, 刘绍武. 关于级数和积分非一致收敛的一个充分条件[J]. 哈尔滨师范大学自然科学学报, 1995(1):29-32.

[13]刘勇. “一致收敛”概念的推广及其应用[J]. 内蒙古财经大学学报, 2013, 11(5):140-142.

[14]郑德印. 一致连续与一致收敛概念的统一[J]. 南都学坛, 1993(S3):41-42.

[15]张英琴. 非一致收敛的几个判别定理[J]. 广东石油化工高等专科学校学报, 1996(1)：65-69.

[16]陈争鸣, 施伟民. 含参量广义积分连续性的充分条件[J]. 三明学院学报, 2008, 25(4):377-378.

[17]裴礼文，数学分析中的典型问题与方法(第二版)[M].北京：高等教育出版社，2006.

Uniformconvergenceingeneralizedintegrals

Liu Deng

(JianghanUniversity,Wuhan430010,China)

In this paper, we mainly discuss and summarize containing parameter improper integral and some conventional discriminant method, display and an example of a discriminant method, discriminant analysis, discriminant analysis, discriminant analysis, differential method, series method and application of Heine theorem of generalized parametric integrals in the practical problems with. At the same time, each of the discriminant method is described in detail and its shortcomings are briefly described and summarized, and they hope to help readers.

generalized integral；uniform convergence;discrimination method

O141

A

1673-3878(2017)05-0022-05

2017-05-16

刘邓(1994—)，男，湖北武汉人，江汉大学数学与计算机科学学院硕士研究生；主要研究方向：广义积分.