刘莹莹，罗 勇，胡亦郑

(温州大学数学与信息科学学院，浙江温州 325035)

一类乙肝病毒传播的动力学模型研究

刘莹莹，罗 勇，胡亦郑

(温州大学数学与信息科学学院，浙江温州 325035)

根据乙肝病毒性肝炎（HBV）预防接种后出现的免疫逃避现象，且这种免疫逃避因年龄段不同而出现差异，本文考虑了具有阶段结构和连续预防接种的SIRS传染病模型．此模型把人群分为幼年和成年两个阶段结构；疾病采用标准发生率，在幼年和成年群体中均可传播，且只考虑对幼年群体进行连续预防接种，进而研究这种模型的渐近性态．在连续预防接种且不考虑垂直传染的情况下，得到此传染病模型的基本再生数R0，利用Routh-Hurwitz准则分别证明无病平衡点和正平衡点的局部稳定性，并选取合适的参数进行数值模拟．

乙肝病毒；免疫逃避；阶段结构；Routh-Hurwitz准则

传染病（Infectious Diseases）是由病原微生物和寄生虫等感染人体后产生的有传染性的疾病．在众多传染病中，乙肝病毒性肝炎（HBV）已经成为最严重也是最受世界关注的传染性疾病，对其动力学模型进行分析，预测其流行规律和发展趋势，寻求对其预防和控制的最优策略，已成为全世界医学界共同研究的课题之一．1927年Kermack和Mckendrick给出了经典的“SIR”舱室模型[1]，将总人口分为易感者（S），染病者（I）和恢复者（R）三类，众多学者在此基础上对传染病模型进行改进[2-4]，如考虑垂直传染发生率为标准型β/SIN的SIR模型[2]，考虑垂直传染和免疫逃避且采用指数输入的SIRS预防接种模型[3]．

对于具有阶段结构的传染病模型，周毅等考虑了一类分年龄阶段的流行病模型[4]如下：

其中S1为幼年易感者，I1为幼年染病者，S2为成年种群．考虑疾病只在幼年群体（无生育能力）中传播，讨论了其无病平衡点和正平衡点的存在及全局稳定性，给出疾病流行与否的阈值．

于宇梅等考虑一类具有阶段结构的SIRS传染病模型[5]：

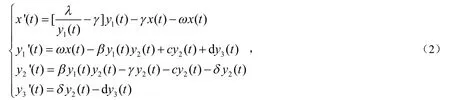
其中x(t),y1(t),y2(t),y3(t)分别代表幼年个体、成年易感者个体、成年染病者个体和成年康复者个体在t时刻的数量．考虑疾病仅在成年个体传播，而幼年个体不感染此传染病，分析得到传染病消亡与否的阈值，并证明了无病平衡点和正平衡点的稳定性．

前人对于具有阶段结构的传染病模型的研究，大多只考虑疾病仅在幼年群体中或者疾病仅在成年群体中传播，没有考虑疾病在两个年龄段均可传播的特殊情况．本文在众多学者传染病模型研究基础上[3-6]，考虑到乙肝病毒性肝炎（HBV）在整个人群结构中均可传播，且在不同的年龄段免疫逃避的情况有所不同，给出一类具有阶段结构和免疫逃避的SIRS传染病模型．

1 模型的建立

目前乙肝病毒性肝炎（HBV）的防控工作，采取的有效策略就是接种乙肝疫苗[6]，但免疫逃避的出现又为乙肝的防控工作提出了新的难题．本文采用标准发生率，把人群分为幼年和成年两个阶段结构，且该传染病在这两个年龄段中均可传播；不考虑垂直传染，即假定所有新生儿均为易感者，且只对幼年易感者进行连续预防接种，接种后从易感者类移出变为恢复者，康复者或接种者逐渐失去免疫力又变为易感者类，建立一类具有阶段结构和免疫逃避且发生率为标准型的HBV传染病模型如下：

其中总人口N=S1+S2+I+R ，则有

其中S1和S2分别表示幼年易感者类和成年易感者类，I为感染者类，R为恢复者类，b为出生率，这里不考虑母婴或父婴垂直传播；β为接触率，这里采用标准发生率；p为连续预防接种率，k为从幼年群体到成年群体的转移率，μ为自然死亡率，α为因病死亡率（这里假设b≥α），γ为从染病者到恢复者的转移率，ξ为免疫失去率．

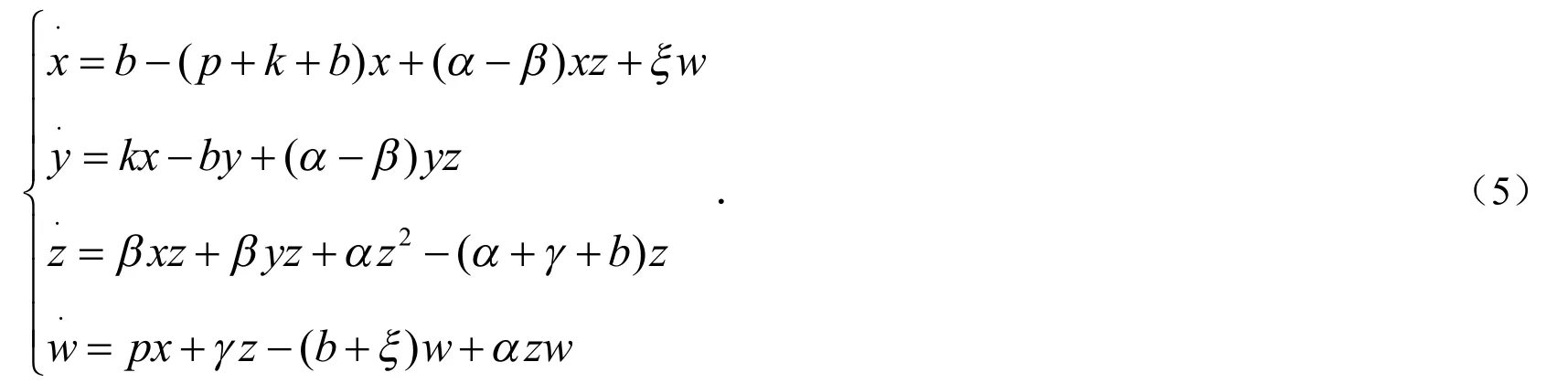
容易得出对于系统（5）来说，区域Ω={x≥0,y≥0,z≥0,w≥0,x+y+z+w=1}为正向不变集，即系统的可行域，Ω0=Ω-∂Ω，其中∂Ω为可行域Ω的边界．由于没有解可以离开区域Ω的边界，不失一般性，下面在可行域Ω内研究系统（5）．

2 模型分析

2.1 平衡点的存在性

令系统（5）的每个方程右端均为零，又由x+y+z+w =1，当z=0，易得模型（5）总存在无病平衡点E0=(x0,y0,0,w0)，其中，．由文[12]可计算系统（5）的基本再生数[12]为：

定理1 当R0＜1时，模型（5）只有无病平衡点E0，没有地方病平衡点；当R0＞1时，则模型除无病平衡点E0外，还存在唯一的地方病平衡点E+（x*,y*,z*,w*）．其中：

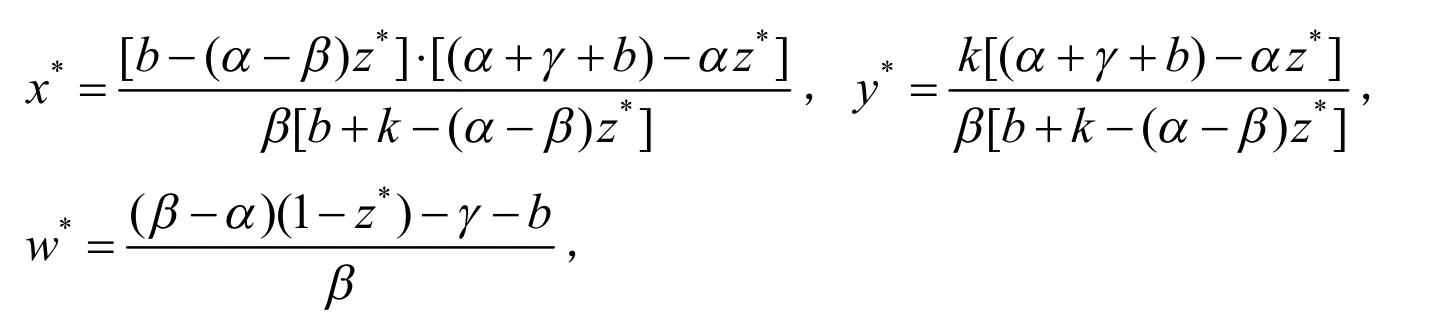
这里*z是三次方程（15）的唯一正根．

证明：令f1，f2，f3，f4分别代表系统（5）中第一、第二、第三、第四右端的表达式，令f1，f2，f3，f4均为零，当z=0时，由f1=0，f4=0可得．则易得：

又由f2=0可得．由此可知，模型（5）总存在无病平衡点．

当z≠0时，又由x+y+z+w=1可得：

f1(x,z,w)=b-(p+k+b) x+(α-β)xz+ξw=0，

f2(x,y,z)=kx-by+(α-β)yz=0，

其中β-α＞0，因为若β-α≤0，则由（14）式可知必有w＜0，不符合题意；且考虑实际情况，接触率β应该大于因病死亡率α，由w＞0可得，β-α-γ-b ＞0，这里假设b≥α．

当R0＞1时，有F(0)=D＞0，F(1)=A+B+C+D＜0，且有A＞0，B＜0，C＜0，D＞0，由Descartes符号法则[11]可知三次方程（15）在(0,1)上存在唯一的正解，记为z*，而当R0＜1时方程（15）在(0,1)上不存在正解，此时系统（5）只存在无病平衡点E0．

综上，当R0＞1时，系统（5）除无病平衡点E0外，存在唯一正平衡点E+(x*,y*,z*,w*)，其中，

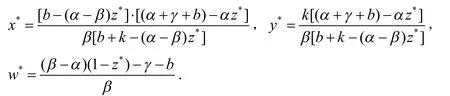
2.2 无病平衡点的稳定性

定理2 对于系统（5）的无病平衡点E0，当R0＜1时，无病平衡点E0是局部渐近稳定的；当R0＞1时E0是不稳定的．

证明：已知系统（5）在无病平衡点E0处的Jacobin矩阵为：

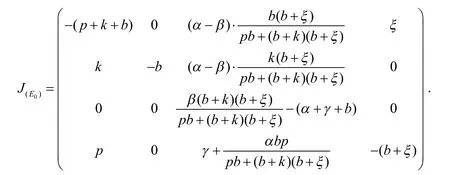
则此Jacobin矩阵所对应的特征方程为：

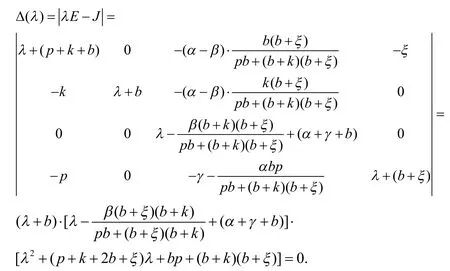
易知λ1＜0，当基本再生数R0＜1时，λ2＜0，而对于多项式方程

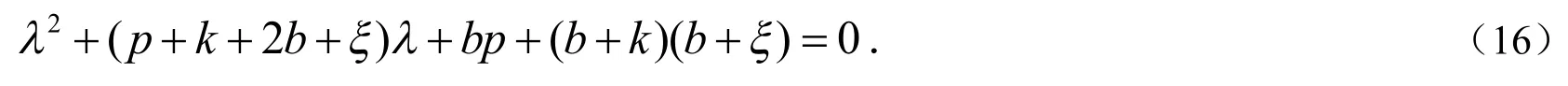
因为p+k+2b+ξ＞0，bp+(b+k)(b+ξ)＞0．则由Routh-Hurwitz准则可得：当R0＜1时，多项式方程的所有特征根均有负实部．则系统（5）的无病平衡点E0是局部渐近稳定的；当R0＞1时，λ2＞0，特征根不全为负，无病平衡点E0不稳定．

2.3 地方病平衡点的稳定性

定理3 当R0＞1时，系统（5）除无病平衡点E0外还存在唯一正平衡点E+(x*,y*,z*,w*)，且此正平衡点在Ω0内是局部渐近稳定的．

证明：当R0＞1时，由定理1可知系统（5）除无病平衡点E0外还存在唯一地方病平衡点E+．

以下证明其局部渐近稳定性．

由于x+y+z+w =1，则以y=1-x-z-w 替换系统（5）中的y，只考虑以下系统正平衡点E(x,z,w)的稳定性即可．

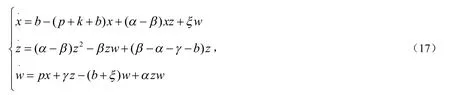
由于系统（17）存在唯一正平衡点E(x,z,w)，且系统（17）在此正平衡点的Jacobin矩阵为：

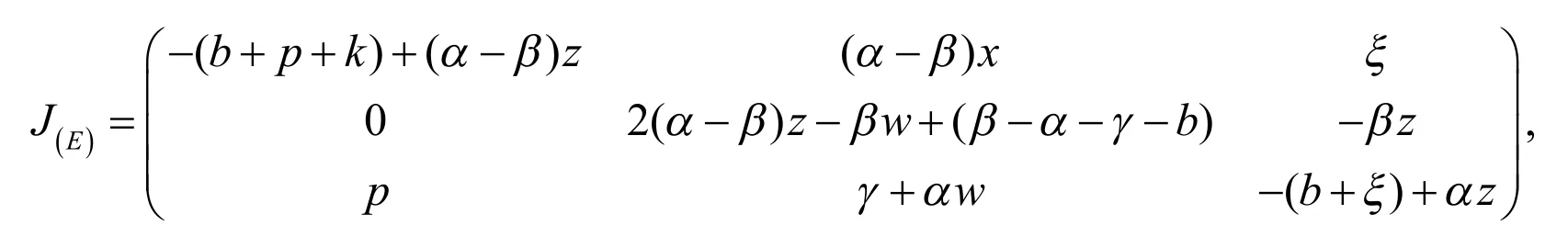
则此Jacobin矩阵的特征方程为：

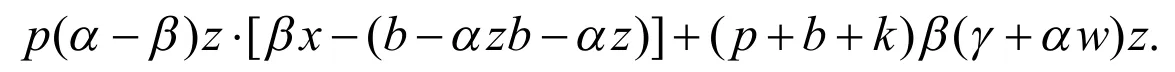
由于β-α＞0,b ≥α，则有H1＞0,H2＞0，又当R0＞1时，此Jacobin矩阵的特征方程有：

因此由Routh-Hurwitze定理可得：特征方程λ3+H1λ2+H2λ+H3=0的全部特征根均具有负实部，即系统（17）的正平衡点E(x,z,w)是局部渐近稳定的．由于系统（17）是由系统（5）降维得到的，在正平衡点处具有相同的稳定性，进而推广可得，系统（5）的正平衡点E+(x*,y*,z*,w*)在R0＞1时也是局部渐近稳定的．

3 数值模拟

以上分析了模型无病平衡点的局部稳定性，以及正平衡点的局部稳定性．为了观测本文模型在平衡点处的全局稳定性，选定合适的参数进行数值模拟．

令参数b=0.5,β=0.09,ξ=0.01,k =0.1,α=0.02,γ=0.04,p=0.05，初值为x=0.1，y=0.2,z=0.3,w =0.4，保证了b＞α,β＞α．计算可得基本再生数：

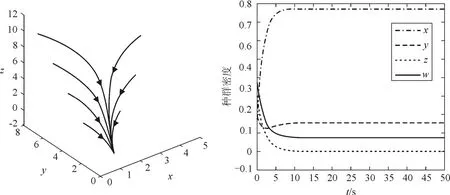
图1 R0＜1时无病平衡点的稳定性Fig 1 Stability of disease-free equilibrium at R0＜1

由定理2可得当R0＜1时，无病平衡点E0是局部渐近稳定的．利用Matlab软件做图，数值模拟系统（5）无病平衡点E0的稳定性，如图1所示．图中横轴t表示时间，纵轴表示数量．由图1可以看出，疾病在无病平衡点E0是吸引的，且最终系统（5）的x,y,z,w等量均趋于稳定状态，疾病感染者人数最终趋于零，即疾病将消亡．

另选取参数b=0.3,β=0.6,ξ=0.01,k =0.2,α=0.01,γ=0.004,p=0.01，初值为x=0.1,y=0.2,z=0.3,w =0.4，保证b＞α,β＞α．计算可得基本再生数：

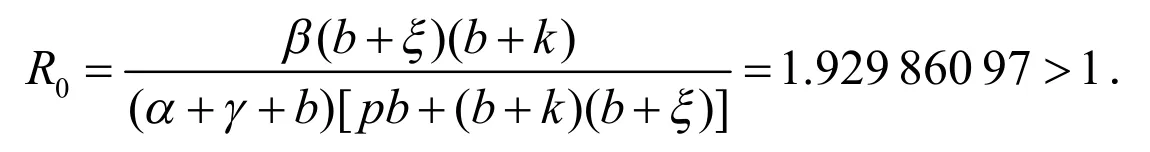
此时系统除无病平衡点外还存在正平衡点E+，由定理3可得当R0＞1时，此正平衡点在Ω0内是局部渐近稳定的．利用Matlab软件做图，数值模拟系统（5）正平衡点E+的稳定性，如图2所示．

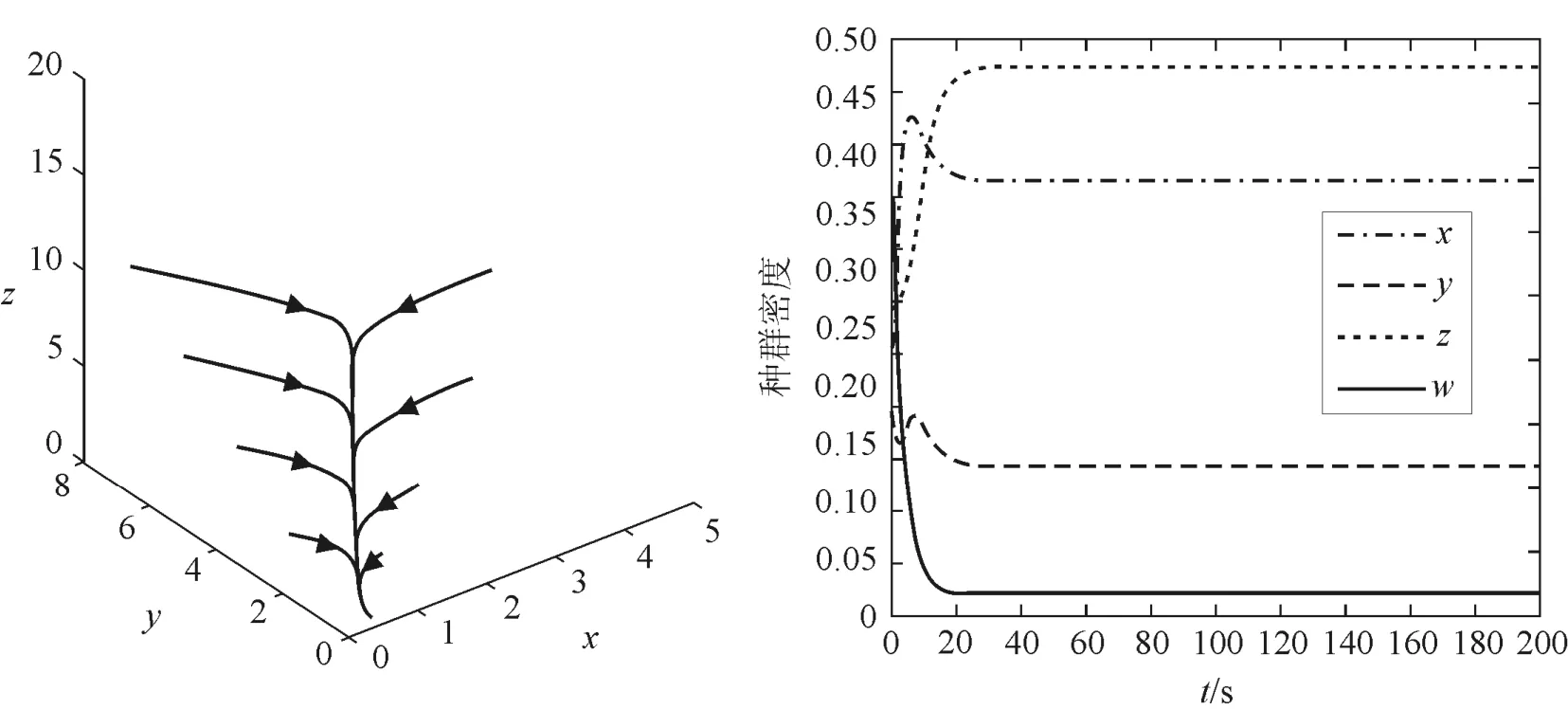
图2 R0＞1时地方病平衡点的稳定性Fig 2 Stability of endemic disease equilibrium at R0＞1

由图2可以看出，疾病在正平衡点E+是吸引的，且最终系统（5）的x,y,z,w等量均趋于稳定状态，疾病感染者人数最终稳定在一个较大且不变的常量，即疾病最终成为地方病．

数值模拟结果表明：当R0＜1时，无病平衡点是全局渐近稳定的；当R0＞1时，地方病平衡点是全局渐近稳定的．但是，模型平衡点的相关全局性分析结果还需进一步理论证明．

4 结 语

本文建立了一类具有阶段结构和免疫逃避并对幼年群体进行连续预防接种的HBV传染病模型，由基本再生数，以及定理2和定理3可以得出，预防接种的比例p越大，基本再生数R0就越小，疾病消亡的可能性就越大，当R0＜1时疾病消亡；一旦患者增多使得接触率β增大导致阈值R0＞1，就会导致疾病成为地方病．与此同时，免疫失去率ξ越大，则基本再生数R0随之增大，则疾病越容易演变成地方病．由模型理论分析和数值模拟结果可知，无病平衡点E0和正平衡点E+最终都达到稳定状态．本文的不足之处在于没有理论分析无病平衡点和正平衡点的全局稳定性．当其它参数确定的情况下，可以计算出使疾病消除的最小预防接种率p，以及最大免疫失去率ξ，进而用来指导乙肝防控策略．

参考文献

[1] Kermack W O,Mckendrick A G. Contributions to the mathematical theory of epidemics [J]. Proc Roy Soc A,1927,115(772): 700-721．

[2] 郭金生，齐文风，唐玉玲．一类具有预防接种和垂直传染的SIR传染病模型的定性分析[J]．贵州大学学报，2014，31（1）：11-14．

[3] 赵明．基于SIRS传染病模型的不同控制策略比较[J]．北华大学学报，2015，16（5）：561-566．

[4] 周毅，娄梅枝，娄洁．一类分年龄阶段的流行病模型研究[J]．工程数学学报，2003，20（3）：135-138．

[5] 于宇梅，张秋娟．一类具有阶段结构的SIRS传染病模型的稳定性[J]．大连交通大学学报，2011，32（3）：99-101．

[6] 宫兆刚，杨志峰．一类具有阶段结构的SIS传染病模型的稳定性[J]．衡阳师范学院学报，2009，30（6）：16-19．

[7] 马知恩，周义仓．常微分方程定性与稳定性方法[M]．北京：科学出版社，2001：41-96．

[8] 张瑜，王辉．一类具有年龄结构的传染病模型稳定性分析[J]．哈尔滨商业大学学报，2010，26（3）：318-320.

[9] Li X Z,Zhou L L. Global stability of an SEIR epidemic model with vertical transmission and saturat-ing contact rate [J]. Chaos Soliton Fract,2009,40(2): 874-884.

[10] Ruan S G,Wang W D. Dynamical behavior of an epidemic model with a nonlinear incidence rate [J]. J Diff Equa,2003,188: 135-163.

[11] 王东明，夏壁灿，李子明．计算机代数[M]．北京：清华大学出版社，2007：36-121．

[12] 肖燕妮，周义仓，唐三一．生物数学原理[M]．西安：西安交通大学出版社，2012：61-103．

The Study on Dynamical Model of HBV Infection

LIU Yingying,LUO Yong,HU Yizheng
(School of Mathematics and Information Science,Wenzhou University,Wenzhou,China 325035)

The paper probes into phenomenon of the immune escape after the vaccination of hepatitis B viral (HBV) and this immune escape is different from the age bracket. The SIRS epidemic model with stage structure and continuous vaccination is considered in this paper. In this infectious disease model,the objects are divided into two stage-structures: the infancy stage and the adult stage; the disease with standard incidence ratio in both infancy and adult groups can be transmitted and only the infancy group is considered to take the continuous vaccination,the asymptotic behavior of this model is studied thereafter. The basic reproductive number R0of this model is obtained in the case of continuous vaccination without considering vertical infection. It is respectively through Routh-Hurwitz criterion that the local stability of the disease-free equilibrium point and the positive equilibrium point are proved. Finally,the appropriate parameters are selected for numerical simulation.

Hepatitis B Virus (HBV); Immune Escape; Stage-structure; Routh-Hurwitz Criterion

O175

：A

：1674-3563(2017)02-0033-09

10.3875/j.issn.1674-3563.2017.03.005 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：封毅)

2016-10-09

刘莹莹(1989-)，女，河南叶县人，硕士研究生，研究方向：微分方程与动力系统