柳合龙，张娅莉，程传敏

(1. 信阳师范学院 数学与信息科学学院，河南 信阳 464000；2. 信阳职业技术学院 数学与计算机科学学院，河南 信阳 464000)

0 引言

对艾滋病传染过程的分析多用常微分方程和离散差分方程,但现实世界是充满随机性的,如感染具有随机性,HIV转化为艾滋病也具有随机性,对于理论研究中只考虑理想的确定性状态这一做法已经不能满足实际的需要,因此在HIV的理论研究中加入随机现象是十分必要的.随机微分方程应用范围非常广泛,经过半个多世纪的努力,众多学者在随机微分方程的理论研究与实际应用方面做出了许多有意义的工作,取得了一系列成果[1-9].DALAL, GREENHALGH 和MAO[10-11]等学者对HIV的随机模型进行了研究. 艾滋病自1985年传入中国,就引起了媒体的高度关注,比如宣传艾滋病的病因、早期症状、传播途径、预防措施以及倡导社会关爱等.媒体对预防艾滋病功不可没.本文将对一类受媒体影响的随机HIV模型加以研究.

1 基本模型

将人群分成易感者和感染者,又把易感者分成两类.第一类受媒体影响较大,即此类人群通过媒体获得关于艾滋病的信息量较多,能够积极采取有效措施避免自己被感染.同样,感染者也会采取措施不传染他人.第二类受媒体影响较小,受感染的机会较大.令α1和α2分别表示第一类和第二类易感者没有受媒体影响的概率(0≤α1≤α2≤1),则第一类受媒体影响的程度为1-α1,第二类受媒体影响的程度为1-α2.为简便起见,本文考虑α1=0,即第一类易感者受媒体影响的概率为1.在这种情况下,第一类易感者不参与病毒的传播.变量X1(t),X2(t),X3(t)分别表示第一类易感者、第二类易感者、感染者在t时刻的数量.本文研究随机HIV模型如下:

(1)

(2)

(μ+σ)X3(t))dt-σ1X3(t)dB(t).

(3)

其中：T(t)=X1(t)+X2(t)+X3(t)；λ1,λ2分别为第一、二类易感者的移入率;μ是自然死亡率;β是艾滋病病毒的传染率;c是单位时间内每个个体接触的性伴侣的个数;D21代表第二类易感者受到媒体的影响变成第一类的转移率;σ是感染者发展成为艾滋病患者的概率;σ1>0(比σ小)是噪音强度.令X(t)=(X1(t),X2(t),X3(t))T.定义

引理1[11]对任何的u∈R1,u>0有u≤2(u+1-lnu)-(4-2ln 2).

(4)

下证τ=,a.s. (反证法)假设命题不真,则存在常数T>0和ε∈(0,1)使得P{τ≤T}>ε,因此存在整数k1≥k0,使得对所有k≥k1有

P{τk≤T}≥ε.

(5)

其非负性可以从u+1-lnu≥0,∀u>0得出.

(1-X3(t))σ1dB(t),

X2(t)≤2(X2(t)+1-lnX2(t))-(4-ln 2).

从而

dV(X(t))≤(c1+λ1+λ2+

D21·2V(X(t)))dt+

(1-X3(t))σ1dB(t)≤

(C2(1+V(X(t)))dt+

(1-X3(t))σ1dB(t),

其中C2=max(c1+λ1+λ2,2D21).因此,当t1≤T时有,

EV(X(τk∧t1))≤V(X0)+C2T+

由Gronwall不等式得,

EV(X(τk∧T))≤C3,

(6)

其中C3=(V(X0)+C2T)eC2T.

C3≥E[IΩkV(X(τk,ω))]≥

令k→得>C3=,矛盾.因此τ=,a.s.证毕.

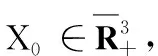
证明考虑如下两种情形:

(i)X3(0)=0,X1(0)≥0,X2(0)≥0.

若X3(0)=0,则X3(t)=0,∀t,a.s.由式(2)得

因此,对任意的t都有X2(t)>0,a.s.

(ii)X3(0)>0,X1(0)≥0,X2(0)≥0.

不失一般性,设X1(0)>0,X2(0)>0,把时间原点变为△t,其中△t为很小的正数,则根据定理1得Xi(t)>0,1≤i≤3.证毕.

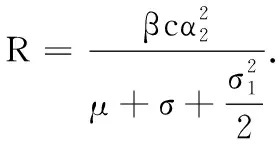
证明由方程(2)得

积分得

从而

(7)

由方程(1)得

从而

(8)

对X3(t)分两种情况讨论:

(i)X3(0)>0.

(9)

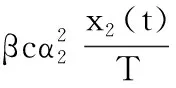
X3(t)≤Me-vt,∀t≥0,a.s.

(10)

(ii)X3(0)=0.

当X3(0)=0时,X3(t)=0,∀t,a.s.所以当X3(0)≥0时式(10)成立,即0≤X3(t)≤Me-vt.因此

(11)

由式(10)得

(12)

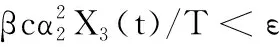
(13)

综合式(7)和式(13)得

(14)

根据极限的定义,对任取ε>0,存在G>0,当t>G时有

(15)

由方程(1)知,当t>G时,

由ε的任意性得

(16)

同理,由不等式(15)的左半部分得

(17)

综合不等式(16)和(17)得

(18)

综合式(11)、(14)和(18)可知,当t→时,证毕.

定理4 当R<1时,无病平衡态是几乎必然局部指数稳定的;当R>1时,无病平衡态是几乎必然指数不稳定的.

证明先讨论X3(t).在人口无病平衡态邻近,由式(1)得

|X3(t)|≤|X3(0)|Ce-λte-σ1B(t),

因此存在t0,当t≥t0时有X3(t)|≤|X3(t0)|e-λ(t-t0),a.s.

从而

|ξ(t)|≤|ξ(t0)|e-(μ+D21)(t-t0)+

Ne-λ(t-t0),a.s.,

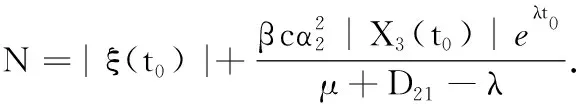
最后讨论X1(t).令

则

所以

|η(t)|≤|η(t0)|e-μ(t-t0)+

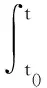
因此当t≥t0时有,

C1e-λ(t-t0),a.s.

若R>1,不妨取X3(0)=1,则

X3(t)=exp(-mt-σ1B(t)).

2 数值模拟

本节将对系统(1)-(3)中的参数选取合理的数值进行模拟,从图像中观察X1,X2和X3的变化趋势.

取β=0.1,σ=0.3798,c=5,α2=0.8,μ=0.015,σ1=0.2,λ1=10,λ2=15,D21=0.05,则R=0.7715<1.初值取X1(0)=400,X2(0)=400,X3(0)=30,Δt=0.002.根据Milstein的一阶差分近似方法[12],利用Matlab软件可以得到X1,X2和X3关于时间的图像(限于篇幅这里仅给出X3的时间序列图，见图1).从图1可以看出，感染者的数量随着时间的推移在t=15附近趋于0,即感染者随着时间的发展最终消亡了.

数值模拟的结果显然与定理3证明的结果相吻合.第一类易感者随着时间的推移是增加的,而第二类易感者的数量随着时间的推移是减少的.如前文所述,第一类易感者是受媒体影响较大的一类,第二类易感者是受媒体报道影响较小的一类,注意到在建模过程中考虑到了第二类易感者受媒体影响而成为第一类易感者的转移率D21.一个增加一个减少可能正是媒体在艾滋病传播过程中发挥积极的作用,而且HIV感染者最终消亡了也正是我们所期望的.

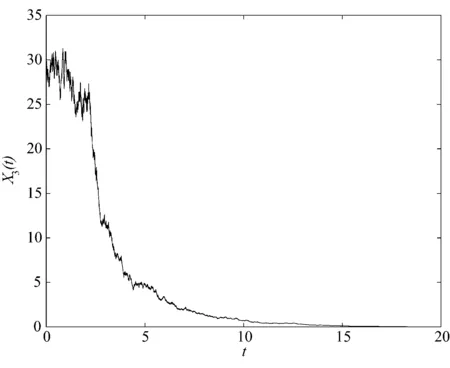
图1 感染者随时间变化图像

3 结束语

本文研究了一类受媒体影响的艾滋病随机模型.通过研究发现,在一定条件下,感染者最终消亡.在建模过程中将艾滋病病毒的传染率定为一个常数β,事实上,艾滋病病毒的传染率跟感染者所处的时期有关,因此研究带有年龄结构的随机微分方程更有意义.