林冰生，衡太骅

（1. 华南理工大学 数学学院，广东 广州 510641；2. 安徽大学 物理与材料科学学院，安徽 合肥 230601）

利用Mathematica计算算符的编序和对易关系

林冰生1，衡太骅2

（1. 华南理工大学 数学学院，广东 广州 510641；2. 安徽大学 物理与材料科学学院，安徽 合肥 230601）

借助Mathematica软件以及形变量子化中的Moyal星乘积的数学性质，实现了用计算机来计算量子力学中一些常见的算符的编序以及对易子的方法．这个方法可以用来快速计算量子力学中常用的一些算符的数学关系．

对易关系；算符编序；Mathematica；Moyal星乘积

1 引言及预备知识

在量子力学的学习和教学中，所接触到的大部分算符的乘积是非对易的，如位置动量算符和，产生湮灭算符+和-等.因此，经常需要考虑算符之间的编序，即不同算符乘积的排列顺序，如Weyl编序、标准编序和反标准编序等［1］.算符的不同编序对应的计算结果是不同的，有时也需要考虑算符在不同编序下的转换.如在位置表象下，动量算符表示为偏微分算子，因此涉及到位置动量算符的数学表达式，在实际计算时一般都会把动量算符放在右边，这实际上就是标准编序的形式.在计算产生湮灭算符的函数的期望值时，可以考虑将其展开为反标准编序的形式，这样在真空态中的期望值就是唯一的常数项.

另外，也经常需要计算各种算符之间的对易子，如计算某些可观测量的不确定度.一般的算法是利用基本算符之间的对易关系以及对易子的运算性质，把原来较为复杂的算符的对易子分解为一系列相对简单的对易子来计算.对于简单的算符，它们之间的对易子是比较容易计算的，或者有现成的公式可以化简.而对于结构稍微复杂的算符，这个计算量通常还是比较大的.

Mathematica等数学软件的优点正是可以代替人类做这种大量的简单重复性运算.利用Mathematica计算常见函数的求导积分或者矩阵运算是我们比较熟悉的，而对于量子力学中常见的非对易算符的相关数学计算，在Mathematica并没有直接的函数可以利用.本文结合Moyal星乘积的性质，实现用Mathematica计算量子力学中常见的算符的编序和对易关系.

Moyal星乘积也称为Weyl-Groenewold乘积，最初是20世纪40年代Groenewold［2］和Moyal［3］等人在研究量子力学基础理论时得到的，近年来被广泛应用于形变量子化和非对易空间等领域的研究［4-6］.如考虑最简单的二维相空间，记坐标为x，动量为p，则函数f和g之间的Moyal星乘积（以下简称为星乘积）可以定义为［7］

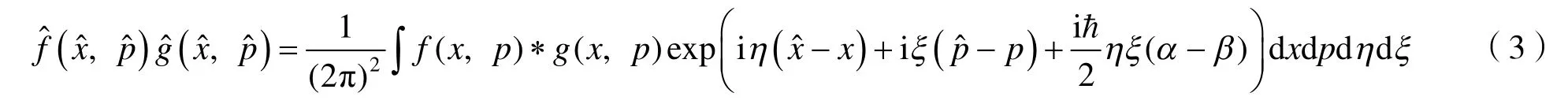
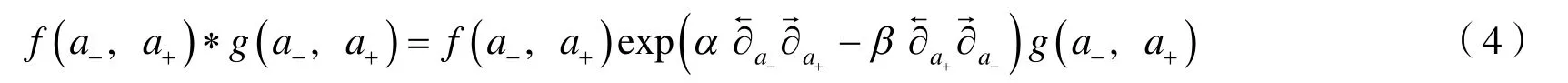
2 利用Mathematica计算算符的编序和对易关系

本文利用Mathematica数学软件进行一些函数的星乘积计算，从而得到相应的算符的编序和对易子.采用关于偏导算子的指数函数的泰勒展开式，当然实际计算中很多时候只需要保留有限项就可以计算出精确的结果.虽然理论上Weyl编序是最为对称的表达形式，但是实际计算时，总是把算符和各自集中写在一起，把算符+和-各自合并一下，最终结果一般不会写成完全对称的形式.当然不同的表达形式在考虑正则对易关系之后，其取值是相同的.所以将把最终的结果用标准编序或者反标准编序的形式写出来.

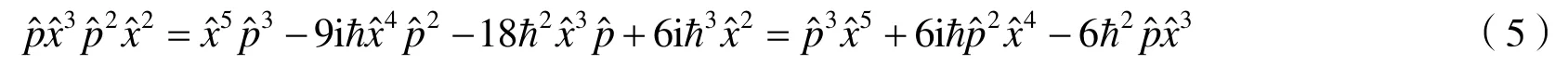
在定义星乘积的求和式中，根据具体的函数次数，可以调整求导的次数，这里上限都是取20次，当然实际计算用不了这么多.在最后的输出形式中，因为Mathematica里面的输出结果是按照字母排序的，并不对应具体的算符顺序，所以在写成算符表达式时需要手动调整一下.如Out［3］给出的是标准编序的结果，所以在算符表达式中默认在左边在右边；Out［4］给出的是反标准编序的结果，所以在算符表达式中默认在左边在右边.可以看到，Mathematica给出的结果和手算的结果（5）是完全一致的.当然对于更复杂的更高次幂的算符，用Mathematica计算要方便很多，其计算速度和准确度也不是手算可以比拟的.

显然上述计算结果通过手算是不容易得到的.利用类似的表达式，也可以计算关于算符和的函数的对易子.星乘积在高维相空间中也有类似的表达式，所以计算方法可以很容易地推广到高维的情形.

3 结论

本文利用Mathematica数学软件和形变量子化中Moyal星乘积的数学性质，实现了用计算机计算简单的算符编序以及算符之间的对易子.从本文的例子可以看到，利用Mathematica实现这些计算相比手工计算在速度和准确度上都有极大的提高.本文方法可以帮助学生和研究人员在学习和研究量子力学相关问题时利用计算机辅助来提高计算效率，并且对于Moyal星乘积和形变量子化的学习也有利于学生更深入地理解经典力学和量子力学的过渡以及量子力学的本质.

本文方法基本上只是对于算符的对易子为常数的情况适用，对于对易子仍然为算符的情况就不适用了.另外，因为采取的是偏导算子的指数函数的泰勒展开式，只保留其前面的有限项，因此对于复杂的函数只能得到有限项展开的近似结果，如算符的指数函数.当然对于指数函数形式的对易关系，很多时候是可以使用现成的数学公式来化简的［8］.事实上，这里也可以考虑使用星乘积的积分表达式，但是积分形式在Mathematica等数学软件里面表现不太理想，主要是积分的收敛性容易判断错误，这些问题有待进一步的研究解决.

目前已经有专门计算非交换代数相关数学公式的Mathematica软件包，如NCAlgebra［9］.但开发这个软件包更多的是为纯数学上的非交换代数相关计算推导服务的，并且这个软件包里面定义的函数比较多，物理专业的学生要熟练掌握是不容易的.而对于本文讨论的这类常见于量子力学中的计算，显然本文的计算方法更简单实用，尤其对于计算与算符编序相关的问题，使用Moyal星乘积的优势更为明显.

［1］ 范洪义，楼森岳，张鹏飞.量子力学坐标-动量算符幂次排序互换的简捷公式与新推导方法［J］.物理学报，2015，64：160302

［2］ Groenewold H J.On the principles of elementary quantum mechanics［J］.Physica，1946，12：405-460

［3］ Moyal J E，Bartlett M S.Quantum mechanics as a statistical theory［J］.Mathematical Proceedings of the Cambridge Philosophical Society，1949，45：99-124

［4］ Zachos C.Deformation quantization：quantum mechanics lives and works in phase-space［J］.Int J Mod Phys A，2002，17：297-316

［5］ Seiberg N，Witten E.String theory and noncommutative geometry［J］.J High Energy Phys，1999（9）：32

［6］ Kupriyanov V G.Dirac equation on coordinate dependent noncommutative space-time［J］.Phys Lett B，2014（732）：385-390

［7］ Hirshfeld A C，Henselder P.Deformation quantization in the teaching of quantum mechanics ［J］.Am J Phys，2002（70）： 537-547

［8］ 喀兴林.不对易算符的代数运算［J］.大学物理，1992，11（1）：6-10

［9］ Helton B，Miller R L，Stankus M，et al.NCAlgebra ［EB/OL］.（2015-10-10）［2016-03-22］.http：//www.math.ucsd.edu/～ncalg/

Using Mathematica to calculate the orderings and commutation relations of operators

LIN Bing-sheng1，HENG Tai-hua2
（1. School of Mathematics，South China University of Technology，Guangzhou 510641，China；2. School of Physics and Material Science，Anhui University，Hefei 230601，China）

By virtue of Mathematica software and the mathematical properties of Moyal star product in deformation quantization， a method of using the computers to calculate the orderings and commutators of some common operators in quantum mechanics is implemented.This method can be used to quickly calculate the mathematical relations of some common operators in quantum mechanics.

commutation relation；operator ordering；Mathemtica；Moyal star product

O411.1

A

10.3969/j.issn.1007-9831.2016.06.005

1007-9831（2016）06-0017-04

2016-03-10

国家自然科学基金资助项目（11405060，11571119）

林冰生（1982-），男，广东揭阳人，讲师，博士，从事数学物理研究.E-mail：sclbs@scut.edu.cn