☉江苏省南京市溧水区第二高级中学 王敬全

换元法求解函数问题例说

☉江苏省南京市溧水区第二高级中学 王敬全

函数问题是近几年高考的重点和热点，也是学生学习的难点，对于一类值域问题，使用换元法解决是一种常见方法，下面笔者结合平时的教学实践谈谈换元法解决函数问题.

一、巧用换元法求解函数最值问题

在函数的一类求最值问题中，常常可以配凑成平方和的形式，此时可以利用同角的三角函数进行三角换元，达到减少未知量的目的.

例1若实数x，y满足x2+y2+xy=1，则x+y的最大值是______.

三角换元法是一种常见的数学方法，利用它可将代数问题化为三角问题，然后利用三角函数的性质简单解决.

二、巧用换元法求无理函数的值域

对无理函数的值域求法通常有判别式法、三角换元法、构造平面向量法、构造截距法、构造点到直线的距离法等.但最直接的思想就是将无理函数的值域问题转化为有理函数的值域问题.即通过变量换元法将无理函数的值域问题转化为有理函数的值域问题，思路新颖别致.

1.巧引斜率进行换元

（1）如果三项式ax2+bx+c有相异实根λ，μ，即ax2+bx+ c=a（x-λ）（x-μ），则可令.其几何意义是：如果三项式ax2+bx+c有相异实根λ，μ，则二次曲线y=与x轴交于两点（λ，0），（μ，0）.过其中一点例如（λ，0）的割线为y=t（x-λ）.对于斜率t取定值，二次曲线与它的割线有另一个交点.显然，当t在某一范围内连续变动时，这些交点（x，y）描出二次曲线y=为借助参数t表示坐标x，将两边平方得到t2（x-λ）2=ax2+bx+c，但点（λ，0）在二次曲线上，因而aλ2+bλ+c=0.故t2（x-λ）2=a（x-λ）（x+λ）+b（x-λ），两边约去非零因式x-λ，得t2（x-λ）=a（x+λ）+b，这是关于x的一次方程，因而x可表示为t的有理函数，进而所求函数就可以表示为t的有理函数，而这正是我们所期望实现的.显然，令也可同样达到目的.

点评：如果本题用判别式法做，将等式两边平方时会将字母的取值范围放大，且利用Δ≥0是在x属于全体实数时求解的，若不注意x满足的其他一些条件非常容易出错.

2.巧引截距作为变量进行变量换元

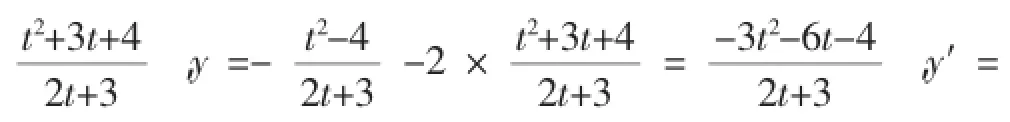
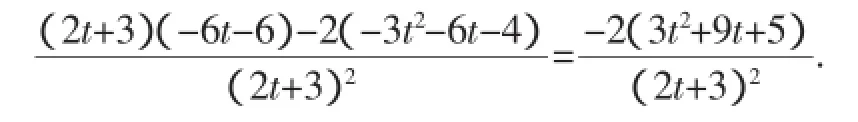
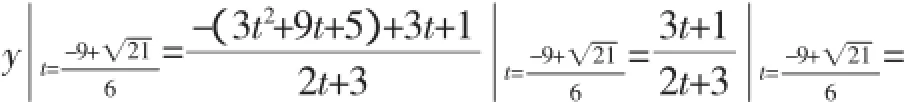
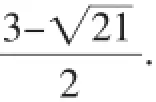
换元法的本质是用一种变量形式去取代另一种变量形式，从而把繁杂的无理函数问题转变为简单的有理函数问题，新变量的范围由新变量的几何意义决定.

三、利用换元法揭示函数周期

在中学数学中，有些数学问题，表面上看与周期毫无关系，但实际上隐含着周期性，一旦揭示了周期，问题便迎刃而解了.在解题中，我们常用换元法揭示函数的周期.

例4已知f（x）为R上的偶函数，g（x）为R上的奇函数且g（-1）=3，g（x）=f（x-1），则f（2012）+g（2013）= _______.

解析：由g（x）=f（x-1），得f（x）=g（x+1），f（-x）=g（-x+ 1），因为f（x）为R上的偶函数，所以g（1+x）=g（1-x），g（x）的图像关于x=1对称，g（-x）=g（x+2）.又因为g（x）为R上的奇函数，所以g（x）=-g（-x）=-g（x+2），用x+2代替x得g（x+2）=-g（x+4），故g（x）=g（x+4），得g（x）是周期为4的周期函数.所以f（2012）+g（2013）=2g（2013）=2g（503×4+1）= 2g（1）=-6.

点评：由此题我们可以得知：（1）设f（x）是R上的偶函数，且图像关于直线x=a（a≠0）对称，则f（x）是周期函数，且2|a|是它的一个周期.（2）设f（x）是R上的奇函数，且图像关于直线x=a（a≠0）对称，则f（x）是周期函数，且4|a|是它的一个周期.对于以上两个常用结论，可以概括为：对称性+奇偶性=周期性.

四、换元法解决一类复合函数问题

形如y=f［f（x）］的复合函数相关问题，在近几年的高考中屡见不鲜，常以压轴选择题或填空题的形式考查，相关资料对该类问题的解答通常为分类讨论，过程繁杂且不易于学生接受，更谈不上举一反三、触类旁通了.从复合函数角度出发，利用换元思想，可以快速简便求解此类题目.

通过换元，借助函数y=f（t）和y=2t的图像可解决问题1（图1）.

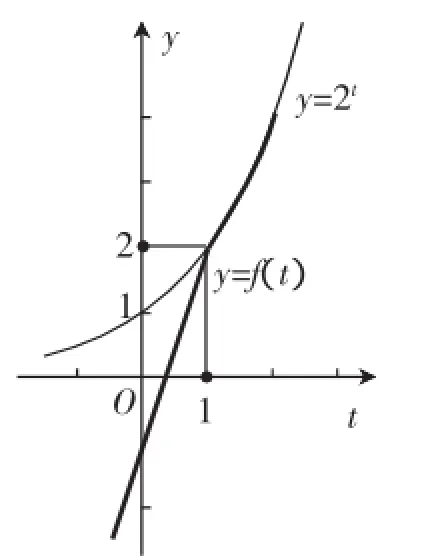
图1

图2

由图1知，满足f（t）=2t的t的取值范围是t≥1，而t的取值范围与a的取值范围又有关联，即f（a）≥1.借助函数t= f（a）的图像解决问题2（图2）.

总结：我们可归纳出解决该类问题的一般性方法：

（1）先进行换元，将复合函数y=f［f（x）］利用换元思想写成两个函数y=f（t）和t=f（x）.

（2）分别在直角坐标系tOy和直角坐标系xOt中画出函数y=f（t）和t=f（x）的图像.这里需要说明的是，一般情况下，两幅函数图像应该不一致，只有当自变量t与自变量x的取值范围相同时，图像保持一致.

（3）在直角坐标系tOy中，借助函数y=f（t）的图像求出t的范围（问题1），再在直角坐标系xOt中，利用函数t= f（x）的图像求出x的范围（问题2）.

以上解法很好地回避了分类讨论过程，将整个解题过程以图形方式直观地呈现出来，易于学生理解与接受，同时注重了函数教学中需强化的数形结合思想.

换元法不仅是数学中的重要思想方法，而且还是解题中不可或缺的工具.它能够使某些复杂的数学问题简单化，从而提高了做题效率，减少了出错率.在解题中换元法和换元思想是数学常规解题思路中比较重要的，在解答某些数学问题时运用此思想可以收到意想不到的效果，同时可以发散解题者的数学思维，使数学思想得到凝练.F