☉浙江省杭州市余杭实验中学 王国军

解析几何解题训练中的几点注意

☉浙江省杭州市余杭实验中学 王国军

解析几何是高中数学主干内容之一，在历年各省市的高考命题中常以中、高档题型出现，处理此类问题的常用策略主要有：（1）几何问题直接代数化；（2）先把几何问题利用几何方法进行适当处理后，再代数化.学生在解题中常因为对平面几何的几何特征把握不准，造成解题过程过于烦琐，使解题半途而废.本文对此提出以下几种建议，供参考.

一、注意积累几何特征代数化的经验

在对解析几何问题的分析中不难发现隐藏于其中的平面几何身影，准确利用平面几何的几何性质是问题顺利求解的关键.其中涉及较多的平面几何中的图形有平行四边形、菱形、等腰三角形等.

图1

（1）当B是W的右顶点且四边形OABC为菱形时，求此菱形的面积.

（2）当B不是W的顶点时，判断四边形OABC是否可能为菱形，并说明理由.

解析：菱形的几何性质综合起来主要有以下几点：

①对边平行；②对边相等；③对角线平分；④对角线垂直；⑤对角线中点重合；⑥对角线平分其面积；⑦菱形面积|等.

解题中只要准确把握上述几何特征，即可准确将几何问题代数化.如第（2）问判断四边形OABC是否可能为菱形，可从菱形的几何特征入手：先假设对角线互相平分，再判断对角线是否垂直.

如果题目中涉及的是平行四边形，菱形这个条件可

以弱化为平行四边形，结论①、②、③、⑤、⑥不变.若将点C去掉，将菱形这个条件改为△ABO为等腰直角三角形呢？（请读者思考）

二、注意从多角度分析，预测多种途径的繁简，以优化解题思路

图2

对于同一道问题，可能有多种处理方式，有的烦，有的简，因此，在解题训练中要善于从不同角度分析、解决问题，并从中选择最优策略.

例2如图2，设AB、A′B′分别是圆O：x2+y2=a2和椭圆C的弦，端点A与A′、B与B′的横坐标分别相等，纵坐标分别同号.

（2）方法1：先入为主、直奔主题.

由（1）得圆O的方程为x2+y2=4.

设A（x1，y1）、B（x2，y2）、A（′x1，m）、B（′x2，n）.因为点A在圆O上，所以+=4①.

（x-x1），即y

直线A′B′的方程为y

该解法从题意出发，设出关键点的坐标，再结合共线原理，找到定点，思路简洁、易入手.但对学生的运算求解能力、推理论证能力提出了更高的要求.

方法2：先猜后证，峰回路转.

由（1）得圆O的方程为x2+y2=4.

设A（x1，y1）、B（x2，y）2.

又kA′M′=结合①式，得kA′M′=kB′M′，所以A′、M′、B′三点共线，即弦A′B′必过定点M

此解法充分利用圆与椭圆之间的关系，即圆经过压缩可转化为椭圆、椭圆通过相反的变化过程可转化为圆，大大简化了计算.在探究弦A′B′是否也必过某个定点时，巧妙利用“先猜后证”的策略，降低了问题求解的难度.

三、注意综合运用合情推理与演绎推理、综合法与分析法探索问题解决思路

解析几何问题具有较强的综合性，着重考查直线与椭圆的位置关系、椭圆的定义、弦长公式、平行线的性质、勾股定理、三角形面积等知识，能有效考查考生分类与整合的思想综合运用能力，以及运算求解能力和推理论证能力.

别为（-2，0），（1，0）.过R作不平行于x轴的直线交椭圆于A，C，直线AP交椭圆于B，连接BR交椭圆于D.证明直线AB与直线CD的斜率之比为定值，并求出该值.

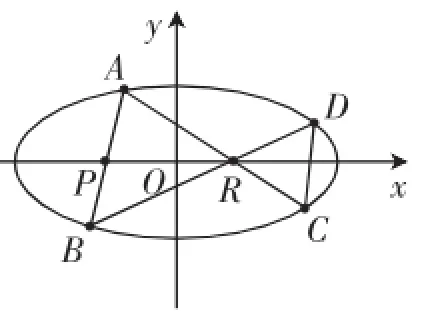
图3

解析：题中所涉及的点均在椭圆上.因此可设变量直接将所有点的坐标表示出来，再进行计算化简.

设直线AC：y=k（x-1），A（x0，kx0-k）.将直线AC：y= k（x-1）代入椭圆方程得（1+5k2）x2-10k2x+5k2-5=0，由根与系数的关系可知xC=将AP：y=（x+2）代入椭圆方程得x2+，再代入直线方程求出yB，类似地，求出点D坐标，再由斜率公式代入化简求比值.

这种方法思维直接，容易操作，但对运算的准确性要求高，需要有扎实的基本功.真正能解出来的同学寥寥无几.

若仔细挖掘隐含条件，不难发现题中4个点都是由两条过点R的直线与椭圆相交产生，对称性不言自明.故设直线BD和AC的方程，得如下简洁解法.

设直线BD：x=m1y+1；直线AC：x=m2y+1.

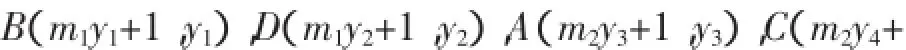
将x=m1y+1代入，则.同理

无疑，通过此类问题的求解训练，可以有效地检测和提高学生分析问题、解决问题的能力.

四、注意数形结合、函数与方程、化归转化思想在解决问题中的作用

数形结合思想、函数方程思想、转化与化归思想是高中数学常规数学思想，渗透于高中数学各知识模块中，解析几何也不例外.

例4如图4，已知抛物线C：y2= 8x的焦点为F，准线为l，P是l上一点，Q是直线PF与C的一个交点，若，则|QF|=（）.

C.3D.2

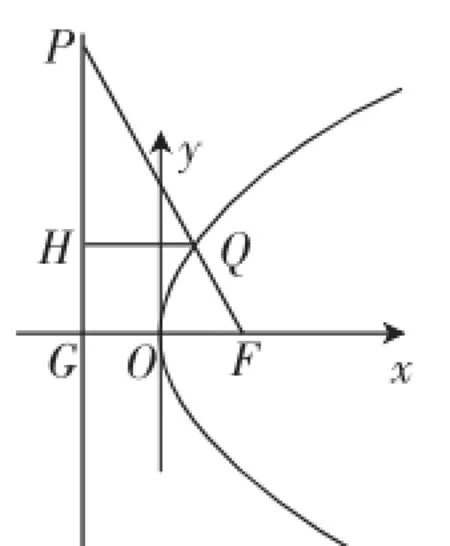
图4

解法1：（代数法）F（2，0），P（-2，a），Q（x，y），得到x=1，代入抛物线方程得到，|QF|=3.

解法2：（几何法）过Q点向准线l作垂线，垂足为H，设|QF|的长度为x，由抛物线的定义，|QH|=|QF|=x，由，得到，所以x=3.

数形结合就是把代数上的“数”与几何上的“形”，结合起来认识问题、理解问题的思想，它包括两个层面，即以“形”助数，和以“数”解形.解题中要灵活应用.

总之，我们在处理解析几何问题时既要从“大处着眼”，即在整体上把握问题的综合信息和处理问题的策略，又要从“小处着手”，即在细节上能熟练运用各种数学方法与技巧.注意掌握一些优化解析运算的策略，进而提高我们分析问题与解决问题的能力.F