ERV族分布下带投资的双险种风险模型的破产概率

2016-10-17王施施王文胜骆明旭

杭州师范大学学报(自然科学版) 2016年5期

关键词：险种正态分布对数

王施施, 王文胜, 骆明旭

(杭州师范大学理学院,浙江杭州 310036)

ERV族分布下带投资的双险种风险模型的破产概率

王施施, 王文胜, 骆明旭

(杭州师范大学理学院,浙江杭州 310036)

破产概率；双险种风险模型；渐近关系式；风险投资策略

1　引言和模型

在实际生活中,保险公司业务种类日益增多,在索赔方面要考虑的因素也越来越复杂,因此经典风险模型中单一险种的情形已不能满足实际需要.为了更好地描述这些不确定因素,本文引入了带投资的双险种风险模型,利用此模型对破产概率进行深入研究.

我们假定保险公司拿出一部分盈余投资Black-Scholes型资本市场指数,且假设该指数的价格过程由几何布朗运动来表示,那么公司的盈余过程{Ui(t),t≥0}可表示为:

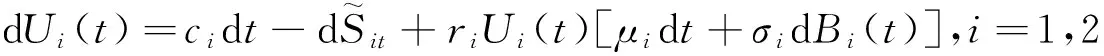
(1)

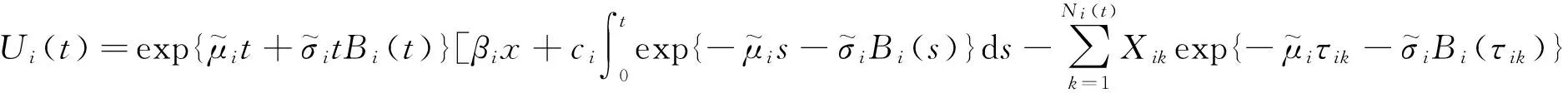
(2)

其中{Ni(t),t≥0,i=1,2}是第i险种到时刻t为止保单发生索赔次数.假设它服从参数为λit的泊松分布,且{N1(t),t≥0},{N2(t),t≥0}相互独立,而且{Xik,k=1,2,…,i=1,2},{Bi(t),i=1,2,t≥0},{Ni(t),i=1,2,t≥0}都是相互独立的.

在有限时间T(T>0),关于双险种情形的破产时刻及破产概率有多种定义.本文主要研究其中的3种,它们具体定义为:

1)定义破产时刻Tmax(x)为:

Tmax(x)=inf{t≥0:max{U1(t),U2(t)}<0|U1(0)=β1x,U2(0)=β2x},

相应的破产概率为:

Ψmax(x,T)=P(Tmax(x)≤T)

(3)

2)定义破产时刻Tmin(x)为:

Tmin(x)=inf{t≥0:min{U1(t),U2(t)}<0|U1(0)=β1x,U2(0)=β2x},

相应的破产概率为:

Ψmin(x,T)=P(Tmin(x)≤T)

(4)

3)定义破产时刻Tsum(x)为:

Tsum(x)=inf{t≥0:U1(t)+U2(t)}<0|U1(0)=β1x,U2(0)=β2x},

相应的破产概率为:

Ψsum(x,T)=P(Tsum(x)≤T)

(5)

在保险精算的应用中破产概率的研究一直是热门的话题.迄今,国内外很多学者研究过连续或者离散时间风险模型的破产概率.例如,Asmussen和H∅jgaard[1],Cossette[2],Chen[3]等.然而,这些都是对单一情形的研究,难免和实际不相符合.后来,二维风险模型逐渐被广大学者探讨和研究出来,如Avram[4],Li[5],Dang[6],Zhang和Wang[7].

本文主要集中研究带投资的双险种风险模型的破产概率,给出了破产概率主要结果和其他一些概率以及相应的证明以及证明所需要的引理.

2　定义和主要结果

2.1相关概念

定义1对任意固定的实数α>0,如果分布F满足

(6)

则称F属于R-α族.通常,R族是指所有R-α族关于α在其取值范围上的并集.

定义2对任意固定的实数0<α≤β<∞,如果分布F满足

(7)

则称F属于ERV-α,-β族.通常,ERV族指所有ERV{-α,-β}族关于α≤β在其取值范围上的并集.

对于更新风险模型(2),全文假设索赔额分布Fi∈ERV(-α,-β),1<α≤β<∞,且

(8)

假设该条件保证了公司盈余的随机波动能被趋势控制,否则公司将以概率1破产.详见文献[8-9].

从现在开始除非特别指明,所有极限过程均指x→∞时情况,对于两个正函数f(·)和g(·),如果limf(x)/g(x)=1，记为f(x)～g(x);如果liminff(x)/g(x)≥1,记为f(x)g(x);如果limsupf(x)/g(x)≤1,记为f(x)g(x);如果limsupf(x)/g(x)<∞,记为f(x)=○(g(x)).

2.2主要结果

定理1考虑更新风险模型(2),令LN(yi;a,b2)表示参数为a和b2的对数正态分布,如果索赔额{Xik,k=1,2,…,i=1,2}是独立同分布且非负的随机变量,其分布Fi∈ERV(-α,-β),1<α≤β<∞,且式(8)成立.则式(3)定义的破产概率具有如下渐近关系式:

(9)

定理2考虑更新风险模型(2),令LN(yi;a,b2)表示参数为a和b2的对数正态分布,如果索赔额{Xik,k=1,2,…,i=1,2}是独立同分布且非负的随机变量,其分布Fi∈ERV(-α,-β),1<α≤β<∞,且式(8)成立.则式(4)定义的破产概率具有如下渐近关系式:

(10)

定理3考虑更新风险模型(2),令LN(yi;a,b2)表示参数为a和b2的对数正态分布,如果索赔额{Xik,k=1,2,…,i=1,2}是独立同分布且非负的随机变量,其分布Fi∈ERV(-α,-β),1<α≤β<∞,且式(8)成立.则式(5)定义的破产概率具有如下渐近关系式:

(11)

3　定理的证明

3.1引理

引理1考虑单一险种情形下,具有共同分布F的独立索赔额序列{Xk,k=1,2,…},如果F∈ERV(-α,-β),1<α≤β<∞,则

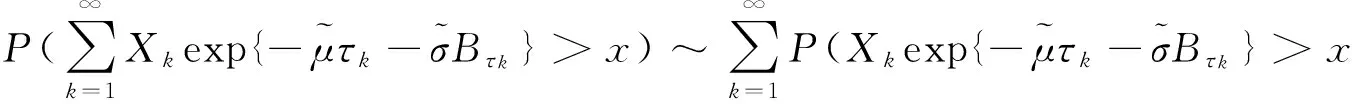
(12)

引理2设X和Y是两个相互独立的非负随机变量,X的分布F∈ERV(-α,-β),1<α≤β<∞,且存在0<δ<α,使得EYβ+δ<∞,则存在常数D>0,使得

(13)

证明参见文献[11]中定理3.5.

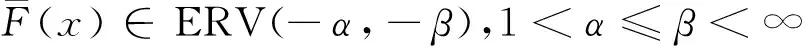
(14)

证明参见文献[11].

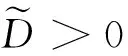
(15)

证明参见文献[12]中引理3.1.

引理5对于单一险种情形下带投资的风险模型,

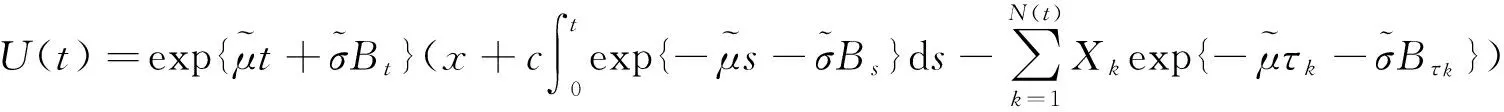
其中LN(y;a,b2)表示参数为a和b2的对数正态分布,如果索赔额分布F∈ERV(-α,-β),1<α≤β<∞,且式(8)成立,则

(16)

证明在假设条件(8)下,由引理1式(12)得

引理6对于单一险种情形下带投资的风险模型,

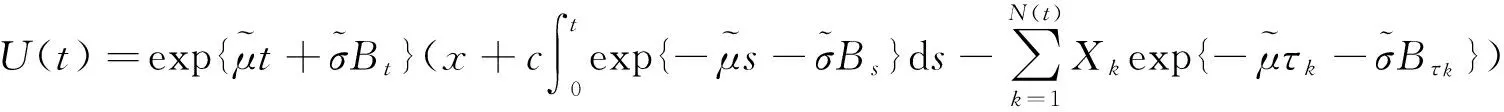
其中LN(y;a,b2)表示参数为a和b2的对数正态分布,如果索赔额分布F∈ERV(-α,-β),1<α≤β<∞,且式(8)成立,则

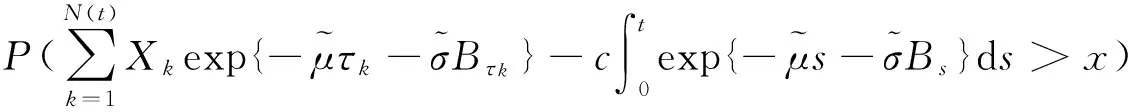
(17)

证明对∀ε>0,

I1(x)-I2(x).

(18)

(19)

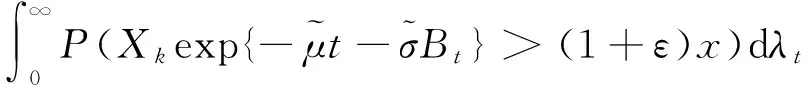
(20)

选取适当的ρ>0,使得β′(1-ρ)>β.根据定义2式(7)有

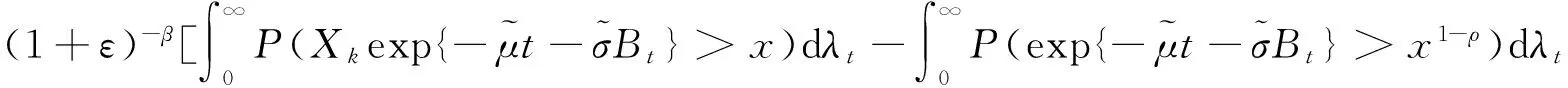
(21)

根据引理2,存在0<δ<α,和常数D>0,使得

(22)

易证式(22)中的积分是有限常数.对于前面定义的β′,有β′(1-ρ)>β,在式(8)条件下,有

(23)

由式(22)、(23)和引理4的式(15)得

综上所述

(24)

进一步,由式(19)(22)和引理4的式(15)得

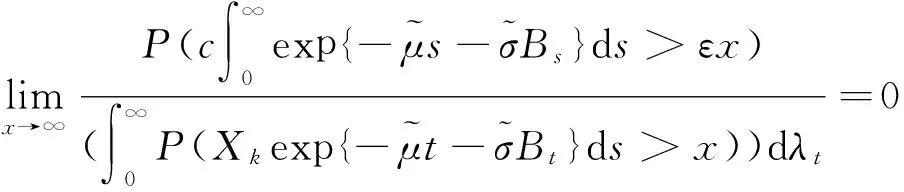
(25)

所以由式(18)(24)(25)和ε>0的任意性得

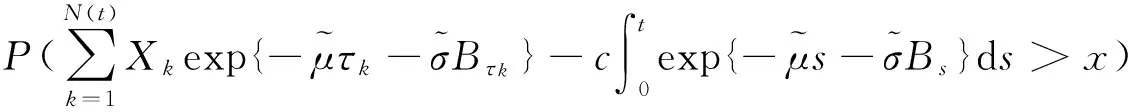
3.2定理1的证明

首先证明式(3)定义破产概率的上界,由破产概率Ψmax(x,T)的定义及条件{N1(t),t≥0},{N2(t),t≥0}相互独立,以及{Xik,k=1,2,…},(i=1,2)独立可知

Ψmax(x,T)=P(Tmax(x)≤T)=P(Ui(t)<0,i=1,2,∃0≤t≤T)=

由引理5得

Ψmax(x,T)

(26)

接着要证明破产概率的下界,根据其独立性有

Ψmax(x,T)=P(Ui(t)<0,i=1,2,∃0≤t≤T)=

由引理6得

Ψmax(x,T)

(27)

所以结合式(26)和(27)可知

3.3定理2的证明

根据破产概率Ψmin(x,T)的定义及在定理2条件下,令s(xi)=inf{t≥0,Ui(t)<0},则

3.4定理3的证明

和定理1的证明一样,首先考虑式(5)定义破产概率的上界,由定理3的条件得

由引理3得

所以

(28)

下面考虑破产概率的下界.

由式(5)破产概率定义得

由引理3得

所以

Ψsum(x,T).

(29)

由式(28)和式(29)得

[1] ASMUSSEN S, H∅JGAARD B. Approximations for finite horizon ruin probabilities in the renewal model[J]. Scand Actuar J,1999(2):106-119.

[2] COSSETTE H, LANDRIAULT D, MARCEAU E. Ruin probabilities in the discrete time renewal risk model[J]. Insurance Math Econom,2006,38(2):309-323.

[3] CHEN Y, NG K W. The ruin probabilities of the renewal model with constant intrest force and negatively dependent heavy-tailed claims[J]. Insurance Math Econom,2007,40(3):415-423.

[4] AVRAM F, PALMOWSKI Z, PISTORIVS M. A two-dimensional ruin problem on the positive quardrant[J]. Insurance:Mathematics and Economics,2008,42(1):227-234.

[5] LI J H, LIU Z M, TANG Q H. On the ruin probabilities of a bidimensional perturbed risk model[J]. Insurance:Mathematics and Economics,2007,41(1):185-195.

[6] DANG L F, ZHU N, ZHANG H M. Survival probability for a two-dimensional risk model[J]. Insurance:Mathematics and Economics,2009,44(3):491-496.

[7] ZHANG Y Y, WANG W S. Ruin probabilities of a bidimensional risk model with investment[J]. Statist Probab Lett,2012,82(1):130-138.

[8] FROLOVA A, KABANOV Y, PERGAMENSHCHIKOV S. In the insurance business risky investments are dangerous[J]. Finance Stoch,2002,6(2):227-235.

[9] DUFRESNE D. The distribution of a perpetuity, with applications to risk theory and pension funding[J]. Scnd Actuar J,1990(1):39-79.

[10] TANG Q, TSITSIASHVILI G. Finite-and infinite-time ruin probability in the presence of stochastic returns on investments[J]. Adv Appl Probab,2004,36(4):1278-1299.

[11] EMBRECHTS PAUL, KlÜPPELBERG C, MIKOSCH T. Modelling extremal events[J]. Applications of Mathematics,2010,71(2):183-199.

[12] TANG Q, SU C, JIANG T, et al. Large deviations for heavy-tailed random sums in compound renewal model[J]. Statist Probab Lett,2001,52(1):91-100.

[13] GJESSING H K, PAULSEN J. Present value distributions with applications to ruin theory and stochastic equations[J]. Stochastic Process Appl,1997,71(1):123-144.

[14] CLINE D B H, SAMORODNITSKY G. Subexponentiality of the product of independent random variables[J]. Stochastic Process Appl,1994,49(1):75-98.

[15] WANG K Y, WANG Y B, GAO Q W. Uniform asymptotics for the finite-time ruin probability of a dependent risk model with a constant interest rate[J]. Methodol Comput Appl Probab,2013,15(1):109-124.

[16] YANG Y, LEIPUS R, SIAULYS J, et al. Uniform estimates for the finite-time ruin probability in the dependent renewal risk model[J]. J Math Anal Appl,2011,383(1):215-225.

[17] SHEN X M, ZHANG Y. Ruin probabilities of a two-dimensional risk model with dependent risks of heavy tail[J]. Statistics and Probability Letters,2013,83(7):1787-1799.

[18] WEI L. Ruin probability of the renewal model with risky investment and large claims[J]. Sci China SerA,2009,52(7):1539-1545.

Ruin Probability of Two-type-risk Insurance Risk Model under ERV Distribution

WANG Shishi, WANG Wensheng, LUO Mingxu

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)