许英姿， 岳书常， 刘灿昌， 刘　露， 荆　栋

(山东理工大学 交通与车辆工程学院， 山东 淄博 255049)



考虑非局部效应的碳纳米管磁时滞最优化控制

许英姿， 岳书常， 刘灿昌， 刘露， 荆栋

(山东理工大学 交通与车辆工程学院， 山东 淄博 255049)

摘要：提出一种考虑非局部效应梁结构非线性振动的磁时滞最优化控制方法.以衰减率为目标函数，以反馈控制参数范围为约束条件，考虑非局部效应参数的影响，利用最优化方法计算得到衰减率最小的控制参数.通过选取最优的时滞量，提高控制系统的控制效果. 研究了非局部效应参数对控制参数和时滞的影响及其影响规律，并通过设计仿真实例进行了减振控制分析.

关键词：非线性振动；控制；最优化方法；响应；时滞

碳纳米管(CNT)的发现引起科学界的巨大关注[1]. 在过去的几年中，对碳纳米管及其复合结构振动行为的研究成为一个研究的热点[2].纳米结构的非线性来源较多，如大挠度、静电驱动、压膜阻尼、分子间表面作用等因素[3-5]，这些非线性因素对纳米管结构的动力学行为产生重要的影响，因而对碳纳米管非线性系统的动力学行为和振动控制研究已经成为当前的一个重要研究课题.

考虑非局部效应纳米结构的线性和非线性动力学研究取得较快的进展.杨晓东等分析考虑非局部效应的两端简支纳米材料梁的横向非线性振动特性[6].考虑非局部效应的碳纳米管的线性和非线性振动得到深入研究[7-9]. Mehdipour等[10]利用考虑非局部效应的欧拉伯努利梁理论研究了悬臂碳纳米管梁的谐振频率和相应的弯曲模量的关系. 近年来，外部纵向磁场对碳纳米管中波的传播和振动影响的研究已经展开. Wang等[11]研究了纵向磁场洛伦兹力对嵌于弹性基的碳纳米管中波传播的影响规律. Narendar等[12]研究了考虑非局部效应的单壁碳纳米管梁在纵向磁场作用下的波的传播规律. Murmu等[13]研究了纵向磁场对考虑非局部效应的双壁碳纳米管梁对横向振动的影响.

1　碳纳米管谐振梁的非线性振动磁控制分析

基于非局部效应欧拉-伯努利梁理论，在谐波激振力和洛伦兹力作用下，单壁碳纳米管(SWCNT)的弯曲振动方程可以写为[10-14]

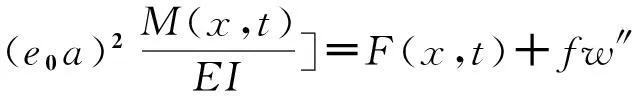
(1)

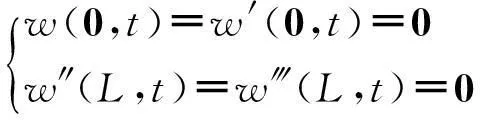
(2)

根据弯曲梁理论，非线性振动方程可以表示为[10-14]

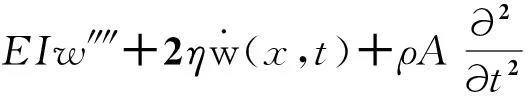
(e0a)2[w″-3a3D2w″3-rw′2w″]}=

EIN(w)+F(x,t)+fw″

(3)

式中，N(w)=3a3D2[2w″(w‴)2+(w″)2w″″]+r[2(w″)3+6w′w″w‴+(w′)2w″″].

将方程(3)表示成无量纲的形式：

(4)

(5)

则边界条件(2)变成

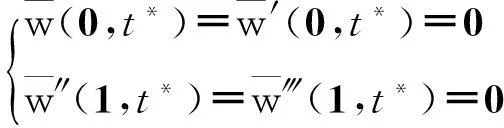
(6)

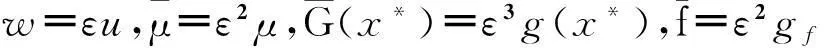
(7)

式中，Nu=2a3(D/L)2[2u″(u‴)2+(u″)2u″″]+r[2(u″)3+6u′u″″u‴+(u′)2u″″]. 将式(7)中的u(x*,t*)和g(x*)分别展开为

(8)

其中φn为悬臂梁的模态函数. 将方程(8)代入方程(7)，得到

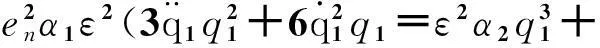
(9)

α2=3a3(D/L)2β21+rβ22;

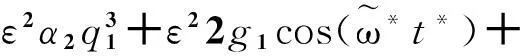
ε22gf1q1(t*-τ)

(10)

(11)

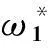
q1(t*,ε)=q10(T0,T1)+ε2q11(T0,T1)+…

(12)

(13)

将方程(12)~(13)代入方程(10)，利用多尺度方法，可以得到

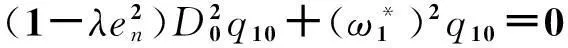
(14)

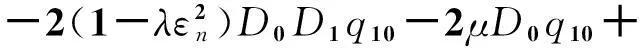
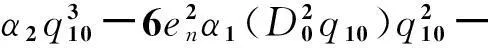
2gf1q10(T0-τ)

(15)

方程(14)的一阶近似解为

(16)

将方程(16)的解代入方程(15)，消除久期项，响应的幅值a和相位γ取决于如下控制方程的极坐标形式：

D1a=-μea+Qsinγ

(17)

aD1γ=σea+vea3+Qcosγ

(18)

γ=σT0-β.

显然，通过增加时滞与反馈控制参数两类控制因子，反馈增益和时滞调整了平均方程的参数. 非局部效应参数对阻尼系数和调谐系数有明显的影响. 因此，通过选择最佳反馈控制增益和时滞，可以达到所期望的控制效果.

令D1a=D1γ=0，得到

-μea+Qsinγ=0

(19)

σea+vea3+Qcosγ=0

(20)

根据方程(19)和(20)，频率响应方程表示成

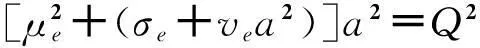
(21)

响应的幅值是调谐参数、时滞、反馈控制增益以及激励幅值的函数.

从方程(21)中得到的主共振响应的峰值振幅可以写成

(22)

作为比较，无控制的非线性主共振的峰值振幅为

(23)

在减小振动控制器的非线性振动特性时，由于非线性系统很难找到解析解，所以不能按照线性系统讨论响应幅值比的简单方法研究非线性系统. 因此，在有控制和无控制的非线性动力学系统中，利用衰减率即主共振峰值的比值来评价振动控制的效果.衰减率可以表示为

(24)

2 碳纳米管梁主共振振动控制器的设计

方程(23)和(24)相应的雅可比矩阵的特征值决定了解的稳定性.相应的特征值是下列方程的根

(25)

方程(25)的两个特征值和为-2μe.若μe>0，两个特征值的和始终是负的，两个特征值中至少有一个特征值始终有负实部.根据上述分析，保证系统稳定的充分条件是

μe>0

(26)

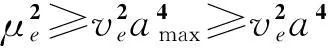
(27)

可得到稳定振动控制磁场的范围，即

μ]}1/2

(28)

若方程f(σe)=0有两个解，即

(29)

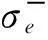
(30)

(31)

考虑σe的表达式和(30)式，得到稳定振动控制磁场的范围为

μe>0

(32)

考虑式(31)，有

μe>0

(33)

3　 碳纳米管梁控制器参数优化设计分析

通过非线性振动系统的稳定条件分析可以得出反馈控制参数的范围，但是无法获得系统最优的反馈控制参数. 以衰减率作为目标函数，利用最优化方法得到最优的反馈控制参数.

3.1特征方程无解时参数的优化设计

(34)

3.2 特征方程有两个解时参数的优化设计

(35)

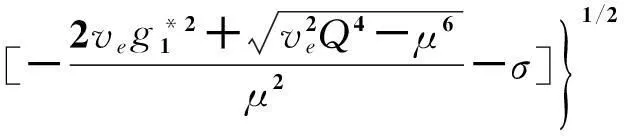
或者

μe>0

4　仿真分析

将碳纳米管视为Euler-Bernoulli梁模型，对纵向磁场作用下单壁碳纳米管的非线性振动进行研究和讨论，设计算例.单壁碳纳米管的直径d=7nm，壁厚h=0.68nm，长度L=140nm，质量密度ρ=2 300kg·m-3，阻尼系数η=1×10-6Nsm-1.

图1为主共振峰值amax在不同控制磁场Hx作用下与时滞和反馈控制增益的变化关系曲线.e0取值为3nm.由图1可知，amax随着时滞的变化而变化.对于固定的反馈控制增益，通过选择一个最佳时滞，可以得到最小的振动幅值.当时滞为一个固定值时，增加反馈控制增益可以降低峰值振幅.

图1　主共振峰值amax在不同控制磁场Hx作用下与时滞和反馈控制增益的变化关系曲线

图2表示衰减率R在不同非局部效应参数下与时滞和反馈控制增益的变化关系曲线.由图2可见，当非局部效应参数数值变大时，衰减率数值减小，因而，考虑非局部效应是必要的. 较大的反馈控制增益可以得到较小的衰减率R，表明增大反馈控制增益的数值可以取得较好的减振控制效果. 通过选择适当的时滞和反馈控制增益可以得到较小的衰减率R.当反馈控制增益是一个固定值时，最小衰减率R可以通过选择一个最佳时滞得到.

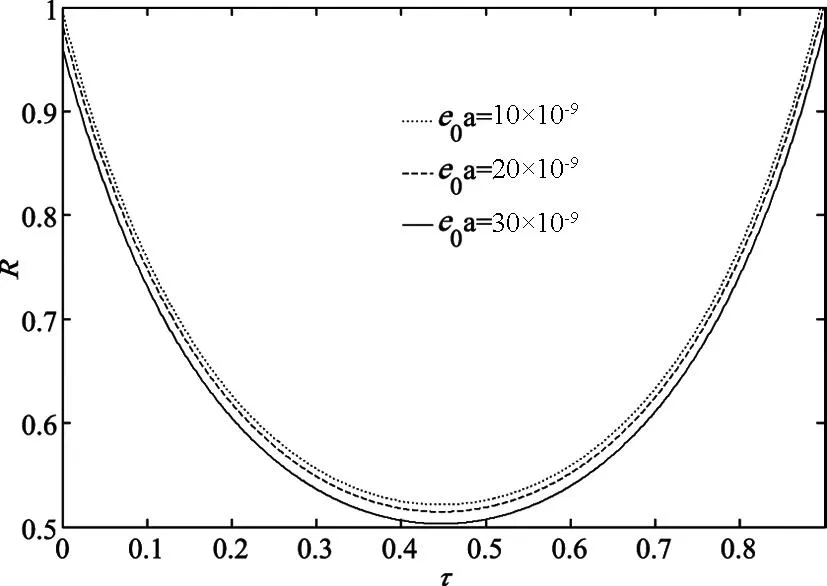
图2　 衰减率R在不同非局部参数下与时滞 和反馈控制增益的变化关系曲线

图3显示了调谐阻尼μe在不同控制磁场Hx作用下与时滞和反馈控制增益的变化关系曲线. e0取值为3nm. 由图可见，μe随着时滞的变化而变化.对于固定的反馈控制增益，通过选择一个最佳时滞可以得到最大的阻尼值.当时滞为一个固定值时，增加反馈控制增益可以降低峰值振幅.选择适当的时滞和反馈控制增益Hx可以得到较小的峰值振幅amax.

图3　调谐阻尼μe在不同控制磁场Hx作用下与　　时滞和反馈控制增益的变化关系曲线

图4给出了三组不同非局部效应参数的稳定控制磁场与时滞的变化关系曲线.曲线上方区域为稳定控制磁场区域，曲线下方区域为非稳定控制磁场区域. 非局部效应参数对控制磁场的取值有一定影响，非局部效应参数越大，控制磁场的取值越小.

图4　三组不同非局部效应参数的稳定控制磁场与时滞的变化关系曲线

5 结束语

利用磁场反馈时滞控制器对单壁碳纳米管系统主共振进行减振控制.基于梁的弯曲理论，建立考虑非局部效应的褶皱变形碳纳米管动力学微分方程.由本征值方程的稳定条件得到具有稳定解的控制磁场取值范围. 以碳纳米管非线性振动的衰减率为目标函数，以稳定区域的反馈增益为约束条件，利用最优化方法计算得到最优化反馈控制增益，得到最优的控制磁场强度等.研究了非局部效应参数对控制系统参数影响. 设计最优化控制器对碳纳米管系统的非线性振动进行减振控制.

参考文献:

[1]Iijima S. Helical microtubules of graphitic carbon[J]. Nature, 1991, 354:56-58.

[2] Gibson R F, Ayorinde E O， Wen Y F. Vibrations of carbon nanotubes and their composites: a review[J]. Composites Science and Technology, 2007, 67:1-28.

[3] Ramezani A, Alasty A， Akbari J. Closed-form solutions of the pull-in instability in nano-cantilevers under electrostatic and intermolecular surface forces[J]. International Journal of Solids and Structures, 2007, 44(14/15): 4 925-4 941.

[4] Ramezani A, Alasty A， Akbari J. Analytical investigation and numerical verification of Casimir effect on electrostatic nano-cantilevers[J]. Microsystem Technologies, 2008, 14:145-157.

[5] Zhang W, Baskaran R，Turner K L. Effect of cubic nonlinearity on auto-parametrically amplified resonant MEMS mass sensor[J]. Sensors and Actuators A: Physical,2002,102(1-2):139-150.

[6] 杨晓东, 林志华. 利用多尺度方法分析基于非局部效应纳米梁的非线性振动[J]. 中国科学(技术科学), 2010, 40(2):152-156.

[7] Wang C M, Kitipornchai S， Lim C W. Beam bending solutions based on nonlocal Timoshenko beam theory[J]. Journal of Engineering Mechanics, 2008, 134(6):475-481.

[8] Ke L L,Xiang Y. Yang J. Nonlinear free vibration of embedded double-walled carbon nanotubes based on nonlocal Timoshenko beam theory[J]. Computational Materials Science,2009, 47(2):409-417.

[9] Yang J, Ke L L， Kitipornchai S. Nonlinear free vibration of single-walled carbon nanotubes using nonlocal Timoshenko beam theory[J]. Physica E. 2010, 42(5):1 727-1 735.

[10] Mehdipour I, Soltani P Ganji D D. Nonlinear vibration and bending instability of a single-walled carbon nanotube using nonlocal elastic beam theory[J]. International Journal of Nanoscience, 2011, 10(3):447-453.

[11] Wang H, Dong K, Men F,etal. Influences of longitudinal magnetic field on wave propagation in carbon nanotubes embedded in elastic matrix[J]. Applied Mathematical Modelling, 2010, 34(4):878-889.

[12] Narendar S,Gupta S S， Gopalakrishnan S. Wave propagation in single-walled carbon nanotube under longitudinal magnetic field using nonlocal Euler Bernoulli beam theory[J]. Applied Mathematical Modelling, 2012, 36(9):4 529-4 538.

[13] Murmu T, McCarthy M A， Adhikari S. Vibration response of double-walled carbon nanotubes subjected to an externally applied longitudinal magnetic field: A nonlocal elasticity approach[J]. Journal of Sound and Vibration, 2012, 331(23):5 069-5 086.

[14] Wang X, Wang X Y，Xiao J. A non-linear analysis of the bending modulus of carbon nanotubes with rippling deformations[J]. Composite Structures,2005, 69(3):315-321.

(编辑：刘宝江)

Magnetic delayedoptimal control of carbon nanotube

considering nonlocal effect

XU Ying-zi, YUE Shu-chang, LIU Can-chang, LIU Lu, JING Dong

( School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255049, China)

Abstract:An optimal control method is presented for the magnetic delayed control of the nonlinear vibration of beams considering nonlocal elastic effect. Taking the attenuation ratio as the objective functions and the regions of feedback parameters as constraint conditions, considering the influence of nonlocal elastic parameters, the optimal feedback control parameters can be calculated by using optimal method. The control performance of control system is improved by selecting the optimal time delay. The influence of the nonlocal elastic parameters on the control parameters and time delay is studied. The simulation is designed to analyze the vibration control.

Key words:nonlinear vibration;control; optimal method;response;time delay

中图分类号：O332； O328 文献标志码：A

文章编号：1672-6197(2015)04-0006-05

作者简介：许英姿，女， xuyz@sdut.edu.cn1

基金项目：国家自然科学基金资助项目(51275280)

收稿日期：2014-09-20