——纪念广义相对论诞生100周年

蔡志东1 ,葛宇宏2

(1.镇江高等专科学校 丹阳师范学院，江苏 丹阳 212300；

2.南京科技职业学院 基础教学部，江苏 南京 210048)



度规张量的几何意义和物理意义

——纪念广义相对论诞生100周年

蔡志东1,葛宇宏2

(1.镇江高等专科学校 丹阳师范学院，江苏 丹阳 212300；

2.南京科技职业学院 基础教学部，江苏 南京 210048)

摘要：度规张量是广义相对论的核心,要想真正理解广义相对论,必须首先理解度规张量.系统论述了度规张量的几何意义和物理意义以及它的一些重要特性, 利用度规张量的意义和等效原理可以快速确定史瓦西度规.

关键词：度规张量；基矢；张量势；赝引力势

度规张量究竟表示什么？为什么它能随意升降张量的指标？迄今为止，尚未见到有人对此作出系统的论述，本文将用通俗易懂的语言系统回答这些问题.

1　张量的三种定义

首先介绍一下张量的一般定义：若有一个物理量,有a个上标λ1,λ2…λa,b个下标σ1,σ2…σb,每个指标均可以从1取到n,如果每一个上指标(逆变指标)均按照逆变矢量的变换规律而变,每一个下指标(协变指标)均按照协变矢量的变换规律而变,则该物理量就称之为a阶逆变,b阶协变,总阶数为(a+b)阶的混合张量,其变换规律为

(1)

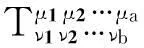
(2)

2　度规张量的定义及其对称性

黎曼认为,在n维空间中,无限靠近的两点之间的距离平方可以表示为：ds2=gμ νdxμdxν,它不随坐标系的变换而变,是一个坐标变换的不变量或标量(这样的空间称之为黎曼空间),其中的gμ ν定义为黎曼空间的(协变)度规张量,简称为协变度规.事实上,因dxμ,dxν均为逆变矢量,所以根据张量的外积定义(张量可以看成矢量的外积)可知,dxμdxν=dxνdxμ为二阶逆变对称张量.由张量的内秉定义可得：gμ ν为二阶协变张量.容易证明：对称张量和反对称张量的内积必为零.所以度规张量gμ ν和对称张量dxμdxν的内积只有其对称部分有贡献,因此，我们一般认为度规张量gμ ν为对称张量(事实上,这一性质可直接由它的意义得到).

3　度规张量具有升降指标的作用

AμAμ=λμ νAμAν=R=g0k1k2ds2=

g0k1k2gμ νdxμdxν=g0gμ ν(k1dxμ)(k2dxν)

(3)

4　度规张量的几何意义

4.1混合度规张量的特性及n维空间中距离微元平方ds2的最一般表示

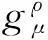
根据上面所述,度规具有升降指标的作用,由此我们可以写出n维空间中,无限靠近的两点之间的距离微元平方ds2的最一般表达式

ds2=gμ νdxμdxν=dxνdxν=dxμdxμ=

gμ νdxμdxν=dxνdxν=dxμdxμ=

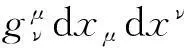
(4)

4.2度规张量的几何意义

4.2.1协变度规的几何意义

迄今为止,很少见到有人能对度规张量的几何意义和物理意义作出系统的解释,这对初学者而言,是一个极大的障碍,是跨入广义相对论大门的最大绊脚石.

众所周知,选择不同的坐标系实际上就是选择不同的基矢，在球坐标系中(r,θ,φ),设3个正交方向的单位矢量分别为：er,eθ,eφ,则空间任意两个无限邻近的点之间的矢量为ds=drer+rdθeθ+rsinθdφeφ=(er)dr+(reθ)dθ+(rsinθeφ)dφ=αrdr+αθdθ+αφdφ,其中αr=er,αθ=reθ,αφ=rsinθeφ为3个方向的基矢,由此得ds2=ds·ds=(αr·αr)dr2+(αθ·αθ)dθ2+(αφ·αφ)dφ2=dr2+r2dθ2+r2sin2θdφ2.根据度规的定义可知,g11=grr=α1·α1=αr·αr=1,g22=gθθ=α2·α2=αθ·αθ=r2,g33=gφφ=α3·α3=αφ·αφ=r2sin2θ,其他交叉项gij=αi·αj=0(i≠j).

不失一般性,在任意n维非正交曲线坐标系中,无限靠近的两点之间的空间矢量可以表示为ds=αμdxμ=ανdxν,因此,ds2=ds·ds=(αμdxμ)·(ανdxν)=(αμ·αν)dxμdxν,与黎曼的定义式：ds2=gμ νdxμdxν相比较,立即可得

(5)

特别声明,上式中相同指标不表示求和(广义相对论中,只有上下指标相同才表示求和),θμ ν为xμ,xν两个曲线坐标轴相交于某点的两个切向基矢之间的夹角.此公式极其重要,它表明,度规张量的几何意义是：非正交曲线坐标系中,任意两个坐标轴上的“切向基矢的点积”构成的张量, 每个分量的大小由相邻两个轴之间的夹角以及相邻两个轴上的基矢的长度确定.因此,度规张量能够准确反映曲线坐标系对平直坐标系的偏离情况.对四维时空而言,度规张量能够准确反映时空的弯曲情况.

4.2.2逆变度规和混合度规的几何意义

弯曲空间在无限小范围内可以近似看作平直空间,正如曲线坐标系在无限小范围内可以近似看作平直坐标系一样.在这样一个近似的线性空间中,任意一个微元矢量ds可以有无数种表示方法.选择不同的基矢就有不同的坐标.现在我们选择一组基矢(协变基矢)(αμ)=(α1,α2…,αn),在这一组协变基矢下,微元矢量ds在每个坐标轴上的坐标分别为(dxμ)=(dx1,dx2…,dxn),它构成n维空间的逆变矢量.即：ds=αμdxμ,ds2=(αμ·αν)dxμdxν=gμ νdxμdxν.现在我们另取一组基矢(逆变基矢)：(βν)=(β1,β2…,βn),在这一组逆变基矢下,微元矢量ds在每个坐标轴上的坐标分别为(dxv)=(dx1,dx2…,dxn)，它构成n维空间的协变矢量,此时有：ds=βνdxν=βμdxμ,ds2=ds·ds=(βμdxμ)·(βνdxν)=(βμ·βν)dxμdxν=gμ νdxμdxν,由此得

(6)

式(6)中的θμ ν为坐标xμ,xv在某点切向基矢之间的夹角(注意因为都是上标,所以相同指标不表示求和).式(6)表明：逆变度规张量可以看成两个“逆变基矢的点积”构成.

下面我们讨论混合度规张量,这是真正的关键所在.根据上面的讨论,显而易见有

(7)

式(7)是一个极其重要的关系式,它表明：逆变基矢βμ和协变基矢αν之间满足克罗内克关系,因此,我们可以从一组基矢导出另外一组基矢,或者说从一个坐标架构导出另一个坐标架构.再次强调一下：协变基矢对应逆变坐标微元矢量,逆变基矢对应协变坐标微元矢量,协变度规由两个协变基矢点积而成,逆变度规由两个逆变基矢点积而成.

两组基矢之间的关系可以用一个简单的图表示,图1以三维非正交曲线坐标为例,表示了两组基矢之间的关系.其中的(α1,α2,α3)为非正交的3个协变基矢(虚线表示),而(β1,β2,β3)为3个逆变基矢(实线表示).

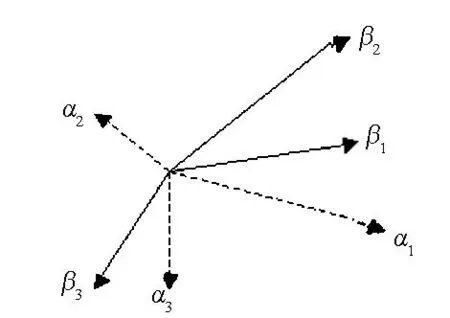
图1　协变基矢和逆变基矢关系图

根据图1,我们可以非常清楚地知道：“为什么度规张量能够随意地升降张量的指标？”,原因在于,张量可以看成矢量的外积,而矢量可以有两种表示方法,在协变基矢下为逆变矢量,在逆变基矢下为协变矢量.所谓“升降指标”实际上就是同一个东西(矢量或张量)用不同的方法表示而已.

4.2.3度规张量的基本性质

根据上面的讨论,特别是根据图1,立即可得度规张量的两个重要性质：

(1)它是对称张量(因αμ·αν=αν·αμ,βμ·βν=βν·βμ,所以gμ ν=gν μ,gμ ν=gν μ)

(2)在任意正交曲线坐标系中,只有非交叉项不为零,交叉项gμ ν=0(μ≠ν).正因为如此,所以在直角坐标系、球坐标系和柱坐标系中,均只有非交叉项如g11,g22,g33等.

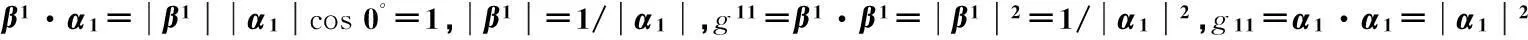
4.2.4狭义相对论中不分逆变和协变的原因

5　度规张量的物理意义

通过和电磁场的比较,可以清楚地知道度规张量的物理意义.众所周知,电磁场可以用电场强度E和磁感应强度B来描述,也可以用四维势Aμ=(A1,A2,A3,iφ/c)描述.当用场强E、B描述时,电磁场方程就是麦克斯韦方程组(两对四个),分别为

(8-1)

(8-2)

当我们用四维势Aμ描述时,实际上这两对方程可以合并为两组关于Aμ的二阶偏微分方程.令电磁场张量为：Fμ ν=∂Aν/∂xμ-∂Aμ/∂xν则式(8)中的两对方程可分别写为[5]：

(9-1)

或

(9-2)

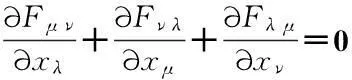
(10-1)

或

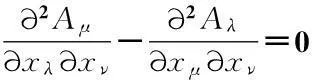
(10-2)

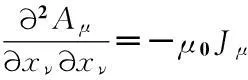
(11)

式(11)中的□=∂2/∂xν∂xν为洛伦兹标量算符,说明真正有用的方程是式(11),确定了Aμ,场强E和B均可以确定.由此可知,电磁场方程无非就是关于Aμ的4个二阶偏微分方程而已.

类似地,引力场可以用场强g描述,也可以用“引力场的势”描述.在爱因斯坦引力场方程Rμ ν-gμ νR/2=κTμ ν中,左边的里奇张量Rμ ν和曲率标量R均是由黎曼曲率张量通过缩并而得,所以它们都包含了度规对时空坐标的二阶和一阶偏导数,所以场方程是关于gμ ν或gμ ν的二阶非线性偏微分方程组.和电磁场比较,我们可以知道,度规相当于引力场的势.

但是,“引力势”既非电势那样的标量势,也非磁势那样的三维矢量势,而是具有16个分量的张量势(只有10个独立).它比用场强g描述引力场要好千万倍,能够真正全面地反映引力场的分布和它对时空的影响.知道了度规张量,也就知道了引力势的时空结构,引力场的一切性质以及它对时空的影响就能了如指掌.度规之所以具有“势“的特点,还因为势具有一定的不确定性(势能或势是相对的),而度规也是这样.把度规的各个分量都扩大或缩小若干倍,不影响引力场的性质.度规分量之间的内在联系是绝对的,但是数值是相对的.

在正交曲线坐标系中,引力场的“张量势”只有4个分量.一般情况下,由于时空互相影响,必须用16个分量的“张量势”才能准确描述引力场的特性.

6　利用度规张量的意义和等效原理快速确定史瓦西度规

迄今为止，所有的相对论专著在求解“静态球对称的真空引力场方程的解”——即所谓的Schwarzschild(史瓦西)外解时，都是采用直接求解爱因斯坦引力场方程，从而获得史瓦西度规的.这种方法繁琐复杂，笔者利用度规张量的意义和等效原理，能够快速确定史瓦西度规.下面详述其过程.

第一步，根据度规的几何意义，它表示曲线坐标轴上的切向基矢之点积.由于静态球对称引力场不随时间而变，因此，这意味着时间坐标轴和三维空间坐标轴是正交的(因为时间变化时，空间分量可以不变，所以时间轴和空间轴必然互相垂直).另一方面，由于引力场仅沿着径向分布，不影响角向，因此，空间部分可采用球坐标(r,θ,φ)来描述.这样，4个坐标轴都是互相正交的.根据度规的几何意义，立即可得：史瓦西度规只有4个分量不为零即：g11,g22,g33,g44(取x4=ict)或g00,g11,g22,g33(取x0=ct)，其余所有交叉项gμ ν=0(μ≠ν).

第二步，根据引力场具有球对称性和上面的讨论，可以大致确定史瓦西度规的形式为：ds2=g11dr2+g22dθ2+g33dφ2+g44d(ict)2，由于引力场不影响角向的度规或引力势，因此中心对称的引力场的度规分量g22,g33与无引力时的真空度规完全一致，即有g22=r2，g33=r2sin2θ.于是，我们只需要确定度规分量g11,g44即可.

第三步(最关键的一步)，利用等效原理，无限小范围内，引力场等效于一个加速参照系(它会产生惯性力场).设想一个电梯从无穷远处开始在球对称引力场中向着球心自由下落，则在电梯内，一切物体都将处于完全失重状态.因此，这样的一个变加速系可以完全等效引力场，即引力场对时空的一切影响和一个“由无穷多个瞬时惯性系构成的变加速参照系”完全一致(这些瞬时惯性系均沿着径向向球心运动).于是广义相对论中的引力问题就转化为了(无限小时空范围内的)狭义相对论问题.众所周知，狭义相对论中有

ds2=dr2/(1-v2/c2)+r2dθ2+r2sin2θdφ2+

(1-v2/c2)(icdt)2

(12)

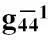
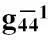
很多人会提出疑问，认为这个是在弱场低速下导出的，未必适合强场高速.下面，笔者将对此作出解释.当电梯从无穷远处向引力中心(球心)下落时，电梯的速度越来越大，同时引力场也越来越强.在最一般的情况下，可以假定物体的动能和速度之间呈一种复杂的函数关系：T=T(v2)(写成这种形式是考虑到动能和速度的方向无关，±v对应的动能相同，所以没有写成T=T(v)).根据级数理论，无论多么复杂的函数，只要令自变量小于1，总可以把它展开成无穷级数：即T=T0+T1(v2)+[T2(v4)+T3(v6)+…Tn(v2n)+…]，其中的T0为速度v=0时的动能(零点动能，一般认为是零)，T1(v2)为速度较小(高次项可以忽略)时的经典动能T1(v2)=m0v2/2.其他高次项(方括号中的项)为速度较高时相对论性修正项.根据狭义相对论，满足洛伦兹变换的动能为

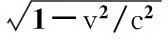
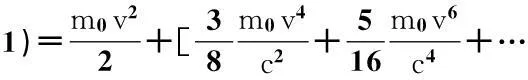
与此相似，满足洛伦兹变换的引力势能无论它和半径r的关系多么复杂，总可以写成U=U+U1(1/r)+[U2(1/r2)+U3(1/r3)+…Un(1/rn)+…]，其中的U为无穷远处的势能(通常假定它为零).U1(1/r)为离开引力中心较远距离处的经典势能(高次项可以忽略)，即牛顿引力势能：U1(1/r)=-Gm0M/r，当离开中心较近时，引力势能将不再符合牛顿公式，需要加上一个额外的相对论性修正项，即U表达式中的方括号项.如果我们假定在无穷远处电梯的动能为零，引力势能也为零，则在此后下落的任意一时刻，由于能量守恒，其总能量仍然为零，即

E=T+U=[T0+U]+[T1(v2)+U1(1/r)]+

(13)

式(13)中右边的第1个方括号为零，第2个方括号在较远距离处为零，因而第3个方括号在较远距离处也为零.理所当然地，在较近距离处，第3个括号也为零，因此在较近距离处，第2个方括号仍然为零.即强场高速下，仍然有v2=2GM/r. 因而我们得出的史瓦西度规具有普遍的意义.

总而言之，了解度规张量的几何意义和物理意义不仅对理解广义相对论非常重要，而且在实际的应用中也有用处.

参考文献:

[1]须重明 吴雪君.广义相对论与现代宇宙学[M].南京：南京师范大学出版社,1999.

[2]赵峥 刘文彪.广义相对论基础[M].北京：清华大学出版社,2010.

[3]赵峥.广义相对论入门讲座连载④—度规张量[J].大学物理,2011,30(10)：60-61.

[4]梁灿彬 周彬.微分几何入门与广义相对论:上册[M].北京：科学出版社,2006.

[5]郭硕鸿.电动力学[M].北京：高等教育出版社,1997.

[6]冯麟保 刘雪成 刘明成.广义相对论[M].长春：吉林科学技术出版社,1995.

(编辑：郝秀清)

Geometricandphysicalmeaningofthemetrictensor

——Tocommemoratethe100anniversaryofthebirthofgeneralrelativity

CAIZhi-dong1,GEYu-hong2

(1.DanyangNormalCollege，ZhenjiangCollege,Danyang212300,China;

2.DepartmentofBasicScience,NanjingPolytechnicInstitute,Nanjing210048,China)

Abstract:Metric tensor is the core of the general theory of relativity.To truly understand the general theory of relativity,we must understand the meaning of metric tensor.The system discussed the geometric and physical meaning and some of its important characteristics of the metric tensor. Using the significance of metric tensor and principle of equivalent，we can quickly determines the Schwarzschild’s metric tensor.

Key words:metric tensor; the basic vector; tensor potential; counterfeit gravitational potential

中图分类号：O412.1

文献标志码：A

文章编号：1672-6197(2015)04-0025-06

作者简介：蔡志东,男,czd196261@sina.com

基金项目：江苏省教育科学“十二五”规划2013年度重点课题(B-b/2013/03/071)；镇江高等专科学校科研团队资助项目(ZJCKYTD 20 )

收稿日期：2014-09-30