沈炳良， 刘 玲

(1.上海财经大学浙江学院 公共基础教育部,浙江 金华 321013;2.浙江师范大学 数理与信息工程学院,浙江 金华 321004)

1001-5051(2012)04-0368-07

群交叉积构造的一类新的Hopf群余代数

沈炳良1， 刘 玲2

(1.上海财经大学浙江学院 公共基础教育部,浙江 金华 321013;2.浙江师范大学 数理与信息工程学院,浙江 金华 321004)

探讨了群交叉积C#πσH和群Smash余积C×πH构成半Hopf群余代数乃至Hopf群余代数的条件,这是著名的Radford双积在Hopf群余代数系统中的实现.

(半)Hopf群余代数;群交叉积;群Smash余积;Radford双积

0 引 言

1985年,Radford[1]证明了Smash积A#H和Smash余积A×H(其中A为一个左H-模代数,且为左H-余模余代数)构成Hopf代数的充要条件是:A为范畴HHYD中的一个Hopf代数.此定理被称为Radford双积定理.2010年,Andruskiewitsch等[2]通过此 Hopf代数对有点Hopf代数进行了分类.由此可见Radford双积定理的重要性.对于Radford双积已经有诸多形式的推广,如拟Hopf代数的Radford双积[3]、弱Hopf代数的Radford双积[4]、乘子Hopf代数的Radford双积[5]等等.

Hopf群余代数是由Turaev[6]引进的对Hopf代数的一种重要推广,它是Turaev在进行拓扑量子场论的研究工作时发现的一种代数结构.Caenepeel等[7]给出了Hopf群余代数的另一种解释,即它是某种特殊的对称张量范畴(称之为Turaev 范畴)上的Hopf代数.值得注意的是,由于Hopf群余代数的不对称性必然会打破Hopf代数的自对偶性,因此,推广时需要一定的处理技巧与复杂的计算,这也激发了人们对Hopf群余代数中的一些课题比较感兴趣.关于Hopf群余代数的知识,可参考文献[8-13]等.

本文主要讨论Ranford双积在Hopf群余代数中的情形,并由此构造出一类新的Hopf群余代数.

1 基本定义

本文中,k表示一个固定的域,所有的工作将在k上展开.总是假定π是一个有单位元1的抽象群,⊗和Hom分别表示为⊗k和Homk.如果U和V是2个k-向量空间,那么TU,V:U⊗V→V⊗U表示一个扭曲映射,定义为TU,V(u⊗v)=v⊗u,∀u∈U,v∈V.对代数A和余代数C,有卷积代数Conv(C,A),定义在向量空间Hom(C,A)上,其乘法为

(f*g)(c)=mA(f⊗g)ΔC(c)=f(c1)g(c2).

其中:∀f,g∈Hom(C,A);∀c∈C.

定义1[6,8]π-余代数(群余代数)是一簇k-向量空间C={Cα}α∈π,同时带有一簇k-线性映射Δ={Δα,β:Cαβ→Cα⊗Cβ}α,β∈π(称为余乘)和k-线性映射ε:C1→k(称为余单位),使得Δ在下列意义下是余结合的:

(Δα,β⊗idCγ)Δαβ,γ=(idCα⊗Δβ,γ)Δα,βγ,对任意α,β,γ∈π;

(idCα⊗ε)Δα,1=idCα=(ε⊗idCα)Δ1,α,对任意α∈π.

对余乘使用Sweedler记法[14],即Δα,β(c)=c(1,α)⊗c(2,β),∀α,β∈π,c∈Cαβ.

定义2[6,8]Hopfπ-余代数(Hopf 群余代数)是一个带有一簇k-线性映射S={Sα:Hα→Hα-1}α∈π(称为反对极)的π-余代数H=({Hα},Δ,ε),使得:

1)每个Hα是带有乘法mα和单位元1α∈Hα的代数;

2)ε:H1→k和Δα,β:Hαβ→Hα⊗Hβ都是代数同态,∀α,β∈π;

3)对每个α∈π,mα(Sα-1⊗idHα)Δα-1,α=ε1α=mα(idHα⊗Sα-1)Δα,α-1.

若π-余代数H只满足1)和2),则称其为半Hopfπ-余代数(半Hopf群余代数).

注意(H1,m1,11,Δ1, 1,ε,S1)是一个Hopf代数.上述定义中的一套公理不是自对偶的.Hopf群余代数H的反对极S={Sα}α∈π被称为是双射,如果每一个Sα都是双射.Hopfπ-余代数H的反对极S既是代数反同态,又是余代数反同态,即对任意α,β∈π,a,b∈Hα,

Sα(ab)=Sα(b)Sα(a),Sα(1α)=1α-1;

Δβ-1,α-1Sαβ=THα-1,Hβ-1(Sα⊗Sβ)Δα,β,εS1=ε.

定义3设H是(半)Hopfπ-余代数,A为k上的代数.称H弱作用在A上,如果存在一簇线性映射5:Hα⊗A→A,h⊗a|→h5a,∀α∈π,h∈Hα, 使得

1)1α5a=a,∀a∈A,α∈π;

2)h5(ab)=(h(1, α)5a)(h(2,β)5b),∀h∈Hαβ,a,b∈A;

3)h51A=ε(h)1A,∀h∈H1.

进一步,如果对每个α∈π,A是Hα-模,且满足条件2)和3),那么称A为左π-H-模代数.

定义4设H是(半)Hopfπ-余代数,A为k上的代数,且H弱作用在A上,设σ:H1⊗H1→A为一k-线性映射,定义A⊗H={A⊗Hα}α∈π.对每个A⊗Hα,定义其乘法如下:

(a⊗h)(b⊗g)=a(h(1,1)5b)σ(h(2,1),g(1,1))⊗h(3,α)g(2,α).

如果每个A⊗Hα是带有单位元1A⊗1α的结合代数,那么称A⊗H为π-交叉积,记为A#πσH.

由文献[15]得到A#πσH成为π-交叉积的一些充分必要条件.

命题1A#πσH是π-交叉积当且仅当

σ(11,h)=ε(h)1A=σ(h,11),∀h∈H1,其中11是H1的单位;

(h(1,1)5(g(1,1)5a))σ(h(2,1),g(2,1))=σ(h(1,1),g(1,1))(h(2,1)g(2,1)5a);

σ(h(1,1),g(1,1))σ(h(2,1)g(2,1),k)=(h(1,1)5σ(g(1,1),k(1,1)))σ(h(2,1),g(2,1)k(2,1)).

2 Radford双积H

本节将探讨π-交叉积C#πσH和π-Smash余积C×πH构成半Hopfπ-余代数乃至Hopfπ-余代数的条件.

定义5[11,13]设C={Cα}α∈π是π-余代数,V是k-向量空间.左π-C-余模似对象是一个二元组V=(V,ρV={ρVα}),其中,对任意α∈π,ρVα:V→Cα⊗V是k-线性映射(余模似结构),记为ρVα(v)=v(-1,α)⊗v(0,0),使得以下条件满足:

1)V是余可换的,即对任意α1,α2∈π,有

(idCα1⊗ρVα2)ρVα1=(Δα1,α2⊗idV)ρVα1α2,

也就是,v(-1,α1)⊗v(0,0)(-1,α2)⊗v(0,0)(0,0)=v(-1,α1α2)(1,α1)⊗v(-1,α1α2)(2,α2)⊗v(0,0)v(-2,α1)⊗v(-1,α2)⊗v(0,0),∀v∈V,α1,α2∈π.

2)V是余单位的,即(ε⊗idV)ρV1=idV.

下面给出左群余模余代数的定义.

定义6设H是Hopfπ-余代数,且C为k上的余代数.称C为左π-H-余模余代数,若以下条件成立:

1)C为左π-H-余模似对象;

2)c(-1,α)⊗c(0,0)1⊗c(0,0)2=c1(-1,α)c2(-1,α)⊗c1(0,0)⊗c2(0,0),∀α∈π,c∈C;

3)c(-1,α)ε(c(0, 0))=ε(c)1α,∀α∈π,c∈C.

设C是带有余模似结构映射ρ={ρα:C→Hα⊗C}α∈π的左π-H-余模余代数.π-Smash余积C×πH={C×Hα}α∈π定义在一簇k-向量空间{C⊗Hα}α∈π上,其余乘由以下公式给出:

Δα,β(c×h)=c1×c2(-1,α)h(1,α)⊗c2(0, 0)×h(2,β),∀c∈C,h∈Hαβ.

不难证明C×πH是π-余代数,其余单位是εC⊗εH1.

设H是半Hopfπ-余代数,(C,ΔC,εC)为左π-H-余模余代数,且(C,mC,μC)是代数,H弱作用在C上,σ:H1⊗H1→C是线性映射并且卷积可逆.设ρ={ρα:C→Hα⊗C}α∈π和5α:Hα⊗C→C分别为余模似和弱作用结构映射.定义C⊗H={C⊗Hα}α∈π作为向量空间.本节将着重给出使C⊗H成为半Hopfπ-余代数的充分必要条件.其中C⊗H的代数和π-余代数结构分别由π-交叉积C#πσH和π-Smash余积C×πH给出.如果(C⊗H,μC#πσH,mC#πσH,εC×πH,ΔC×πH)是半Hopfπ-余代数,那么称三元组(H,C,σ)是相容的,并记为C×π#πσH.

定义7设C#πσH是π-交叉积.称σ为扭曲余模余循环的,如果

c1⊗c2(0, 0)⊗c2(-1,α)h=c1σ(c2(-1,α)(1,1),h(1,1))⊗c2(0,0)⊗c2(-1,α)(2,α)h(1)

对所有c∈C,h∈Hα和α∈π成立.

本文总假设σ是扭曲余模余循环的.

引理1设C#πσH是带有σ扭曲余模余循环的π-交叉积,且C×πH是π-Smash余积,则有

(c1⊗c2)ε(h)=c1σ(c2(-1,1),h)⊗c(2)

对所有c∈C,h∈H1成立.

现在给出使C⊗H成为半Hopfπ-余代数的充要条件,其结构已在上文给出.

定理1设H是半Hopfπ-余代数,C既是左π-H-余模余代数又是代数,且H弱作用在C上.设C#πσH是带有扭曲余模余循环σ的π-交叉积,且C×πH为上文所定义的π-Smash余积,则以下结论是等价的:

1)C×π#πσH是半Hopfπ-余代数.

2)下列条件成立:

①σ(h,l)1⊗σ(h,l)2=σ(h(1,1),l(1,1))⊗σ(h(2,1),l(2,1)),ε(σ(h,g))=ε(h)ε(g);

②εC(h5c)=εC(c)εH1(h);

③εC是代数同态;

④Δ(ac)=a1(a2(-1,1)(1,1)5c1)σ(a2(-1,1)(2,1),c2(-1,1))⊗a2(0,0)c2(0,0);

⑤(h(1,1)5b)(-1,α)h(2,α)⊗(h(1,1)5b)(0,0)=h(1,α)b(-1,α)⊗h(2,1)5b(0,0);

⑥(h5a)1⊗(h5a)2=(h(1,1)5a1)σ(h(2,1),a2(-1,1))⊗h(3,1)5a2(0,0);

⑦h(1,α)l(1,α)⊗σ(h(2,1),l(2,1))=σ(h(1,1),l(1,1))(-1,α)h(2,α)l(2,α)⊗σ(h(1,1),l(1,1))(0,0);

⑧ΔC(1C)=1C⊗1C;

⑨ρα(ac)=ρα(a)ρα(c)且ρα(1C)=1α⊗1C.

证明 先证1)⟹2).假设C×π#πσH是半Hopfπ-余代数,那么余单位是代数同态,于是

ε((a⊗h)(b⊗g))=ε(a(h(1,1)5b)σ(h(2,1),g(1,1))⊗h(3,1)g(2,1))=

εC(a(h(1,1)5b)σ(h(2,1),g(1,1)))εH(h(3,1)g(2,1))=

ε(a⊗h)ε(b⊗g)=ε(a)ε(b)ε(h)ε(g),

∀h,g∈H1.令h=g=11,得εC(ab)=εC(a)εC(b),即③成立.

取a=1C,g=11,可得ε(h5b)=ε(h)ε(b),即②成立.

另取a=b=1C,立得ε(σ(h,g))=ε(h)ε(g),得①后半部分成立.

其次,因为Δα,β也是代数同态,所以对任意a,b∈C和h,g∈Hαβ,有

Δα,β((a×h)(b×g))=

Δα,β(a(h(1,1)5b)σ(h(2,1),g(1,1))⊗h(3,αβ)g(2,αβ))=

[(a(h(1,1)5b)σ(h(2,1),g(1,1)))1×(a(h(1,1)5b)σ(h(2,1),g(1,1)))2(-1,α)h(3,α)g(2,α)]⊗

[(a(h(1,1)5b)σ(h(2,1),g(1,1)))2(0,0)×h(4,β)g(3,β)],

且

Δα,β(a×h)Δα,β(b×g)=

[(a1×a2(-1,α)h(1,α))⊗(a2(0, 0)×h(2,β))]⊗[(b1×b2(-1,α)g(1,α))⊗(b2(0,0)×g(2,β))]=

[a1(a2(-1,α)(1,1)h(1,1)5b1)σ(a2(-1,α)(2,1)h(2,1),b2(-1,α)(1,1)g(1,1))×

a2(-1,α)(3,α)h(3,α)b2(-1,α)(2,α)g(2,α)]⊗[a2(0,0)(h(4,1)5b2(0,0))σ(h(5,1),g(3,1))×h(6,β)g(4,β)].

如果令a=b=1C和h=g=1α,那么有ΔC(1C)=1C⊗1C和ρα(1C)=1α⊗1C.即⑧和⑨的后半部分成立.

若取a=b=1C和h,g∈Hα,则

σ(h(1,1),g(1,1))1⊗σ(h(1,1),g(1,1))2(-1,α)h(2,α)g(2,α)⊗σ(h(1,1),g(1,1))2(0,0)⊗h(3,1)g(3,1)=

σ(h(1,1),g(1,1))⊗h(2,α)g(2,α)⊗σ(h(3,1),g(3,1))⊗h(4,1)g(4,1).

(3)

式(3)两边同时作用ε⊗id⊗id⊗ε,可得

h(1,α)g(1,α)⊗σ(h(2,1),g(2,1))=σ(h(1,1),g(1,1))(-1,α)h(2,α)g(2,α)⊗σ(h(1,1),g(1,1))(0,0),

即⑦成立.

若取h,g∈H1,且式(3)两边同时作用id⊗ε⊗id⊗ε,则

σ(h,g)1⊗σ(h,g)2=σ(h(1,1),g(1,1))⊗σ(h(2,1),g(2,1)),

即①的前半部分成立.

因为Δα,β(a×h)Δα,β(b×g)=Δα,β((a×h)(b×g)),令a=1C,g=1α且h∈Hα,所以

(h(1,1)5b)1⊗(h(1,1)5b)2(-1,α)h(2,α)⊗(h(1,1)5b)2(0,0)⊗h(3,1)=

(h(1,1)5b1)σ(h(2,1),b2(-1,α)(1,1))⊗h(3,α)b2(-1,α)(2,α)⊗h(4,1)5b2(0,0)⊗h(5,1).

(4)

式(4)两边同时作用εC⊗id⊗id⊗ε,可得

(h(1,1)5b)(-1,α)h(2,α)⊗(h(1,1)5b)(0,0)=h(1,α)b(-1,α)⊗h(2,1)5b(0,0),

即⑤成立.

若取h∈H1,且在式(4)两边同时作用id⊗ε⊗id⊗ε,即得⑥成立.

若令h=g=1α,又因为Δα,β是代数映射,于是

(ab)1⊗(ab)2(-1,α)⊗(ab)2(0,0)=

a1(a2(-1,α)(1,1)5b1)σ(a2(-1,α)(2,1),b2(-1,α)(1,1))⊗a2(-1,α)(3,α)b2(-1,α)(2,α)⊗a2(0,0)b2(0,0).

(5)

式(5)两边同时作用εC⊗id⊗id,得(ab)(-1,α)⊗(ab)(0,0)=a(-1,α)b(-1,α)⊗a(0,0)b(0,0).也就是ρα(ab)=ρα(a)ρα(b),从而⑨的前半部分也成立.

取g=h=11,并在式(5)两边同时作用id⊗ε⊗id,可以证明④成立.

再证 2)⟹1).假设2)成立,那么由2)中的①,②和③有

ε((a⊗h)(b⊗g))=ε(a⊗h)ε(b⊗g),∀h,g∈H1,a,b∈C.

由⑧和⑨得,Δα,β(1C⊗1αβ)=1C⊗1α⊗1C⊗1β.

为了证明Δα,β((a⊗h)(b⊗g))=Δα,β(a⊗h)Δα,β(b⊗g),只需证明对每个a,b∈C和h,g∈Hαβ,有

事实上,

Δα,β((a⊗1)(b⊗g))=Δα,β(ab⊗g)=

Δα,β((ab⊗1)(1⊗g))=Δα,β(ab⊗1)Δα,β(1⊗g)=

Δα,β(a⊗1)Δα,β(b⊗1)Δα,β(1⊗g)=Δα,β(a⊗1)Δα,β(b⊗g);

Δα,β((a⊗h)(1⊗g))=Δα,β((a⊗1)(1⊗h)(1⊗g))=

Δα,β(a⊗1)Δα,β((1⊗h)(1⊗g))=

Δα,β(a⊗1)Δα,β(1⊗h)Δα,β(1⊗g)=

Δα,β((a⊗1)(1⊗h))Δα,β(1⊗g)=

Δα,β(a⊗h)Δα,β(1⊗g);

Δα,β((a⊗h)(b⊗g))=Δα,β((a⊗1)(1⊗h)(b⊗1)(1⊗g))=

Δα,β(a⊗1)Δα,β((1⊗h)(b⊗1)(1⊗g))=

Δα,β(a⊗1)Δα,β((1⊗h)(b⊗1))Δα,β(1⊗g)=

Δα,β(a⊗1)Δα,β(1⊗h)Δα,β(b⊗1)Δα,β(1⊗g)=

Δα,β(a⊗h)Δα,β(b⊗g).

接下来将证明式(6)～式(9)成立.

Δα,β(a⊗1)Δα,β(b⊗1)=

[(a1×a2(-1,α))⊗(a2(0,0)×1β)][(b1×b2(-1,α))⊗(b2(0,0)×1β)]=

[a1(a2(-1,α)(1,1)5b1)σ(a2(-1,α)(2,1),b2(-1,α)(1,1))×a2(-1,α)(3,α)b2(-1,α)(2,α)]⊗

[a2(0,0)b2(0,0)×1β]=

[a1(a2(-1,1)(1,1)5b1)σ(a2(-1,1)(2,1),b2(-1,1))×a2(0,0)(-1,α)b2(0,0)(-1,α)]⊗

[a2(0,0)(0,0)b2(0,0)(0,0)×1β]=

(ab)1×(ab)2(-1,α)⊗(ab)2(0,0)×1β=Δα,β((a⊗1)(b⊗1));

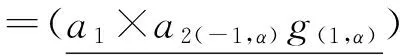
Δα,β(a⊗1)Δα,β(1⊗g);

Δα,β((1⊗h)(b⊗1))=Δα,β(h(1,1)5b⊗h(2,αβ))=

[(h(1,1)5b)1×(h(1, 1)5b)2(-1,α)h(2,α)]⊗[(h(1,1)5b)2(0,0)×h(3,β)]=

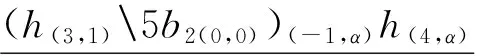
(h(1,1)5b1)σ(h(2,1),b2(-1,1))⊗h(3,α)b2(0,0)(-1,α)⊗h(4,1)5b2(0,0)(0,0)⊗h(5,β)=

(h(1,1)5b1)σ(h(2,1),b2(-1,α)(1,1))⊗h(3,α)b2(-1,α)(2,α)⊗h(4,1)5b2(0,0)⊗h(5,β)=

Δα,β(1⊗h)Δα,β(b⊗1);

Δα,β(1⊗h)Δα,β(1⊗g)=

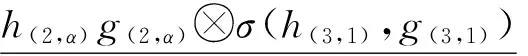
σ(h(1,1),g(1,1))⊗σ(h(2,1),g(2,1))(-1,α)h(3,α)g(3,α)⊗σ(h(2,1),g(2,1))(0,0)⊗h(4,β)g(4,β)=

σ(h(1,1),g(1,1))1⊗σ(h(1,1),g(1,1))2(-1,α)h(2,α)g(2,α)⊗σ(h(2,1),g(2,1))2(0,0)⊗h(3,β)g(3,β)=

Δα,β((1⊗h)(1⊗g)).

即式(6)～式(9)成立.定理1证毕.

注11)如果定理1中的σ是平凡的,那么就得到使π-Smash积和π-Smash余积成为半Hopfπ-余代数的充要条件.

2)如果C为平凡的左π-H-余模余代数,即ρα(c)=1α⊗c,那么π-Smash余积的余乘就退化为一般的张量积的余乘,即Δα,β(a×h)=(a1×h(1, α))⊗(a2×h(2,β)).由定理1,可以得到文献[15]中的命题2.4.

3)如果令π={1},那么定理1就是文献[16]中的定理 2.5.

接着将研究上文中的半Hopfπ-余代数C×π#πσH形成Hopfπ-余代数的条件.

定义8设H是半Hopfπ-余代数,C为余代数,σ:H1⊗H1→C是一线性映射,且S={Sα:Hα→Hα-1}是一簇线性映射并满足Δβ-1,α-1Sαβ=THα-1,Hβ-1(Sα⊗Sβ)Δα,β.称S为H的σ-反对极,若对每个h∈H1,有

在此情况下,称H为σ-Hopfπ-余代数.

使用Sweedler记法,式(10)意味着

σ(h(1,1),S(h(4,1)))⊗h(2,α)Sα-1(h(3,α-1))=ε(h)(1C⊗1α).

例1设H是带有反对极S={Sα}α∈π的Hopfπ-余代数,假设σ:H1⊗H1→k是平凡的线性映射,那么可以将S看作H的σ-反对极.

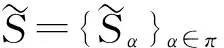
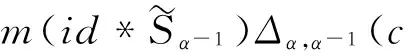
ε(h)(c1⊗1α)(SC(c2)⊗1α)=ε(h)εC(c)(1C⊗1α).

[1]Radford D E.The structure of Hopf algebras with a projection[J].J Algebra,1985,92(2):322-347.

[2]Andruskiewitsch N,Schneider H J.On the classification of finite-dimensional pointed Hopf algebras[J].Ann Math,2010,171(2):375-417.

[3]Bulacu D,Nauwelaerts E.Radford′s biproduct for quasi-Hopf algebras and bosonization[J].J Pure and Applied Algebra,2002,174(1):1-42.

[5]Delvaux L.Multiplier Hopf algebras in categories and the Biproduct construction[J].Algebra Represent Theory,2007,10(6):533-554.

[6]Turaev V G.Homotopy field theory in dimension 3 and crossed group-categories[EB/OL].(2000-05-31)[2011-09-15].http://arXiv:math/0005291v1.

[7]Caenepeel S,de Lombaerde M.A categorical approach to Turaev′s Hopf group-coalgebras[J].Comm Algebra,2006,34(7):2631-2657.

[8]Virelizier A.Hopf group-coalgebras[J].J Pure and Applied Algebra,2002,171(1):75-122.

[9]Virelizier A.Graded quantum groups and quasitriangular Hopf group-coalgebras[J].Comm Algebra,2005,33(9):3029-3050.

[10]Wang Shuanhong.Group entwining structures and group coalgebra Galois extensions[J].Comm Algebra,2004,32(9):3417-3436.

[11]Wang Shuanhong.Group twisted smash products and Doi-Hopf modules forT-coalgebras[J].Comm Algebra,2004,32(9):3437-3458.

[12]Zunino M.Double construction for crossed Hopf coalgebra[J].J Algebra,2004,278(1):43-75.

[13]Zunino M.Yetter-Drinfeld modules for crossed structures[J].J Pure and Applied Algebra,2004,193(1/2/3):313-343.

[14]Sweedler M.Hopf algebras[M].New York:Benjamin,1969.

[15]Shen Bingliang,Wang Shuanhong.On group crossed products[J].Int Electron J Algebra,2008(4):177-188.

[16]Wang Shuanhong,Jiao Zhengming,Zhao Wenzheng.Hopf algebra structures on croseed products[J].Comm Algebra,1998,26(4):1293-1303.

OnconstructingnewHopfgroupcoalgebrasbygroupcrossedproducts

SHEN Bingliang1, LIU Ling2

(1.DepartmentofBasicEducation,ShanghaiUniversityofFinanceEconomicsZhejiangCollege,JinhuaZhejiang321013,China; 2.CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

The group crossed productC#πσHand the group Smash coproductC×πHform a semi-Hopf group coalgebra and even a Hopf group coalgebra was discussed. It was famous Radford biproduct construction in the setting of Hopf group coalgebras.

(Semi)-Hopf group coalgebra; group crossed product; group Smash coproduct; Radford biproduct

2012-03-17

浙江省教育厅科研项目(Y201121955)

沈炳良(1981-),男,浙江德清人,讲师,博士后.研究方向:Hopf代数;代数表示论.

O153.3

A

(责任编辑 陶立方)