王宗尧，姜红燕，朱红波

（淮阴工学院数理学院，江苏 淮安223003）

1 矩估计法的基本思想及理论依据

矩估计法是最古老的求估计的方法之一，它是由英国统计学家K.Pearson 在1900年提出的.其基本思想是用样本矩及其函数估计相应的总体矩及其函数，理论依据是辛钦大数定律.

定理1［1］（辛钦大数定律）设随机变量X1，X2，…，Xn，…相互独立，服从同一分布，且具有数学期望E（Xi）=μ（i=1，2…），则对于任意正数ε，有:

辛钦大数定律告诉我们，样本1 阶原点矩依概率收敛于总体1 阶原点矩.

定理2［2］设随机变量X1，X2，…，Xn，…相互独立，服从同一分布，且具有数学期望E（）=μk（k=1，2，…），则对于任意正数ε，有:

由定理2 可知，样本k 阶原点矩依概率收敛于总体k 阶原点矩.这样，样本k 阶原点矩是总体k 阶原点矩的相合估计.根据依概率收敛的序列的性质，可以得到，其中g为连续函数，.因此样本k 阶原点矩的函数也是总体k 阶原点矩的函数的相合估计，故矩估计一般都具有相合性.所以矩估计法在统计学中具有广泛的应用.

2 矩估计的方法及计算步骤

用样本k 阶原点矩作为总体k 阶原点矩的估计量，建立含有待估参数的方程并解出待估参数.一般分布中有几个未知参数，就求到几阶矩.例如:

例1 设总体X 的数学期望μ和方差σ2都存在，试求μ，σ2的矩估计量.

解 设X1，X2，…，Xn为总体X 的样本，由题设:

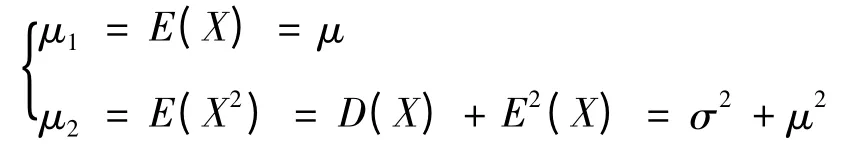
解得μ=μ1，σ2=μ2－.用A1，A2分别替换式中的μ1，μ2，即求得μ，σ2的矩估计量:

3 矩估计法的优点及不足

矩估计法的优点非常明显，简单易行，众人都能接受，使用场合甚广，且在总体分布未知时也可使用，如上述例1.一般来讲，若总体中的未知参数有k 个，则要求总体的前k 阶矩存在.当然，矩估计法的不足也有很多，本文在文献［3］的基础上，进行更加具体深入的讨论如下.

1）矩估计有时会得到不合理的解

例2［4］设总体X 服从区间［0，θ］上的均匀分布，其中θ ＞0 是未知参数，求θ 的矩估计量.

解 设X1，X2，…，Xn为总体X 的样本，由题设:

若抽取了一个容量为3 的样本，观测值分别为1，2，9.代入到后可得=8，，即总体X 服从区间［0，8］上的均匀分布.这样，样本值都应在区间［0，8］中，它们取值的上界不应超过8.但注意到样本观测值中的9 已落在［0，8］外，这显然是不合理的.这道题里，未知参数出现在总体所有可能取值的边界上，即未知参数界定了总体取值的范围.这一类问题称之为门槛参数问题.对于这类问题，一般来说用矩估计法求出的参数估计量往往不太合理.用极大似然估计法可以有效解决此类问题.

2）矩估计量不惟一

例3 设总体X 服从指数分布，密度函数为f（x）=λe－λx（x ＞0），求λ 的矩估计量.

解 设X1，X2，…，Xn为总体X 的样本，由题设:

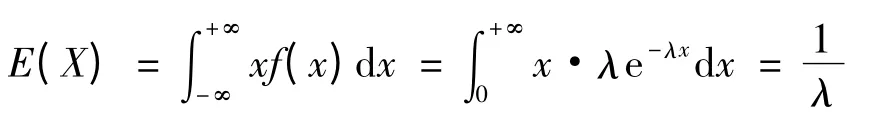
当矩估计不惟一时，涉及到的矩的阶数应尽可能小，从而对总体的要求也尽可能少.常用的矩估计一般只涉及一、二阶矩.当然，有时总体的一阶矩虽然存在，但是不含有待估参数，这时就要计算总体的二阶矩了（见例题4）.

解 设X1，X2，…，Xn为总体X 的样本，由题设:

不含待估参数θ，为此，又有:

3）矩估计法不一定可行

矩估计法在使用时要求总体的k 阶矩存在（这里k 小于等于待估参数的个数）.然而有些分布的总体矩并不存在，这样矩估计法就失效了.例如柯西分布的概率密度为，总体的各阶矩皆不存在，因此不能用矩估计法来估计参数θ.事实上，柯西分布概率密度更一般的形式为:

柯西分布以数学期望和方差均不存在而著名.

4 有关矩估计法的两点说明

1）如前所述，矩估计法的基本思想是用样本矩及其函数估计相应的总体矩及其函数，这里的矩是原点矩.然而由于总体的k 阶中心矩

总可以展开成总体的不超过阶的原点矩的函数，而样本的k 阶中心矩

可展成样本不超过k 阶原点矩的同样函数，因此可以用样本的k 阶中心矩作为总体k 阶中心矩的估计量.例如前面的例1，要估计总体的方差σ2，也即总体的二阶中心矩，就可以用样本二阶中心距来估计σ2，即:

这个结果和前面是一样的.因此矩估计法的基本思想可以重新阐述成“用样本k 阶原点矩（或中心矩）及其函数估计相应的总体k 阶原点矩（或中心矩）及其函数”.上述例3 中，由于总体二阶中心矩，故可以用样本二阶中心距来替换D（X），从而得到λ 的又一个矩估计.

2）当矩估计不惟一时，就必须对这些估计的好坏给出评价标准.有一个基本标准是所有的估计都应该满足的，它是衡量一个估计是否可行的必要条件，这就是矩估计的相合性.前面已经提到，矩估计一般都具有相合性.在这个基础上，评价一个点估计的好坏使用的度量指标总是点估计值与参数真值θ 的距离的函数，由此可以得到均方误差MSE（）=E（－θ）2的概念.自然，我们希望估计的均方误差越小越好.然而，可以证明:使均方误差一致达到最小的最优估计是不存在的.所以，通常是先对估计提出一些合理性要求，然后在满足这种合理性要求的估计类中寻找好的估计.无偏性便是一种最常用的合理性要求［5］.如果是θ 的无偏估计，则MSE（）=D（），此时用均方误差评价点估计与用方差是完全一样的，这也说明了用方差考察无偏估计有效性是合理的.当不是θ 的无偏估计时，就要看其均方误差.当然，在均方误差的含义下，有些有偏估计优于无偏估计［6］，这里不再赘述.

［1］郭跃华，朱月萍.概率论与数理统计［M］.北京:高等教育出版社，2011:132.

［2］范光，李广明.矩估计法的理论注释［J］.十堰职业技术学院学报，2012，25（1）:98－100.

［3］张永利.矩估计的基本原理及其解题方法［J］.巢湖学院学报，2005，7（3）:47－49.

［4］夏宁茂，秦衍，倪中新.新编概率论与数理统计［M］.上海:华东理工大学出版社，2006:179－181.

［5］茆诗松，王静龙，濮晓龙.高等数理统计［M］.北京:高等教育出版社，1998:87.

［6］茆诗松，程依明，濮晓龙.概率论与数理统计教程［M］.北京:高等教育出版社，2004:295.