李 莉

（南京财经大学应用数学学院，江苏 南京210046 ）

引言

在微分方程的研究中，格林（Green）函数起着非常重要的作用，它可以用来求解弦振动［1］等动力问题.但在不同的文献中，Green 函数的求法是不统一的.本文研究二阶常微分方程

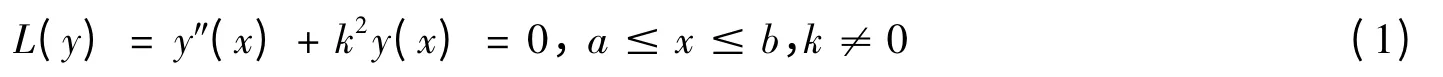
在多种边界条件［2］下的Green 函数.该方法可求出很多微分方程边值问题的Green 函数.

本文首先给出Green 函数的定义及其构造方法，其次是研究二阶常微分方程（1）在周期边界条件下的Green 函数，再次对相关的几种边界条件，直接给出所述问题的Green 函数，最后是算例.

1 Green 函数的定义［3］及其构造方法

给定二阶常微分方程（1）及边界条件:

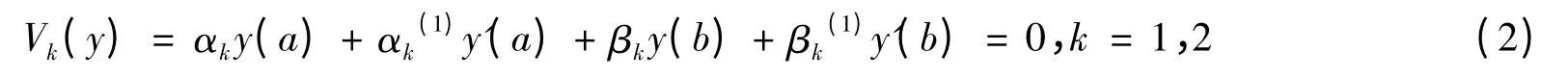
设y（a），y＇（a），y（b），y＇（b）的一次式V1，V2是线性独立的.

定义1 设ε为（a，b）中的任意点:a ＜ε ＜b ，具有以下4 个性质的函数G（x，ε），称为边值问题（1），（2）的Green 函数.

1）对每个固定的ε，G（x，ε）本身关于x 是连续的;

2）G（x，ε）关于x 的导数，以x = ε为第一类间断点，且跃度为－1，即

3）对于x ≠ε，函数G（x，ε）关于x 是二次可微的且满足常微分方程（1），即L［G］= 0;

4）对于x ≠ε，函数G（x，ε）关于x 满足边界条件（2），即Vk（G）= 0.

Green 函数的构造如下.

设y1（x），y2（x）是方程（1）的线性无关解.由性质3）知函数G（x，ε）在［a，ε）及（ε，b］上可由上述y1（x），y2（x）表出，即:

其中a1，a2，b1，b2是ε 的函数.

由性质1）知函数G（x，ε）在点x=ε 连续，故有［b1y1（ε）+b2y2（ε）］－［a1y1（ε）+a2y2（ε）］=0，又由性质2）有［b1y＇1（ε）+b2（ε）］－［a1（ε）+a2（ε）］=－1，设:

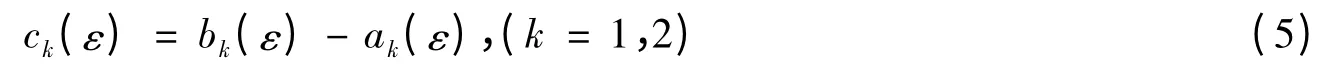
于是得到关于ck（ε）的线性方程组:

方程组（6）的系数行列式为Wronski 行列式W（y1（x），y2（x））在点x =ε 时的值，因为y1（x），y2（x）线性无关，所以W（y1（ε），y2（ε））≠0，故方程组（6）有唯一解ck（ε），（k=1，2）.

下求ak（ε），bk（ε）.将边界条件（2）中的Vk（y）写为:Vk（y）=Ak（y）+Bk（y），其中Ak（y）=αky（a）+αk（1）y＇（a ），Bk（y）=βky（b）+βk（1）y＇（b）.由式（4）得:

同理有Bk（G）=b1Bk（y1）+b2Bk（y2）.由性质4）可得Vk（G）=Ak（G）+Bk（G）=0.即:

又由式（5）知ak=bk－ck，则:

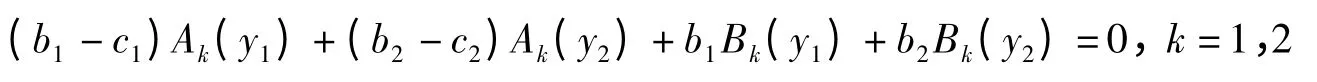
于是

方程组（7）为关于b1，b2的线性方程组，由V1，V2线性无关，知方程组的系数行列式:

因此，方程组（7）的解b1（ε），b2（ε）存在并且是惟一的.由ak=bk－ck（k=1，2）得知ak（ε）（k =1，2）也存在且惟一.将ak（ε），bk（ε）（k=1，2）代入式（4）就得到G（x，ε）.

上述过程证明了Green 函数的存在惟一性.于是有下面的引理1:

引理1 若边值问题（1），（2）只有零解y（x）≡0，则算子L 有且只有一个Green 函数.

2 周期边界条件下的Green 函数及其证明

首先设方程（1）具有周期边界条件:

我们有下列结论.

定理1 二阶边值问题（1），（8）的Green 函数为:

证明 我们已知方程（1）的基本解组为coskx，sinkx，则通解为y =Acoskx +Bsinkx，其中A，B为任意常数.由边界条件（8），可得A，B 满足下列等式:

从而可得A=B=0，故由引理1 知Green 函数存在且惟一.由基本解组（coskx，sinkx），可设Green 函数的形式如下:

其中a1，a2，b1，b2为ε 的待定函数.

设ck（ε）=bk（ε）－ak（ε），k=1，2.由方程组（6）可得关于ck（ε）的线性方程组:

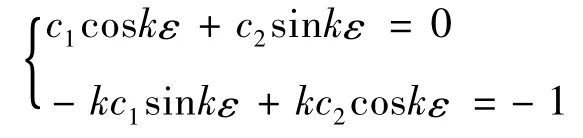
解得:

由性质4）知Green 函数应满足边界条件（2），则对问题（1），（8）应有G（a，ε）=G（b，ε），G＇（a，ε）=G＇（b，ε）.于是有:

由式（5），（12），（13）可得:

把所求系数ak，bk（k=1，2）代入式（10），（11），即得问题（1），（8）的Green 函数:

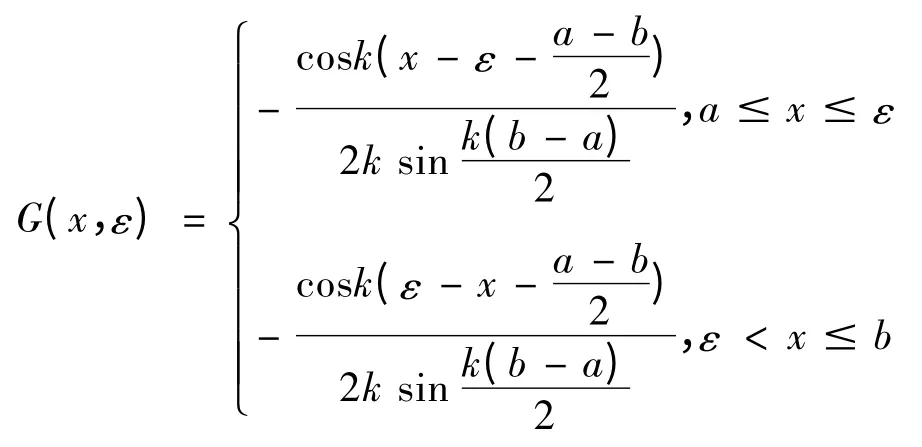
3 另外几种边界条件下的Green 函数

由于以下几种边界条件下的Green 函数的证明过程与周期边界条件下的Green 函数的证明类似，所以直接给出所述问题的Green 函数.

4 计算Green 函数的示例

在实际求Green 函数时，可直接套用公式，也可不直接用公式，而按照定理1 的证明过程也可以求出该类二阶常微分方程在不同边界条件下的Green 函数.

例1 求二阶常微分方程

在边界条件

下的Green 函数.

解 我们已知常微分方程（18）的通解为y（x）=Acosx+Bsinx，其中A，B为任意常数.

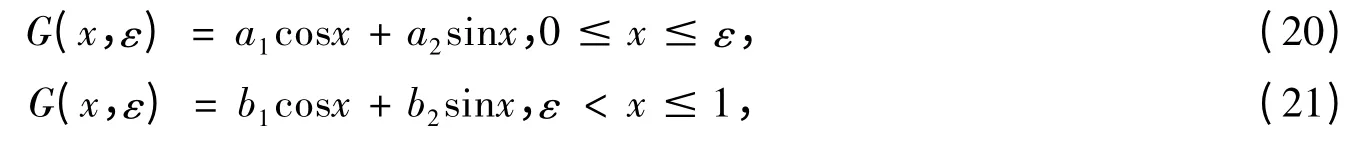
其中a1，a2，b1，b2为ε 的待定函数.

设ck=bk－ak，k=1，2.由方程组（6）可得关于ck（ε）的方程组，解之得:

因为Green 函数具有性质4），应满足边界条件（19），所以对问题（18），（19）成立:G（0，ε）=G（1，ε），G＇（0，ε）=G＇（1，ε），即:

由式（5），（22），（23）可得:

把所求得的系数代入式（20），（21），即得问题（18），（19）的Green 函数为:

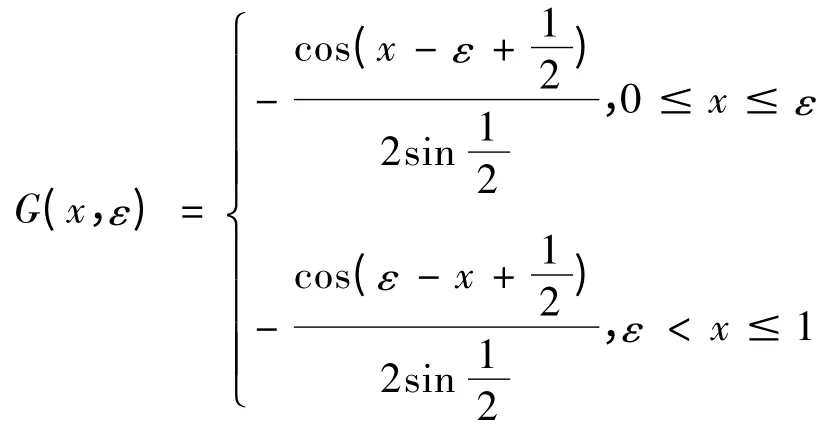
例2 求常微分方程（18）在边界条件y＇（0）=y（1）=0 下的Green 函数.

解 本题中k=1，a=0，b=1，利用公式（17）可得Green 函数为:

［1］韩茂安，周盛凡，邢业朋，等.常微分方程［M］.北京:高等教育出版社，2011:163－164.

［2］王高雄，周之铭，朱思铭，等.常微分方程［M］.第3 版.北京:高等教育出版社，2006:370－371.

［3］Pokornyi Y V，Borovskikh A V.the connection of the green’s function and the influence function for nonclassical problems［J］.2004，119（6）:739－768.