冯玉娴

《义务教育数学课程标准（2022 年版）》（以下简称“《课标》”）指出：初中阶段“图形与几何”领域的内容分为“图形的性质”“图形的变化”“图形与坐标”三个主题。初中生主要学习点、线、面、角、三角形、多边形和圆等几何图形，从演绎证明、运动变化、量化分析三个方面研究这些图形的基本性质和相互关系。“图形的性质”主要侧重学生对图形概念的理解，以及对基于概念的图形性质、关系、变化规律的理解，重点强调直观发现、整体联想、逻辑推理来研究图形；“图形的变化”强调从运动变化的观点来研究图形；“图形与坐标”强调数形结合，用代数方法研究几何图形[1]。因此，“图形的性质”是“图形与几何”领域的主干知识，是“图形的变化”“图形与坐标”的学习基础，是中考命题考查的核心内容。中考试题中通常是以单个图形或几个基本图形的组合图形为背景，考查图形的概念和性质的简单应用，注重基本图形的性质对图形中相关线段、角、局部等对象进行定性与定量的分析，以促进学生对图形的性质的全面理解和整体把握[2]。2023 年天津市中考落实《课标》的学业要求，既有传承又有创新。以下通过对试卷中第（17）题和第（21）题的详细剖析，阐述在图形中考查学生分析和解决问题的设计思路及分析方法。

一、试题评析

（一）关注图形，强化关联

（17）题：如图1，在边长为3的正方形ABCD的外侧，作等腰三角形ADE，且EA=ED=

（Ⅰ）△ADE的面积为__________；

（Ⅱ）若F是BE的中点，连接AF交CD于点G，则AG的长为__________.

1.考查意图解析

此题参考人教版数学教材八年级下册第十八章平行四边形复习题第1 题（3），将原题的等边三角形，变为腰与底边不相等的等腰三角形，将角的计算改为求线段长的问题，重点突出变中不变的规律，探寻图形中边、角两个重要组成要素之间的关系。考查正方形的性质、等腰三角形的性质、平行线分线段成比例的基本事实、全等三角形的判定和性质、勾股定理等数学知识，其中，灵活的运算能力是解决此题的重要因素。

本题涵盖正方形、等腰三角形、直角三角形、三角形的中位线、全等三角形等内容，关注学生在复杂图形中分解出基本图形的能力，是对学生的识图能力、推理能力的综合考查。强调了基本图形的基本性质、探究图形的基本要素之间的内在联系，这样有助于学生合理选择数学方法，养成良好的思维品质。抓住“关键要素”，探究相关联系是解决本题的重要思路。这样的设计，主要考查图形的主要要素之间的位置关系和数量关系，学生需要在新的图形情境中，借助几何直观分析问题。本题给学生预留很大的探索空间，学生在解决问题的过程中，可以体会多角度思考问题，发展推理能力。

2.解法分析

第（Ⅰ）问求△ADE的面积，需要求等腰△ADE底边的高EM，而EM在Rt△AME中，运用勾股定理得到EM=2。体现了等腰三角形中“见等腰作底边上的高”的通性通法。

第（Ⅱ）问求线段AG的长，首先考虑所求线段在什么图形中研究。按照“它是谁，在哪，与谁有关系”三个层次的思维方式思考，也就是说，所求的线段是哪个图形的组成要素，能在这个图形中求解吗？若图形的已知条件满足，可以直接求解；若已知条件不足，可以将缺少的要素转化至另一个可以求解的图形中。

【思路一：直击目标】

常见的分析方法是“执果索因”，即要求线段AG的长，发现图中AG在Rt△AGD中，AD的长是已知条件，因此转化为求GD的长的问题。

【方法1：借助轴对称构造全等三角形】

如图2，过点E作EM⊥AD，延长EM交AG于点N，由平行线分线段成比例的基本事实可知GD=2MN，转化为求MN的长。由F是BE中点，可以联想到△ABF≌△NEF，得到NE=AB=3，从而得出MN=1，进而计算出GD=2，由勾股定理得AG=。解决本题的关键是发现由正方形和等腰三角形组合而成的整体图形是轴对称图形，EM所在直线是对称轴，将第（Ⅰ）问和第（Ⅱ）问巧妙地建立联系，体现最优化最简洁的解题思路。

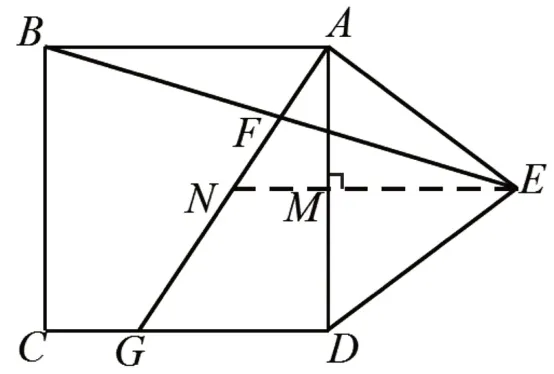
图2

【方法2：借助中点构造三角形的中位线】

如图3，由中点F，联想AF是哪个三角形的中位线。延长BA，使AH=BA=3，连接HE。将问题转化为关键点E与谁有关？分别延长HE和AE，与CD的延长线分别相交于点M、N。发现在Rt△ADN中，点E是斜边AN的中点，根据勾股定理得于是有△AEH≌△NEM，可知MN=3。由四边形AGMH是平行四边形可知GM=AH=3，从而计算出GD=2。回到基本图形Rt△AGD中，得这种方法看似烦琐，但是学生能从中点出发构造基本图形的思维方法是有意义的，凸显在复杂图形中识别基本图形的能力。

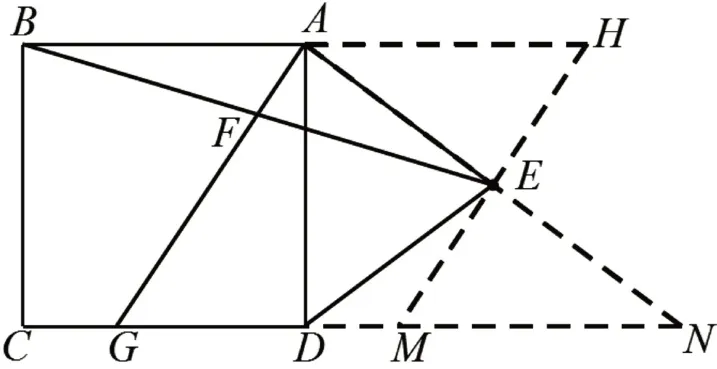
图3

【方法3：构造相似三角形】

如图4，由关键点E联想到构造相似三角形。延长CD、BE交于点H，点E作EM⊥CH，垂足为M。由BH。由AB∥GH得△ABF∽△GHF，有得GH=9。因为EM∥BC得△HEM∽△HBC，有得到MH=5，从而计算出GD=2，从而计算出有的学生对平行线分线段成比例的基本事实和相似三角形情有独钟，善于灵活运用到解题中，积累了丰富的数学活动经验，体现学生思维的广阔性。

图4

【教学建议】教学中，教师应引导学生发现图形的对称特点，帮助学生学会用整体的、联系的、发展的眼光看问题。运用第一种方法解决问题，凸显通性通法的重要性，这是中考考查的重点。学生只有积累了丰富的解题经验，才能在中考答题时游刃有余，避免将简单的问题复杂化。

【思路二：树木成林】

由树木见森林，由部分看整体是一种解题策略。AF是AG的一部分，可将求AG的长转化为求AF的长，或者转化为求AG的长。

【方法1：借助线段的倍分关系求解】

由于学生的思维存在差异，对于中点F所处的位置会产生不同的联想。如图2，发现AG=2AN，于是转化为求AN的长。在Rt△AMN中，由MN=1，AM=计算得，推出

【方法2：借助比例关系求解】

有的学生发现AG=AF+FG，重新构造新的直角三角形，分别求AF，FG的长。见到中点F，想到构造三角形的中位线是一种常见的思维方法。

如图5，过点作FM⊥BA，垂足为M。延长MF交CD于点N，过点作EH⊥BA，与BA的延长线交于点H。由根据勾股定理得。由AM∥GN得所以FG=3AF，进而AG=AF+FG=4AF=

图5

【教学建议】教学中，教师应善于拓宽学生的解题思路，引导学生从多角度思考问题，从整体问题的一部分切入，也是一种常见的思维方法。“借助线段倍分关系求解”与思路一“借助轴对称构造全等三角形”有异曲同工之处，区别在于放在不同的直角三角形求线段的长，体现直接求解和间接求解各自的优势，学生应该具备优化解题思路的能力。

【思路三：创设情境】

借助图形的特征，建立平面直角坐标系，将“图形的性质”转化为“图形与坐标”的问题，运用几何直观，从“形”和“数”两个方面进行思考，将求AG的长转化为求点A与点G之间的距离。

如图6，以C为原点，CD所在直线为x轴，CB所在直线为y轴。易得点，由于直线AF：y=kx+b过点A（3，3）、点，所以有

图6

这种解题思路对于初中生不常见，当学生发现图形形状的特殊性，且在平面直角坐标系中可以用坐标表示图形中点A、B、E的位置，学生能理解平面上的点与坐标之间的一一对应关系，才能想到用代数方法研究几何图形。在具体问题情境中，学生会从代数的角度分析和解决几何问题，体现数形结合思想，用坐标法分析和解决问题，是发展几何直观和创新意识的途径之一。

（二）多解归一，探寻本质

（21）在⊙O中，半径OC垂直于弦AB，垂足为D，∠AOC=60°，E为弦AB所对的优弧上一点.

（Ⅰ）如图7，求∠AOB和∠CEB的大小；

图7

（Ⅱ）如图8，CE与AB相交于点F，EF=EB，过点E作⊙O的切线，与CO的延长线相交于点G.若OA=3，求EG的长.

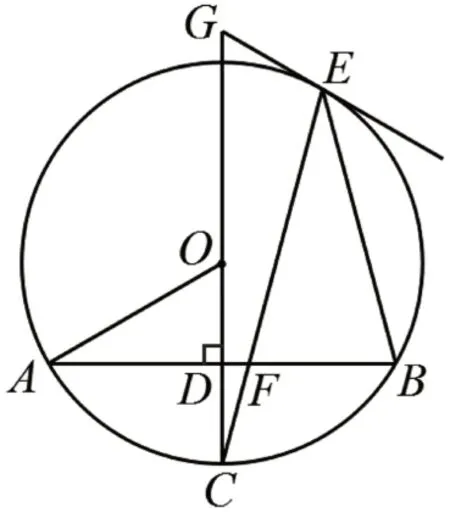
图8

1.考查意图解析

此题参考人教版数学教科书九年级上册习题24.1 第5 题，已知垂直于弦的半径，由圆心角的度数求出另一个圆心角∠AOB的度数和圆周角∠CEB的度数。题目中的点D是垂足，也是弦AB的中点，点E为弦AB所对的优弧上一点，将图7 和图8 有机融合，建立联系。又将问题拓展为直线与圆相切的位置关系，以切点为顶点构造等腰三角形BEF，从而求切线长GE。

本题将圆与等腰三角形、直角三角形有机结合，是一道以圆的有关知识为基础的几何图形计算题，考查学生的识图能力、几何直观、推理能力。本题结构鲜明，思路顺畅，重点考查圆周角定理、切线的性质、等腰三角形的性质、直角三角形的性质、三角形内角和定理、解直角三角形等知识。

2.解法分析

第（Ⅰ）问求角的度数，首先分析∠AOB是圆心角，是已知的圆心角∠AOC的2 倍，所求的圆周角∠CEB与圆心角∠BOC对着同一条弧，容易解决问题。

【思路一：“圆”来如此】

垂径定理是解决问题的关键，圆是一种曲线图形，它既是轴对称图形又是中心对称图形，因此借助圆的性质就能解决问题。由垂径定理得在同圆中，如果两条弧相等，那么它们所对的圆心角相等，所以得出∠AOC=∠BOC，进而得出∠AOB=2∠AOC=120°，根据圆周角定理有∠CEB=30°。

【思路二：对称之美】

由于等腰三角形是轴对称图形，探究得到等腰三角形的性质，它是解决本题的关键。由等腰三角形AOB的“三线合一”可知∠AOC=∠BOC，易得∠AOB=2∠AOC=120°，从而求出30°。

对比两种思路，图7 中两个基本图形垂径定理和等腰△AOB都能求∠AOB的度数，再运用圆周角定理求圆周角∠CEB的度数。第（Ⅰ）问重点考查基础知识和基本图形，学生可以从不同的角度思考，很容易求解。

第（Ⅱ）问求线段GE的长，GE在△GCE中无法求解，需要重新构造基本图形，将问题层层转化。GE是圆的切线，依据切线的性质，自然想到“见切线连半径”，连接OE有OE⊥GE。在Rt△OEG中，已知半径OE=3，斜边OG不可求，问题转化为求∠GOE或∠G的大小。问题逐步转化，由“要知”思考到“需知”，思路自然顺畅，合情合理[3]。

【思路一：自“圆”其说】

借助圆周角∠C求圆心角∠GOE的大小，这是圆中求圆心角的通性通法。

【方法1：运用等腰三角形的“等边对等角”求圆周角∠C】

如图9，等腰三角形的顶角和底角是重要要素，等腰三角形的两个底角相等，所以由顶角的度数知底角的度数，有∠EFB=75°，看到图中∠DFC和∠EFB是对顶角，问题转化为Rt△CDF中两个锐角互余，求得∠C=15°。由 圆 周 角 定 理 得∠GOE=2 ∠C=30°。∠GOE既是圆心角，又是直角三角形的一个锐角，架起两个图形之间的桥梁。在Rt△OEG中，tan∠GOE=

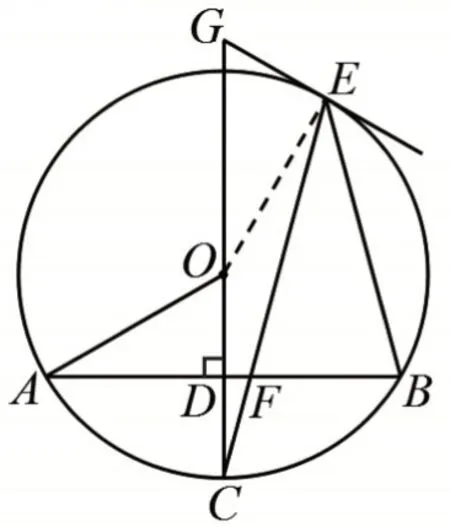
图9

【方法2：运用等腰三角形的“三线合一”求圆周角∠C】

如图10，连接OE，过点E作EM⊥FB，垂足为M。等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合，可知已知OC⊥AB，有OC∥EM，所以∠C=∠FEM=15°，进而∠GOE=2∠C=30°，所以

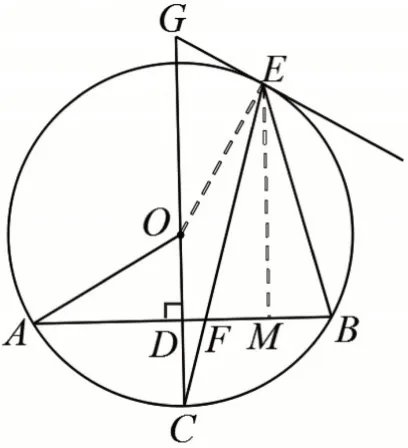
图10

【思路二：积沙成塔】

运用圆心角的和差关系求角，就是把相关的角逐一求出，最后运用这些角的位置关系和数量关系解决问题。

【方法1：圆周角是桥梁】

如图9，等腰三角形BEF的两个底角相等，求得∠EBF=∠EFB=75°。根据圆周角定理可知∠AOE=2∠EBF=150°，所以有∠GOE=∠AOE-∠AOG=30°，所以

【方法2：等腰直角三角形是桥梁】

如图11，连接OE、OB，易得∠OBE=∠EBF-∠OBF=45°，发现△BOE是等腰直角三角形，得∠BOE=90°，从而得到∠GOE=180°-∠BOE-∠COB=30°，所以EG=。辅助线OB将第（Ⅱ）问的图形转化为第（Ⅰ）问的图形，第（Ⅰ）问中的结论和解题方法是第（Ⅱ）问的基础和延续，让两个问题相辅相成、相得益彰。

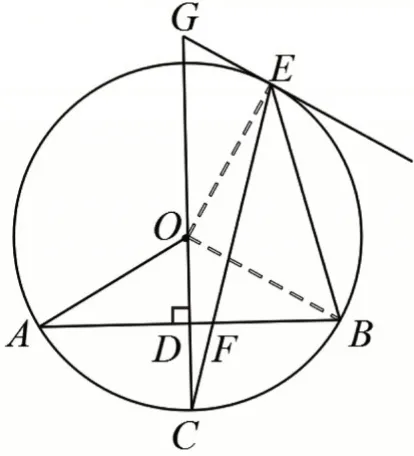
图11

【方法3：四边形是桥梁】

如图11，在四边形DBEG中，∠GDB=90°，∠DBE=75°，∠GEB=∠GEO+∠BEO=135°，可得∠G=60°，所以

【教学建议】基本图形在数学解题中有着举足轻重的作用，由于学生的知识储备、思考问题的方式不同，所以学生解决问题的策略和方向也就不同。从一题多解到多解归一，使解题经验升华到系统思维高度。教师要理解学生的所思所想，秉承“不同的人在数学上得到不同的发展”的数学课程基本理念，为不同学生的多样性发展提供空间[4]。这样的题目设计采用经典图形，注重学生对所学基础知识的理解，让学生体会数学知识之间的联系，发展几何直观和推理能力。

二、教学启示

（一）夯实基础，培养识图能力

掌握好基础知识、基本技能是从事高水平数学活动的保证，为学生形成高阶思维奠定坚实的基础。“图形的性质”强调通过实验探究、直观发现、推理论证来研究图形，学生应经历知识的发生、发展过程，明确“为什么学？”“是什么？”“有什么用？”“怎么用？”如，第（17）和（21）题中涉及的基础知识覆盖初中学段“几何与图形”领域的核心内容，涵盖三角形、四边形和圆等相关知识，学生应结合基本图形，从文字语言、符号语言和图形语言描述概念和性质。学生通过对第（17）和（21）题的图形结构进行再认识、新构思，才能形成解题策略。因此，教学中关注学生“怎样想到的”比“怎样解决的”更为重要。教师应帮助学生梳理知识结构，让知识之间建立联系，形成知识体系，加强核心知识的研究，理解并掌握通性通法。既要培养学生注重对基本图形的形的提炼、辨认、分离、联想和重构，也要注重培养学生对基本图形的探索、理解、诠释、感悟和内化，这样才能使学生的解题能力得到实质性的提升。

（二）积累经验，重视一般观念引领

章建跃博士说，数学教材的体系结构遵循“一定之规”，一般按“背景—定义—分类—性质—特例—联系”的逻辑展开。一般观念是指研究一个数学对象，首先要定义对象，再从定义出发研究性质。性质要研究的问题是对象的要素之间的关系、相关的重要元素之间的关系、对象之间的相互关系等。例如，等腰三角形是一种特殊的三角形，它除了具有一般三角形的所有性质外，还有许多特殊的性质，这些特殊的性质，都和它是轴对称图形有关，得出“等边对等角”“三线合一”等性质，并进一步讨论等腰三角形的判定方法以及等边三角形的性质与判定方法等内容。教学中，要重视对教学内容的整体分析，帮助学生建立能体现数学本质，整体把握学习“图形的性质”的主要脉络，突出“概念—性质—判定—联系—应用”的研究主线，让学生学会从特殊到一般，从一般到特殊，从具体到抽象的探究方法，在观察、实验、计算、操作、猜想、验证、推理中体会并运用数学思想与方法，积累数学的基本活动经验，逐步形成核心素养。

（三）全面联动，发展思维能力

思维是数学学习的核心，是发展能力的关键，是数学核心素养的重要体现，数学知识及其背后蕴含的数学思想方法，是提升和培养学生思维能力的重要载体。例如，第（21）题第（Ⅱ）问求线段的长，不同的学生对问题的思考角度不相同，因此解决问题的路径也就不相同。学生将问题转化为熟悉的基本图形，将未知转化为已知，将复杂的问题转化为简单的问题，充分体现转化是初中数学的核心思想。数学思想方法是对数学知识在更高层次上的抽象和概括，它具有总结性、实用性、规律性，也具备一定的基础性。数学思想的形成需要经历一个从模糊到清晰、从理解到应用的长期发展过程。学生只有经历了这样的过程，才能深刻体验、感悟、内化数学思想方法，从而真正地发展思维能力[4]。教学中，教师应精选、整合教材中相关内容，重视变式与创新，关注内容与能力共融的综合性问题，鼓励学生从多角度分析问题、解决问题，培养学生数学思维的灵活性、深刻性和广阔性，实现正向迁移，触类旁通，力求达到“做一题，会一类，通一片”的教学效果。通过一题多解、一题多变，不仅能够有效触发学生多角度、多方位地思考，更重要的是全面联动数学知识，促进数学知识体系的有效构建，提升关键能力，发展核心素养。

总之，在数学教学与评价中，教师应以《课标》为依据，在关注数学学习结果的同时，更要关注学生对思考问题、解决问题方法的提炼和归纳，让学生不仅“知其然”，还要“知其所以然”，达到“何由以知其所以然”。只有这样，学生无论遇到什么样的新问题和新题型，都能用数学的眼光、数学的思维、数学的语言从容应对，进一步发展推理能力和运算能力，增强应用意识和创新意识。