D 型Fock 空间与量子对称对
2023-08-21EHRIGMichael甘凯轩
EHRIG Michael,甘凯轩
(北京理工大学 数学与统计学院, 北京 102488)
本文研究的是LANINI 等[1]定义的组合Fock 空间在 so2N(C) 的情况.它与标量扩张下的 so2N(C)的有限维表示范畴的Grothendieck 群同构.本文将组合Fock 空间嵌入到由某些序列定义的空间中,这些序列来自经典的charge 0 Fock 空间.在这个空间上可以定义一个仿射量子对称对作用,仿射量子对称对的定义来自于KOLB[2].本文证明了这个作用与单位根处的量子群的邻接原理是相容的,并且用与研究A型Fock 空间上的量子对称对作用相似的方法描述了D 型Weyl 模的张量积分解.
1 预备知识
为了避免Dynkin 图太小的特殊情况,固定一个整数
1.1 李代数
令g=so2N(C) 是 C 上 的DN型 李 代 数.假 定N> 3,


根据文献[1]的1.1 节,D 型的组合Fock 空间F(DN)是一个 Q(v) 向量空间,它有一个基 λ|λ ∈X+.因为X+可以分解为X1,+∪X1/2,+,所以 F(DN)有分解
1.2 量子群
这一部分的定义来自于LUSZTIG[3].令
式中x,y为 Q(v)上不交换的变量,然后对1≤i,j≤N,令aij=(αj,αi)∈Z.
量子包络代数Uv(g) 是由 {Ei,Fi,|1 ≤i≤N}生成的 Q(v)上的结合代数,它的生成元满足如下生成关系(1≤i,j≤N):

用Uv(g) - mod 表示有限维1 型Uv(g)模的范畴,然后 用[Uv(g) -mod]表 示Uv(g)-mod 的Grothendieck 群,其上的标量从 Z 扩张到 Q(v).
与LUSZTIG[4]类似,用UA(g) 表示Uv(g)的A 形式,用Uq=UA(g)⊗AC 表示v特殊化为q∈C的情形.将Uq简单地称为一个单位根处的量子群.令Uq-mod 是有权空间分解的有限维Uq模的范畴,见TANISAKI[5]的第七章,用[Uq-mod]表示它的Grothendieck 群,其上的标量扩张到 Q(v).
根据TANISAKI[5]的第七章,对λ∈X+,定义UA(g)模DA(λ)是Uv(g) 的不可约最高权模Dv(λ)的A 形式.将v特殊化为q给出了Weyl模的定义:Dq(λ)=DA(λ)⊗AC.由ANDERSEN 等[6]的命题1.22,这三个模有相同的特征标,即
下面是张量积分解的重要结果.
命题1设λ,µ∈X+.如果在Uv(g)-mod 有

证明考虑张量积DA(λ)⊗ADA(µ).由特征标的相等得到下面的等式
而Weyl 模的等价类构成了[Uq-mod]的一组基.因此,根据特征标相等,结论成立.证毕.
特别地,下面的张量积分解对于以后的内容很重要,见HONG 等[7]的命题8.6.3.

这样的话,sα,k是以下仿射超平面的反射
并且所有这样的反射生成了仿射Weyl 群Waff.
对于两个权 λ,µ∈X+,如果存在w∈Waff使得
λ=w·µ,那么称它们是相连接的.需要注意的是,这里不是仿射外尔群的“点”作用,因为有ρ-平移.由文献[8]的定理4.3,如果Dq(λ)和Dq(µ)在同一个块,那么λ和μ是相连接的.
下面由LANINI 等[1]给出的同构将 F(DN)和[Uqmod]联系起来.
命题3F(DN) 和[Uq-mod]之间有一个 Q(v)向量空间同构,通过把基向量 λ 映射到 [Dq(λ)].
2 Fock 空间和量子对称对
由于 Z 通过加法作用于 H,考虑剩余类集合H/ℓZ.对 于p∈H (或p∈Z ),用p¯ 表 示 它 在 H/ℓZ(或Z/ℓZ )中的轨道.考虑下面序列的集合
令 F1是基为 SZ的 Q(v) 向量空间,F1/2是基为SH的 Q(v) 向量空间.将 F1和 F1/2简称为Fock 空间.对于F1或 F1/2中的一个元素只有有限多个i≥ 0 使得≠0,只有有限多个i< 0使得=0.因此定义a的charge 为
由charge 为N的序列张成的子空间用和表示,它们被叫做chargeN的Fock 空间.


命 题4映 射 λbλ定 义 了 从 F1/2(DN) 到F1/2,+⊕F1/2,−和从 F1(DN) 到 F1,+⊕F1,−的嵌入.
2.1 基本算子和计数符号
下面的线性算子将在局部改变序列,这是整个构造的基础部分.

定义c为c(i+1/2)−c(i−1/2)=1 并且c(j)=a(j),j≠i±1/2.然后定义


除了这些算子,为了便于书写,定义以下计数符号.
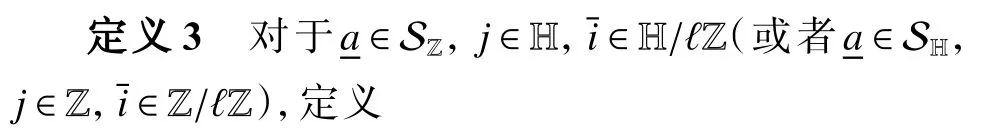
为了简化书写,令
对于a∈SZ,p¯ ∈H/ℓZ (或者a∈SH,p¯ ∈Z/ℓZ),定义
以及

读者可以尝试将ARIKI[9]定义的“杨表”上的作用改写为序列上的作用.这是一个简单的练习,只需要注意有唯一一个序列aϕ可以由aϕ(i)>aϕ(j)推出i 定义4Z/ℓZ (或 H/ℓZ )中的一个元素被称为 下面的定义来自于KOLB[2]. 备注1需要注意的是,Bv(I,Θ)是一个比量子仿射代数复杂得多的对象.有关它的表示论和组合理论远不如量子仿射代数那么好理解. 为了确定移动算子与邻接原理之间的关系,需要介绍一些关于Waff的细节.固定H ={Hβ,m|β ∈Φ+,m∈Z}是所有仿射反射超平面的集合,对于H∈H用sH表示它对应的仿射反射.令表示 H中的所有仿射超平面的补集,的一个连通分支被称为一个开壁室,一个开壁室在中的闭包称作一个壁室. 这样Waff可以作用于壁室.开壁室中的点有平凡的稳定子,而开壁室边界上的点有非平凡的稳定子.每个仿射超平面H∈H定义了两个闭的半空间.对于一个固定的壁室A,用表示包含A的半空间.对于两个壁室A和A′,如果,称超平面H∈H在A和A′之间.这样可以定义两个壁室A和A′之间的距离为 下面是关于仿射Coxeter 群的一个标准结论. 引理1设H∈H 是壁室A和A′之间的一个超平面,那么有d(A,A′) >d(sHA,A′)和d(A,A′) >d(A,sHA′). 对于一个壁室A,与A相交维数最大的仿射超平面的集合 HA被称为A的墙的集合.那么SA={sH|H∈HA}作为一个Coxeter 群,它是Waff的一个生成集.可以发现,对于壁室A和H∈HA,超平面H是A和sHA之间唯一一个超平面.这就引出了下面(最小)通道的概念. 定义6如果存在某个H∈HA使得A′ =sHA,那么这两个壁室A和A′被称为是相邻的.定义一个从A0到Ar的(壁室)通道是一个壁室序列Γ= (A0,A1,A2,···,Ar),其中Ai和Ai+1是相邻的.如果一个通道Γ= (A0,A1,A2,···,Ar)使得r=d(A0,Ar),那么它被叫做是一个最小通道.注意到如果Γ是一个最小通道,那么墙的集合{Hi|Hi在Ai-1和Ai之间}就是A0和Ar之间 的超平面的集合.这些超平面被通道Γ穿过. 由于权可以包含在一个超平面中,因此需要更严格的两个壁室之间的超平面的概念. 定义7对于 λ ∈,用Aλ表示包含λ的一个壁室.对于 λ,µ∈以及包含它们的壁室Aλ和Aμ,如果一个超平面H∈H在Aλ和Aμ之间且H∩{λ,μ} = ∅,那么称它严格的在Aλ和Aμ之间. 在定义7 中,当且仅当λ在Aλ的内部时,包含λ的壁室Aλ是唯一的.下面的引理经常被用来选择一个“好的”通道,它是引理1 的一个推论. 引理2令 λ,µ∈使得λ∈Waffμ.那么可以选择包含它们的壁室Aλ和Aμ,使得从Aλ到Aμ的最小通道只穿过严格的在Aλ和Aμ之间的超平面. 本节研究了移动算子和邻接原理之间的关系.对于本节中接下来的所有内容,固定λ∈X+. 用同样的方法可以证明结论对f-算子也成立.证毕. 与ARIKI[9]中定义的作用不同的是,移动算子可以混合作用.下面引理的证明完全类似于引理3,应用引理2 选择长度为1 的最小通道即可. 接下来考虑r+1 =s的特殊情况,此时对λ ∈X1/2,+与 λ ∈X1,+的结论有所不同. 其他部分与引理5 的证明完全相同.证毕. 对于λ ∈X1/2,+的情况,还需要考虑翻转算子. 同样地,对fr版本的证明方法相同.证毕. 回想一下第2 节定义的移动算子和计数符号,定义如下的线性算子. 引理8令∈H/ℓZ (或者∈Z/ℓZ),那么下面的等式在 F1(或者 F1/2)中成立: 下面说明定义8 中的线性算子满足仿射量子对称对的生成关系. 证明这个结论来自KOLB[2].通过引理8 写出这些算子的表达式,然后考虑KOLB[2]中一个标准量子对称Kac-Moody 对的生成元即可.证毕. 本节将讨论Bv(Z/ℓZ,Θ) (或者Bv(H/ℓZ,Θ))作用与邻接原理的相容性,以及[Uq-mod]中的张量积分解. 命题6令λ∈X½,+,考虑[Uq-mod] 中的张量积分解 其中νi∈X½,+.如果νi和νj是相连接的,那么存在唯一的p¯ ∈ Z/ℓZ 使 得bνi和bνj在 ︿B中具有非0 系数,其中 证明这个结论有两部分.首先,如果[Dq(µ)]在分解式中出现,那么由命题2 可知,存在一个k使得μ=λ+σεk,其中σ∈{±}.除了两种特殊情况,这说明 两个特殊情况是k=N,λN= ±1/2 且λN= −μN,此时有bμ=τbλ.因此,在张量积分解中出现的每个μ都可视作上述算子的和,其中一定有一个算子的系数不为0.根据引理3~5 和7,通过构造,相连接的权可以以相同的算子为加法项构成. 证明利用命题6,对于分解式中出现的每一个[∆q(µ)],bμ作为bλ在移动算子或翻转算子下的像只出现一次,它的系数是v的某个幂次.因此,令v= 1,这就给出了[Uq-mod]中的一个分解.F1/2(DN)在除了f0之外的移动算子和翻转算子下的像都是稳定的.令f0作用于bλ,如果aλ(1/2)=1,结果为0,或者对于a(−1/2)=0 结 果 会 出 现 (a,0) 或 (0,a) ,因 此f0bλ∈C1/2.证毕. 命题7令λ ∈X1,+,考虑[Uq-mod]中的张量积分解 式中νi∈X1,+.如果νi和νj是相连接的,那么存在唯一的∈H/ℓZ使得 ①如果λN> 0,则和在中具有非0系数; ②如果λN< 0,则和在中具有非0系数; ③如果λN= 0,则和在中具有非0系数; 定理3令λ ∈X1,+.对于 µ∈X1,+,存在满足条件 的Laurent 多项式dλ,μ,使得2.2 仿射量子对称对


2.3 仿射量子群
3 移动算子和邻接原理


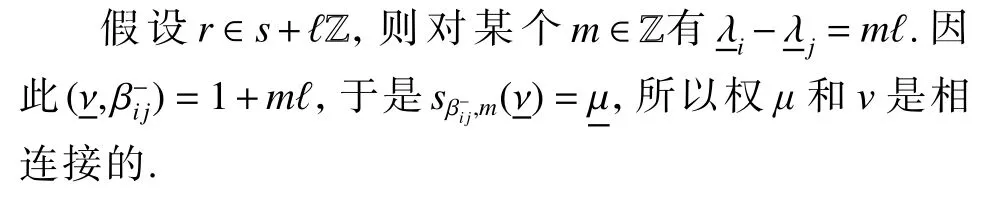








4 仿射量子对称对作用




5 结 论





